El binomio de Newton (teorema del binomio)

En esta página encontrarás la explicación de qué es el binomio de Newton (o teorema del binomio) y cuál es su fórmula. También podrás ver cómo se puede simplificar con el triángulo de Tartaglia (o de Pascal). Además, hallarás ejercicios resueltos paso a paso del binomio de Newton y todas sus propiedades. Finalmente, explicaremos las curiosidades que tiene el origen de este teorema tan peculiar.

¿Qué es el binomio de Newton?

En matemáticas, el binomio de Newton, también conocido como teorema del binomio, es una fórmula que permite calcular de manera fácil la potencia de un binomio. Es decir, el binomio de Newton consiste en una fórmula con la que se pueden resolver expresiones algebraicas de la forma (a+b)n.

Evidentemente, este teorema recibe este nombre en honor al físico, matemático y filósofo Sir Isaac Newton. Sin embargo, existe cierta controversia al respecto ya que se han encontrado textos del Oriente Medio donde ya utilizaban este teorema. Más abajo discutiremos profundamente el origen de esta fórmula matemática.

Fórmula del binomio de Newton

Como hemos visto en la definición del binomio de Newton, este teorema sirve para resolver potencias de binomios. Pero… ¿cómo se aplica el binomio de Newton? O dicho de otra forma, ¿cuál es la fórmula del binomio de Newton?

La fórmula matemática del binomio de Newton es la siguiente:

\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}a^{n-k}b^k

O equivalentemente:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

La fórmula es un poco compleja para entender el concepto del binomio de Newton, así que a continuación hemos hecho las potencias de los binomios de grado más bajo para que puedas comprenderlo mejor:

formula del teorema del binomio de newton

Como puedes ver, al desarrollar cualquier binomio los exponentes del primer término (a) van disminuyendo mientras que los exponentes del segundo término (b) van aumentando, al igual que va incrementando el elemento inferior de los números combinatorios.

Por lo tanto, para utilizar el teorema del binomio debes saber cómo se resuelve un número combinatorio, es decir, la expresión algebraica del tipo \begin{pmatrix} 4 \\ 2 \end{pmatrix}. De modo que antes de ver ejemplos de cómo se calcula un binomio de Newton, vamos a repasar brevemente los números combinatorios.

Número combinatorio

Para determinar un número combinatorio (o coeficiente binomial) se debe aplicar la siguiente fórmula:

\begin{pmatrix}n \\ k \end{pmatrix} = \cfrac{n!}{k!(n-k)!}

Donde n! y k! son números factoriales. Recordemos también que un número factorial se calcula multiplicando todos los números enteros positivos desde 1 hasta dicho número:

n! = 1 \cdot 2 \cdot 3 \cdots (n-1) \cdot n

A modo de ejemplo, vamos a hallar un número combinatorio para que veas cómo se hace:

\begin{pmatrix} 4\\ 3 \end{pmatrix} = \cfrac{4!}{3!(4-3)!}=\cfrac{4!}{3!\cdot 1!}= \cfrac{1 \cdot 2\cdot 3 \cdot 4}{(1 \cdot 2\cdot 3) \cdot 1} = \cfrac{24}{6} = 4

Los números combinatorios también se pueden determinar a través de la calculadora con la tecla \boxed{nCr}.

Ejemplos del binomio de Newton

Ahora que ya sabemos en qué consiste el teorema binomial, vamos a ver cómo aplicar la fórmula del binomio de Newton mediante dos ejemplos numéricos.

Ejemplo 1

  • Aplica el binomio de Newton para calcular la potencia del siguiente binomio:

(x+3)^2

Evidentemente, como este binomio está elevado al cuadrado también se podría resolver con las fórmulas de las identidades notables (cómo resolver identidades notables), pero lo calcularemos con el teorema del binomio a modo de ejemplo.

Primero de todo, tenemos que aplicar la fórmula del binomio de Newton:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

En este caso n=2, por tanto:

\left( x+3\right)^2 =\begin{pmatrix} 2 \\ 0 \end{pmatrix} \right)x^2 \cdot 3^0 + \begin{pmatrix} 2 \\ 1 \end{pmatrix} x^1\cdot3^1 + \begin{pmatrix} 2 \\ 2 \end{pmatrix} x^{0}\cdot3^{2}

Fíjate bien, al principio elevamos el primer término (x) al máximo posible, que en este caso es 2. En cambio, elevamos el segundo término (3) al mínimo posible, que siempre es 0. Pero a medida que vamos avanzando hacia la derecha tenemos que elevar el primer término a un número menos que antes y el segundo término a un número más que antes.

Ahora calculamos los números combinatorios:

\left( x+3\right)^2 =1\cdot x^2\cdot 3^0 + 2\cdot x^1\cdot 3^1 + 1\cdot x^{0}\cdot 3^{2}

Resolvemos las potencias:

\left( x+3\right)^2 =1\cdot x^2\cdot 1 + 2\cdot x\cdot 3 + 1\cdot 1\cdot 9

Y, finalmente, calculamos las multiplicaciones:

\left( x+3\right)^2 =x^2 + 6x + 9

Ejemplo 2

Ahora vamos a solucionar un problema un poco más difícil.

  • Aplica la fórmula del binomio de Newton para hallar la potencia del siguiente binomio:

(2x+1)^3

La fórmula del teorema del binomio es:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

En este caso n=3, por tanto:

\left( 2x+1\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)(2x)^3 \cdot 1^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^{2}\cdot 1^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^{1}\cdot 1^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^{0}\cdot 1^{3}

Calculamos los números combinatorios:

\left( 2x+1\right)^3 =1\cdot (2x)^3 \cdot 1^0 + 3\cdot (2x)^{2}\cdot 1^1 + 3 \cdot (2x)^{1}\cdot 1^{2} + 1\cdot (2x)^{0}\cdot 1^{3}

Ahora resolvemos las potencias, para ello es importante que recuerdes las siguientes dos propiedades:

• Cuando un monomio está elevado a un exponente se eleva al mismo exponente tanto el coeficiente como la variable → (2x)^3=2^3\cdot x^3 =8\cdot x^3 =8x^3

• Cualquier término elevado a 0 da como resultado 1 → (2x)^0=1

Así que encontramos las potencias mediante estas 2 propiedades:

\left( 2x+1\right)^3 =1\cdot 2^3x^3 \cdot 1 + 3\cdot 2^2x^{2}\cdot 1 + 3 \cdot 2^1x^{1}\cdot 1 + 1\cdot 1\cdot 1

\left( 2x+1\right)^3 =1\cdot 8x^3 \cdot 1 + 3\cdot 4x^{2}\cdot 1 + 3 \cdot 2x\cdot 1 + 1\cdot 1\cdot 1

Y, por último, multiplicamos los términos:

\left( 2x+1\right)^3 =8x^3 + 12x^{2}+6x + 1

El binomio de Newton y el triángulo de Tartaglia (o de Pascal)

Como has podido comprobar en los ejemplos de antes, calcular los números combinatorios es un poco tedioso. Por eso te vamos a enseñar un truco para que no tengas que resolver los números combinatorios, ya que se puede saber directamente cuánto valen mediante el triángulo de Tartaglia, también conocido como triángulo de Pascal.

Por si no sabes qué es, el triángulo de Tartaglia, también llamado triángulo de Pascal, se trata de una representación matemática de números ordenados en forma de triángulo.

Para construir el triángulo de Tartaglia o de Pascal debemos empezar con la cúspide del triángulo, que siempre es un 1, y después se van determinando los números de las filas de abajo. Cada número de las filas posteriores es igual a la suma de los dos números que tiene justo encima, excepto los extremos de las filas que siempre son 1.

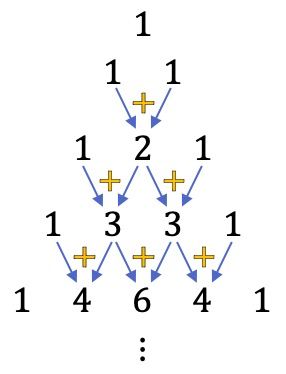
binomio de newton 1 de bachillerato online

Así pues, cada uno de estos números del triángulo de Tartaglia corresponde al resultado de un número combinatorio, fíjate en la siguiente figura:

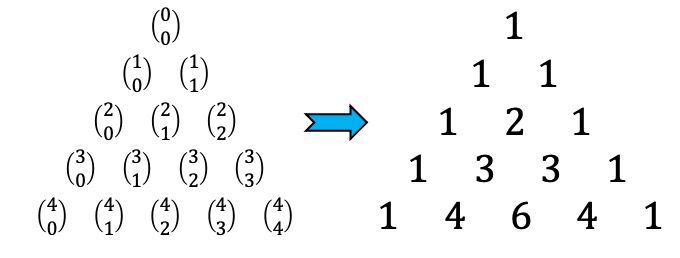
Por ejemplo, el coeficiente binomial \begin{pmatrix} 3 \\ 1 \end{pmatrix} es equivalente a 3, porque en el triángulo de Tartaglia hay un 3 en su posición.

De manera que podemos usar el triángulo de Tartaglia (o de Pascal) para resolver mucho más rápido el binomio de Newton, ya que nos ahorra los cálculos de los números combinatorios.

Por ejemplo, si queremos hacer la siguiente potenciación de un binomio:

(x+5)^3

Al aplicar la regla del binomio de Newton obtenemos la siguiente expresión algebraica:

\left(x+5\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)x^3 \cdot 5^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 5^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 5^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 5^{3}

Pues en lugar de calcular los números combinatorios uno a uno, simplemente podemos sustituir cada número combinatorio por su coeficiente correspondiente del triángulo de Tartaglia. En este caso el binomio está elevado a la 3, por lo que le corresponde el tercer nivel del triángulo:

Triangulo de Tartaglia o de Pascal y binomio de Newton

\left(x+5\right)^3 =\color{red} \bm{1} \color{black} \cdot x^3 \cdot 5^0 + \color{red} \bm{3} \color{black} \cdot x^{2}\cdot 5^1 + \color{red} \bm{3} \color{black} \cdot x^{1}\cdot 5^{2} +\color{red} \bm{1} \color{black} \cdot x^{0}\cdot 5^{3}

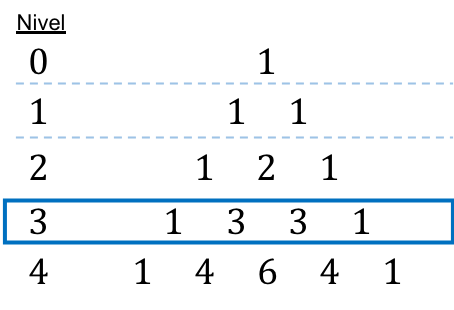
Y ahora solo nos queda hacer las operaciones restantes:

\left(x+5\right)^3 =1 \cdot x^3 \cdot 1 + 3\cdot x^{2}\cdot 5 + 3 \cdot x\cdot 25 +1\cdot 1\cdot 125

\left(x+5\right)^3 =x^3+ 15x^2 + 75x +125

Como puedes ver, el triángulo de Tartaglia (o de Pascal) sirve para calcular el binomio de Newton de una manera más fácil y rápida, tal y como hemos demostrado. Por eso te recomendamos utilizarlo.

Para hacer un resumen de todo lo que hemos visto hasta ahora, te dejamos una imagen en la que se muestra cómo son las expresiones de los binomios de Newton con los números del triángulo de Tartaglia (o de Pascal):

binomio de Newton y triangulo de pascal o de tartaglia

Binomio de Newton negativo: potencia de una resta

Hasta ahora todos los ejemplos del binomio de Newton que hemos resuelto han sido sumas. Por contra, cuando uno de los dos términos del binomio tiene signo negativo, el procedimiento sigue siendo similar pero cambia un poco.

Cuando uno de los términos del binomio sea negativo, es decir se trate de una resta del tipo (a-b)n, se deben alternar los signos del desarrollo del binomio de Newton de la forma + – + – + – + – …

A continuación hemos desarrollado las potencias de binomios negativos de los 5 primeros grados con el teorema del binomio y con los coeficientes del triángulo de Tartaglia ya puestos, para que así puedas hallar directamente la expresión del binomio que necesites:

binomio de newton negativo potencia de una resta 2

Propiedades del binomio de Newton

Las expresiones de binomio de Newton cumplen con las siguientes características:

  • Al desglosar el binomio de Newton siempre se obtiene un término más que el grado del binomio. O dicho con otras palabras, para el binomio (a+b)^n se consiguen n+1 términos.
  • Las potencias del elemento a empiezan con n y van disminuyendo hasta llegar al 0 en el último término.
  • Las potencias del elemento b van a la inversa: empiezan con 0 y van aumentado hasta llegar a n en el último término.
  • Para cada elemento del binomio de Newton, la suma de los exponentes de a y b es igual a n.
  • El coeficiente del primer término de la expresión binomial de Newton siempre es 1 (positivo) y el segundo coeficiente es equivalente al exponente del binomio (positivo o negativo).

Calcular el término k-ésimo del binomio de Newton

Aunque es poco habitual, puede que a veces nos encontremos con problemas en los que en vez de hacer el desarrollo binomial de Newton, nos piden que determinemos el término k-ésimo del binomio de Newton, es decir, el término que ocupa la posición k.

Entonces, para calcular el término que ocupa el lugar k del binomio de Newton se debe emplear una fórmula, que depende de si el binomio es una suma o una resta:

  • Si el binomio de Newton es positivo, el valor del término k-ésimo se calcula con la siguiente fórmula:

(a+b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

  • Si el binomio de Newton es negativo, el valor del término k-ésimo se determina con la siguiente fórmula:

(a-b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

A modo de ejemplo, vamos a hallar el cuarto término del siguiente binomio de grado 5:

(x+3)^5

Como se trata de un binomio compuesto por una suma, aplicamos la primera fórmula:

T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

Sustituimos las variables de la fórmula por sus valores correspondientes:

T_4 = \begin{pmatrix} 5 \\ 4-1 \end{pmatrix} x^{5-4+1}\cdot 3^{4-1}

Y hacemos las operaciones:

T_4 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} x^{2}\cdot 3^{3}

T_4 = 10 \cdot x^{2}\cdot 27

T_4 = 270 x^{2}

Y de esta forma hemos calculado el cuarto término de la expansión binomial de Newton sin necesidad de calcular todos los otros términos.

Ejercicios resueltos del binomio de Newton

Ahora que ya hemos explicado en qué consiste el teorema del binomio, te dejamos con varios ejercicios resueltos paso a paso del binomio Newton para que puedas practicar. Recuerda también que puedes dejarnos las dudas que te surjan o cualquier sugerencia en los comentarios.

Ejercicio 1

Desarrolla la siguiente potencia binomial mediante el teorema del binomio:

(x+4)^3

Primero empleamos la fórmula del binomio de Newton:

\left(x+4\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} x^3 \cdot 4^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 4^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 4^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 4^{3}

Como el binomio está elevado a la 3, nos fijamos en el tercer nivel del triángulo de Tartaglia para hallar directamente los números combinatorios:

teorema del binomio de Newton ejercicios resueltos paso a paso 1 bachillerato

(x+4)^3 = 1\cdot x^3 \cdot 4^0+3 \cdot x^2 \cdot 4^1 + 3 \cdot x^1 \cdot 4^2+1 \cdot x^0 \cdot 4^3

Realizamos las potencias:

1\cdot x^3 \cdot 1 + 3 \cdot x^2 \cdot 4+ 3 \cdot x \cdot 16 +1 \cdot 1 \cdot 64

Y finalmente multiplicamos:

x^3 + 3x^2 \cdot 4 + 3 x \cdot 16 + 64

\bm{x^3 + 12x^2 + 48 x + 64}

 

Ejercicio 2

Calcula la siguiente potencia con la fórmula del binomio de Newton:

(3x+2)^3

En primer lugar, aplicamos la fórmula del binomio de Newton:

\displaystyle \left(3x+2\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} (3x)^3 \cdot 2^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (3x)^{2}\cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (3x)^{1}\cdot 2^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (3x)^{0}\cdot 2^{3}

Como el binomio está elevado al cubo, nos fijamos en el tercer nivel del triángulo de Pascal para averiguar directamente los valores de los números combinatorios:

teorema del binomio de Newton ejercicios resueltos paso a paso 1 bachillerato

\left(3x+2\right)^3 = 1\cdot (3x)^3 \cdot 2^0+3 \cdot (3x)^2 \cdot 2^1+ 3 \cdot (3x)^1 \cdot 2^2+1 \cdot (3x)^0 \cdot 2^3

Calculamos las potencias de monomios:

1\cdot 27x^3 \cdot 1+ 3 \cdot 9x^2 \cdot 2+3 \cdot 3x \cdot 4 + 1 \cdot 1 \cdot 8

Y, para terminar, hacemos las multiplicaciones:

27x^3 + 27x^2 \cdot 2 +9x \cdot 4+8

\bm{27x^3 + 54x^2 +36x+8}

 

Ejercicio 3

Expande la siguiente expresión polinómica mediante la fórmula del binomio de Newton:

(2x-2)^3

Primero de todo, usamos la fórmula del binomio de Newton. Pero como dentro del paréntesis tenemos una resta, tenemos que ir alternando los signos de los coeficientes de cada término:

(2x-2)^3=\begin{pmatrix} 3 \\ 0 \end{pmatrix} (2x)^3 \cdot 2^0-\begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^2 \cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^1 \cdot 2^2-\begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^0 \cdot 2^3

Como el binomio está elevado a la tres, nos fijamos en el tercer nivel del triángulo de Tartaglia para calcular directamente los números combinatorios:

teorema del binomio de Newton ejercicios resueltos paso a paso 1 bachillerato

(2x-2)^3=1\cdot (2x)^3 \cdot 2^0-3 \cdot (2x)^2 \cdot 2^1 + 3 \cdot (2x)^1 \cdot 2^2-1 \cdot (2x)^0 \cdot 2^3

Realizamos las potencias:

1\cdot 8x^3 \cdot 1- 3 \cdot 4 x^2 \cdot 2+ 3 \cdot 2x \cdot 4-1 \cdot 1 \cdot 8

Y resolvemos las multiplicaciones:

8x^3 - 12 x^2 \cdot 2 +6x \cdot 4 -8

\bm{8x^3 -24 x^2 +24x -8}

 

Ejercicio 4

Halla la expresión desarrollada del siguiente binomio de Newton con la fórmula:

(4x-3y)^4

Debemos aplicar la fórmula general del binomio de Newton, pero como en este caso dentro del paréntesis tenemos una resta tenemos que ir alternando los signos de cada término:

\begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}

Como el binomio está elevado a la cuarta, nos fijamos en el nivel 4 del triángulo de Tartaglia para hallar directamente los números combinatorios:

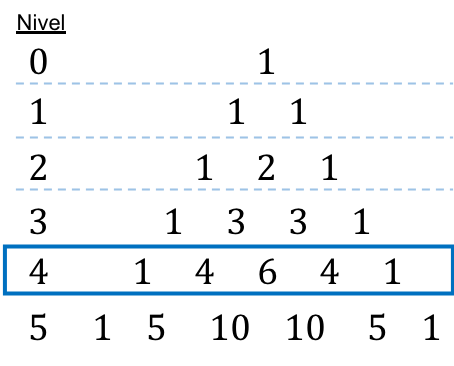
binomio de newton piramide

\begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}

Hacemos todas las potencias:

1\cdot 256x^4 \cdot 1-4\cdot 64x^3 \cdot 3y+6 \cdot 16x^2 \cdot 9y^2 - 4 \cdot 4x \cdot 27y^3+1 \cdot 1 \cdot 81y^4

Y, para acabar, resolvemos las multiplicaciones:

256x^4-256x^3 \cdot 3y+96x^2 \cdot 9y^2 - 16x \cdot 27y^3+81y^4

\bm{256x^4-768x^3y+864x^2y^2-432xy^3+81y^4}

 

Ejercicio 5

Determina el séptimo término del desarrollo de la siguiente expresión binomial:

(2x-5y)^{10}

Como se trata de un binomio negativo, debemos utilizar la siguiente fórmula:

T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

Queremos determinar el término 7 y el binomio está elevado a la 10, por lo tanto al sustituir los valores en la fórmula queda:

T_7= (-1)^{7-1} \begin{pmatrix} 10 \\ 7-1 \end{pmatrix} (2x)^{10-7+1} \cdot (5y)^{7-1}

De modo que solamente nos queda operar para averiguar el término:

\begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}

 

Historia del Binomio de Newton

Aunque el origen del teorema del binomio se le atribuye al célebre científico inglés Isaac Newton (1642-1727), en realidad la primera formulación del teorema la descubrió por primera vez el ingeniero persa Al-Karijí alrededor del año 1000. E incluso se ha descubierto que durante el siglo XIII los matemáticos chinos Yang Hui y Chuh Shih-Chieh ya conocían las expansiones binomiales de grados pequeños.

Más tarde, durante el siglo XVII, Newton aprovechó las bases establecidas por los matemáticos anteriores para expandir el teorema del binomio. Utilizando los métodos de interpolación y extrapolación del matemático John Walls y conceptos de exponentes generalizados, consiguió transformar una expresión polinómica en una serie infinita.

Hacía el año 1665, Newton logró demostrar que el exponente n del teorema del binomio también podía ser un exponente racional, es decir, la potencia de un binomio también se puede solucionar si el exponente es una fracción. Por otro lado, también hizo la demostración para el caso de un exponente negativo. Y, sorprendentemente, encontró que los desarrollos de ambas expresiones son series infinitas de términos.

Fue con este hallazgo que Newton empezó a cuestionarse la relación entre las series infinitas y las expresiones polinómicas finitas, y dedujo que que matemáticamente se pueden hacer operaciones con series infinitas de manera similar a las expresiones polinómicas finitas. Aunque Newton nunca publicó este teorema, lo acabó haciendo John Walls en 1685 otorgando dicho descubrimiento a Newton.

12 comentarios en “El binomio de Newton (teorema del binomio)”

    1. Polinomios

      Hola Alondra,

      Me alegro de que te haya gustado el artículo, sin embargo, no sé a qué concepto te refieres con el monomio de newton. Pero por si te interesa y está relacionado, puedes consultar cómo se calcula la potencia de un monomio buscando el artículo en nuestra página web.

  5. Alfonso

    Pregunta cómo se calcula el cuadrado, cubo, etc., de un binomio en que el primer elemento de dicho binomio sea negativo?. Ejemplo (-5a+3b) o (-2x-5y)

    Responder
    1. Polinomios

      Hola Alfonso,

      Simplemente debes incluir el negativo en el cuadrado, cubo, etc. Por ejemplo:

      \left(-2x\right)^2=(-2)^2\cdot x^2=4x^2

      \left(-2x\right)^3=(-2)^3\cdot x^3=-8x^3

    2. Juan

      Excelente explicación.
      Una acotación:
      Amigos, en la segunda pregunta consultada aquí (-2X)^3, el resultado es -8X^3 (les falta indicar el signo negativo)
      Saludos!

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio