▷ Cómo factorizar cualquier tipo de polinomio ✅ (ejercicios resueltos)

En esta página explicamos cómo factorizar cualquier tipo de polinomio. Primero veremos cómo se hace la factorización de un polinomio con la regla de Ruffini, seguidamente pasaremos a cómo se factorizan polinomios sin término independiente, luego analizaremos las factorizaciones de polinomios de raíces con fracciones y, finalmente, los casos especiales de factorizaciones (identidades notables, factorización por agrupación, trinomios, etc.). Todas las explicaciones están hechas con ejemplos y, además, al final podrás practicar con los ejercicios resueltos paso a paso de factorizar polinomios.

Índice

¿Qué es la factorización de polinomios?

La factorización de polinomios es una técnica que se utiliza en matemáticas para descomponer un polinomio en el producto de factores.

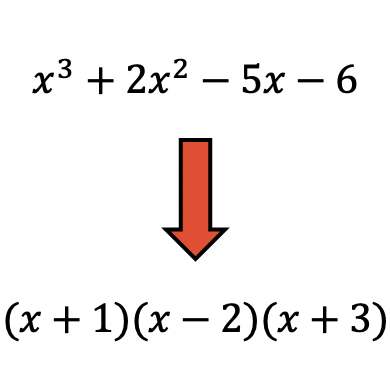
factorizacion de polinomios (factorizar polinomios)

La factorización de polinomios resulta muy útil ya que es más fácil hacer operaciones con polinomios factorizados.

Ahora que ya sabemos en qué consiste la factorización de polinomios, veamos cómo se factorizan los polinomios.

Cómo factorizar polinomios con la regla de Ruffini

Evidentemente, para poder entender cómo se factoriza un polinomio con la regla de Ruffini, primero debes saber cómo aplicar la regla de Ruffini. Así que te dejamos este enlace por si primero quieres repasar cómo era el procedimiento.

Para factorizar un polinomio se deben seguir los siguientes pasos:

Se calculan las raíces del polinomio con la regla de Ruffini.
Se expresa cada raíz hallada del tipo x=a en forma de factor (x-a).
El polinomio factorizado es el producto de todos los factores encontrados multiplicados por el coeficiente del término de mayor grado del polinomio sin factorizar.

Para que puedas ver cómo se hace y entender mejor el procedimiento de la factorización de polinomios, a continuación tienes un ejemplo resuelto explicado paso a paso:

Descompone factorialmente el siguiente polinomio:

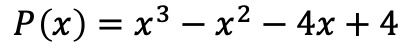
Lo primero que debemos hacer es calcular las raíces o ceros del polinomio. Para ello, tenemos que hallar los divisores del término independiente del polinomio, que en este caso son ±1, ±2 y ±4.

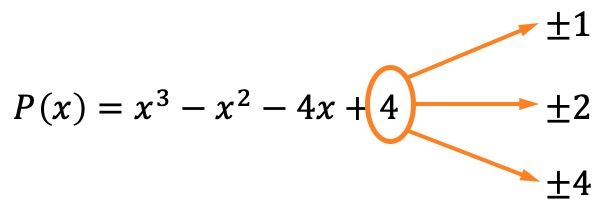
Ahora sabemos, por el teorema del resto y del factor, que si el resto de la división del polinomio entre uno de estos valores es igual a 0, significa que dicho valor es una raíz del polinomio.

Por lo tanto, tenemos que dividir el polinomio entre cada uno de los divisores del término independiente con la regla de Ruffini y ver en qué casos el resto es nulo.

Empezamos, por ejemplo, aplicando la regla de Ruffini con $x=+1:$

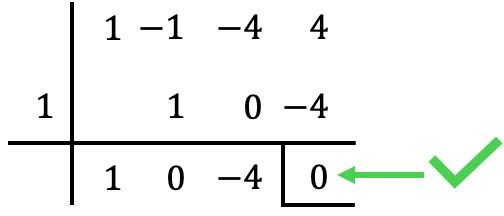
En este caso el resto (o residuo) de la división es cero, por lo que $x=1$ es una raíz del polinomio. ✅

Perfecto, ya tenemos una raíz del polinomio, ahora solo nos queda determinar las otras raíces restantes. Para ello, utilizamos la regla de Ruffini con otro divisor del término independiente, por ejemplo $x=-1.$ Además, no es necesario usar el método de Ruffini con todo el polinomio, sino que podemos continuar desde donde lo hemos dejado en el paso anterior:

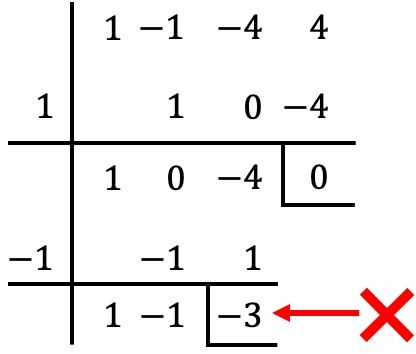
Sin embargo, en este caso cuando dividimos entre $x=-1$ el resto obtenido es diferente de 0, así que $x=-1$ no es una raíz del polinomio. ❌

De modo que debemos probar con otro valor, por ejemplo hacemos la regla de Ruffini con $x=+2:$

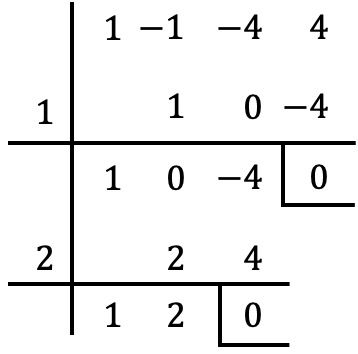
En este caso volvemos a conseguir un resto nulo, por tanto, $x=2$ también es una raíz del polinomio.

Y seguimos aplicando el mismo procedimiento. Ahora comprobamos si $x=-2$ es una raíz del polinomio o no:

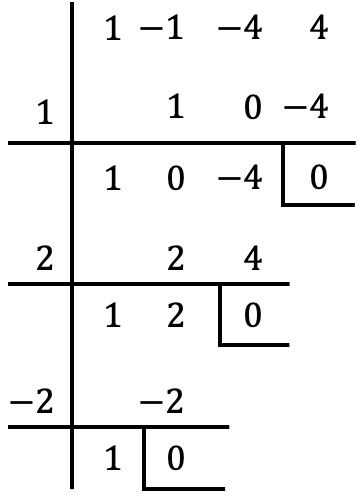
Al dividir entre $x=-2$ con la regla de Ruffini obtenemos un resto nulo, con lo que $x=-2$ es una raíz o cero del polinomio.

De forma que ya no podemos seguir aplicando la regla de Ruffini, por tanto, ya hemos encontrado todas las raíces del polinomio, que son:

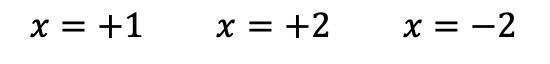
Una vez hemos determinado todas las raíces del polinomio, ya podemos factorizarlo. Para ello simplemente debemos expresar cada raíz $x=a$ en forma de factor del tipo $(x-a)$ , es decir, por cada raíz debemos poner un paréntesis con una $x$ y la raíz cambiada de signo:

Y ahora que ya tenemos todas raíces expresadas en forma de factores, tenemos que multiplicar todos los paréntesis por el coeficiente del término de mayor grado del polinomio original:

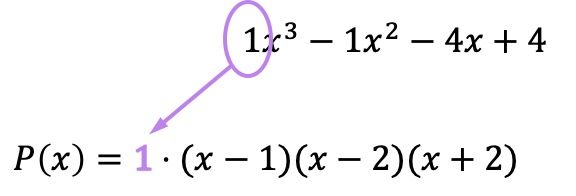
factorizar polinomios coeficiente mayor grado

Aunque en este caso el coeficiente es 1 y por tanto no afecta al resultado, es importante acordarse de hacer esta multiplicación. Ya que si dicho coeficiente fuese distinto de 1 el polinomio factorizado cambiaria y, en consecuencia, al no poner el número estaríamos cometiendo un error en la factorización del polinomio.

En definitiva, el polinomio factorizado es:

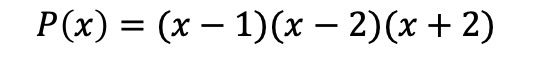
Factorizar polinomios sin término independiente

Acabamos de ver que el término independiente es importante para la factorización de polinomios, ya que nos permite identificar las posibles raíces del polinomio. Sin embargo, ¿cómo factorizamos un polinomio que no tiene término independiente?

Para factorizar un polinomio sin término independiente, primero tenemos que extraer factor común del polinomio, y luego debemos sacar las raíces del polinomio sin el factor en común mediante la regla de Ruffini.

Así escrito puede parecer un poco complicado, por lo que vamos a resolver un ejemplo paso a paso para que puedas ver cómo se hace la factorización de un polinomio con factor común:

Realiza la descomposición factorial del siguiente polinomio:

$P(x) = x^4-3x^3-x^2+3x$

Como puedes ver, el polinomio del problema no tiene término independiente, de modo que debemos sacar factor común del polinomio. Si nos fijamos bien, todos los elementos del polinomio tienen como mínimo una $x,$ así que el factor en común es la $x.$ Por lo tanto, al extraer factor común del polinomio nos queda la siguiente expresión:

$P(x) = x\left(x^3-3x^2-x+3\right)$

Y una vez hemos extraído factor común del polinomio, aplicamos la regla de Ruffini para calcular las raíces del polinomio agrupado en el paréntesis (con el procedimiento que hemos visto en el apartado anterior):

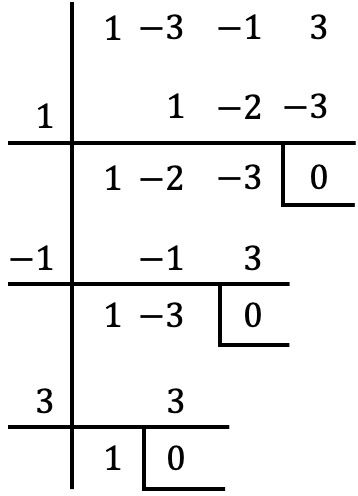
factorizar polinomios sin termino independiente

De manera que las raíces o ceros del polinomio de dentro del paréntesis son:

$\bm{x=+1 \qquad x=-1 \qquad x=+3}$

Por tanto, para factorizar el polinomio simplemente tenemos que sustituir el polinomio de dentro del paréntesis por sus raíces en forma de factores (tal y como se ha explicado en el apartado de arriba):

$\begin{array}{c}P(x) = x\left(x^3-3x^2-x+3\right) \\[2ex]\color{red} \bm{\downarrow} \\[2ex] \bm{P(x) = x(x-1)(x+1)(x-3)}\end{array}$

Y de esta forma ya hemos factorizado el polinomio que no tenía término de grado 0. Fíjate que la única diferencia es que primero debemos extraer factor común, pero todos los siguientes pasos son exactamente idénticos.

Por otro lado, debes saber que $x=0$ también es una raíz del polinomio, ya que cuando extraemos factor común implica que una de las raíces del polinomio es $x=0.$ Entonces, todas las raíces del polinomio son las siguientes:

$\bm{x= 0 \qquad x=+1 \qquad x=-1 \qquad x=+3}$

De hecho, el polinomio debe tener tantas raíces como indica su grado. En este caso el polinomio es de grado 4 y por eso tiene 4 raíces.

Factorizar polinomios con raíces racionales

Hasta ahora hemos visto ejemplos de factorizaciones de polinomios con raíces enteras, sin embargo, un polinomio también puede tener raíces racionales, es decir, con fracciones. Veamos cómo se resuelven este tipo de factorizaciones polinómicas con un ejemplo:

Factoriza el siguiente polinomio incompleto:

$P(x) = 4x^3-7x+3$

Como siempre, utilizamos la regla de Ruffini con los divisores del término independiente para intentar determinar las raíces del polinomio:

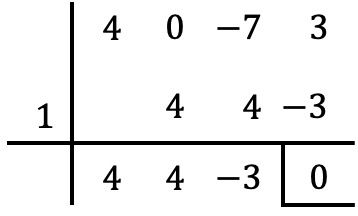
factorizacion de polinomios con raices racionales

Pero no podemos calcular más raíces con Ruffini, ya que si probamos de hacer Ruffini con todos los otros números que son divisores del término independiente obtenemos un resto distinto de cero.

De modo que nos encontramos en la situación de que solamente con $x=1$ el resto de la división es equivalente a 0, esto significa que el polinomio puede tener raíces fraccionales. Para determinar dichas raíces podríamos aplicar Ruffini con fracciones, sin embargo, es muy fácil equivocarse en los cálculos y por eso en estos caso se suele hacer lo siguiente:

Cuando no podemos seguir aplicando la regla de Ruffini con raíces enteras, tenemos que igualar el último polinomio obtenido a 0 y resolver la ecuación resultante. De manera que las raíces del polinomio serán los valores hallados de la ecuación.

Por contra, si la ecuación no tiene solución quiere decir que el polinomio no tiene más raíces y, en consecuencia, no es factorizable completamente.

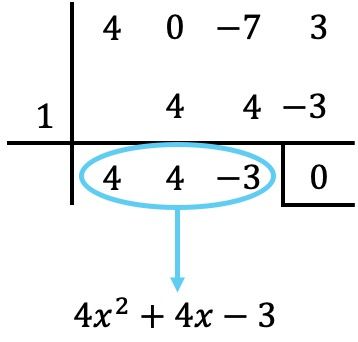
Así que igualamos el polinomio del cociente a cero:

$4x^2+4x-3=0$

Y utilizamos la fórmula de la ecuación de segundo grado para resolver la ecuación resultante:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-4 \pm \sqrt{4^2-4\cdot 4\cdot (-3)}}{2\cdot 4}= \cfrac{-4\pm \sqrt{16+48}}{8} = \cfrac{-4 \pm\sqrt{64}}{8}$

$\displaystyle x = \cfrac{-4 \pm 8}{8} = \begin{cases} \cfrac{-4+8}{8} = \cfrac{4}{8} = \cfrac{1}{2} \\[4ex]\cfrac{-4-8}{8} = \cfrac{-12}{8} = -\cfrac{3}{2} \end{cases}$

Por lo tanto, las raíces del polinomio son:

$x=+1 \qquad x=\cfrac{1}{2} \qquad x=-\cfrac{3}{2}$

De modo que el polinomio tiene raíces en forma de fracciones.

Y una vez ya sabemos todas las raíces del polinomio, podemos averiguar el polinomio factorizado fácilmente expresando cada raíz $x=a$ en forma de factor del tipo $(x-a)$ , es decir, por cada raíz debemos poner un paréntesis con una $x$ y la raíz cambiada de signo:

$\displaystyle P(x)= 4\left(x-1\right)\left(x-\frac{1}{2}\right)\left(x+\frac{3}{2}\right)$

Recuerda que para factorizar un polinomio también se deben multiplicar sus factores por el coeficiente del término de mayor grado del polinomio sin factorizar, que en este caso es 4.

Casos especiales de la factorización de polinomios

Normalmente para factorizar un polinomio se utiliza la regla de Ruffini (o división sintética), tal y como se ha explicado arriba. Pero dependiendo del polinomio del problema, a veces se puede hacer la factorización polinómica más rápidamente. A continuación vamos a ver cada uno de estos caso peculiares.

Factorización de identidades notables

Si vemos que un polinomio corresponde a una identidad notable (o producto notable) es muy sencillo factorizarlo. Sin embargo, para poderlo hacer debes dominar las fórmulas de las identidades notables, de lo contrario te recomiendo que le eches un vistazo a este enlace donde no solo encontrarás las fórmulas, sino que además podrás ver ejemplos de las identidades notables e incluso podrás practicar con ejercicios resueltos paso a paso.

Diferencia de cuadrados

Como bien sabes, la fórmula de la identidad notable de la diferencia de cuadrados es la siguiente:

$a^2-b^2=(a+b)\cdot (a-b)$

Por lo tanto, si encontramos con polinomio que cumpla con la expresión $a^2-b^2$ se puede factorizar directamente.

Fíjate en el siguiente ejemplo en el que se factoriza una diferencia de cuadrados:

$x^2-9 = (x+3)(x-3)$

Por otra parte, las raíces del polinomio son:

$x=-3 \qquad x=+3$

Más ejemplos de la factorización de binomios que son diferencias de cuadrados:

$x^2-4=(x+2)(x-2) \quad \longrightarrow \quad \text{ra\'ices: } x=-2, +2$

$x^2-16=(x+4)(x-4) \quad \longrightarrow \quad \text{ra\'ices: } x=-4, +4$

$x^2-25=(x+5)(x-5) \quad \longrightarrow \quad \text{ra\'ices: } x=-5, +5$

Cuadrado de la suma y de la resta

Ya debes conocer las fórmulas de las 2 identidades notables principales restantes: el cuadrado de la suma y el cuadrado de la resta.

Cuadrado de la suma

$a^2+2ab+b^2 = (a+b)^2$

Cuadrado de la resta

$a^2-2ab+b^2= (a-b)^2$

Así pues, si nos damos cuenta que un polinomio corresponde a una de estas dos identidades notables, lo podemos factorizar directamente. Fíjate en los siguientes ejemplos:

$x^2+6x+9 = (x+3)^2$

Raíz doble: $x=-3$

$x^2-8x+16 = (x-4)^2$

Raíz doble: $x=4$

Identificar este tipo de productos notables es un poco más difícil. Un truco es comprobar si el término independiente del polinomio es el cuadrado de algún número, y si el término de mayor grado es el cuadrado de algún monomio (normalmente $x$ ), en tal caso, solo nos queda verificar que se cumple que $2ab$ es igual al término de grado intermedio.

Por ejemplo, si tenemos el siguiente polinomio:

$x^2+10x+25$

En este caso solo puede ser el cuadrado de una suma, porque todos los elementos del polinomio son positivos. Entonces, la variable $b$ de la fórmula debe de ser 5, ya que es la raíz del término independiente, y la variable $a$ tiene que ser $x$ , ya que es la raíz del término de mayo grado.

$a=\sqrt{x^2} = x$

$b=\sqrt{25} = 5$

Así que ahora solo nos queda demostrar que se cumple la fórmula del cuadrado de la suma con el término de grado intermedio:

$2ab = 10x \ \color{blue} \bm{?}$

$2ab = 2\cdot x \cdot 5 = 10 x$ ✅

La fórmula del producto notable se cumple, por lo tanto, el polinomio factorizado es:

$x^2+10x+25 = (x+5)^2$

Y la raíz de este polinomio es $x=-5,$ que es una raíz doble porque su factor está elevado al cuadrado (se repite dos veces).

Seguidamente tienes más ejemplos de la factorización de trinomios cuadrados perfectos:

$x^2-4x+4=(x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+2$

$x^2+14x+49=(x+7)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=-7$

$9x^2-12x+4=(3x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+\cfrac{2}{3}$

Factorización de trinomios de segundo grado

Como acabamos de ver, a veces hay trinomios que son cuadrados perfectos y estos se pueden factorizar de manera directa con las fórmulas de las identidades notables. Pero la mayoría de trinomios no son productos notables, por tanto, ¿cómo se hace la factorización de estos casos de polinomios?

Para factorizar un polinomio de segundo grado no hace falta aplicar el método de Ruffini, simplemente se iguala el polinomio a cero y se resuelve la ecuación de segundo grado resultante. De modo que las soluciones de la ecuación serán las raíces del polinomio.

Por ejemplo, si nos piden de factorizar el siguiente polinomio de grado 2:

$P(x) = x^2+2x-15$

En vez de utilizar Ruffini, igualamos el polinomio a 0:

$x^2+2x-15=0$

Y ahora usamos la fórmula de la ecuación de 2º grado para hallar las soluciones de la ecuación:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-2 \pm \sqrt{2^2-4\cdot 1\cdot (-15)}}{2\cdot 1}= \cfrac{-2\pm \sqrt{4+60}}{2} = \cfrac{-2 \pm\sqrt{64}}{2}$

$\displaystyle x = \cfrac{-2 \pm 8}{2} = \begin{cases} \cfrac{-2+8}{2} = \cfrac{6}{2} = 3 \\[4ex]\cfrac{-2-8}{2} = \cfrac{-10}{2} = -5 \end{cases}$

De manera que las raíces del polinomio son:

$x=3 \qquad x=-5$

Y, finalmente, la factorización polinomial es:

$P(x) =(x-3)(x+5)$

Factorización de trinomios de cuarto grado con exponentes pares

Al igual que en el caso anterior, para factorizar un polinomio de cuarto grado con exponentes pares debemos igualar el polinomio a cero y resolver la ecuación bicuadrada. De forma que los valores hallados corresponderán a las raíces del polinomio.

A modo de ejemplo, vamos a factorizar el siguiente polinomio de grado 4:

$P(x) =x^4-5x^2+4$

En primer lugar, igualamos el polinomio a cero:

$x^4-5x^2+4=0$

Ahora tenemos que resolver la ecuación bicuadrada. Para ello, hacemos un cambio de variable:

$x^2=t$

$t^2-5t+4=0$

Resolvemos la ecuación de segundo grado con la fórmula:

$t= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$t= \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1}= \cfrac{5\pm \sqrt{25-16}}{2} = \cfrac{5 \pm\sqrt{9}}{2}$

$\displaystyle t = \cfrac{5 \pm 3}{2} = \begin{cases} \cfrac{5+3}{2} = \cfrac{8}{2} = 4 \\[4ex]\cfrac{5-3}{2} = \cfrac{2}{2} = 1 \end{cases}$

Deshacemos el cambio de variable para calcular las raíces:

$x^2=t$

$x^2=4$

$x=\sqrt{4}$

$x=\pm 2$

$x^2=1$

$x=\sqrt{1}$

$x=\pm 1$

Por lo tanto, las raíces del polinomio son:

$x=+2 \qquad x=-2 \qquad x=+1 \qquad x=-1$

Y una vez sabemos las raíces o ceros del polinomio, lo factorizamos expresando sus raíces algebraicamente en forma de factores:

$P(x) =(x-1)(x+1)(x-2)(x+2)$

Factorización de polinomios por agrupación

En algunos casos muy concretos, se puede utilizar una fórmula para factorizar un tipo de polinomio muy particular.

Si tenemos un polinomio de la siguiente forma:

$x^2-ax- bx+ab$

Podemos simplificar el polinomio sacando factor común:

$x^2-ax- bx+ab = x(x-a)-b(x-a)$

Y aún se puede simplificar más el polinomio extrayendo factor común por segunda vez:

$x(x-a)-b(x-a) =(x-a)\cdot (x-b)$

De esta forma hemos podido factorizar el polinomio sin aplicar Ruffini ni cualquier otro método. Y las raíces de dicho polinomio serían:

$x=a \qquad x=b$

Veamos ahora este método con un ejemplo numérico:

$x^2-3x-2x+6$

Primero de todo sacamos factor común con $x$ y con 2:

$x^2-3x-2x+6 = x(x-3)-2(x-3)$

Y como ahora $(x-3)$ es un factor común del polinomio, extraemos factor común de $(x-3):$

$x(x-3)-2(x-3)=(x-3)\cdot (x-2)$

Por tanto las raíces del polinomio son:

$x=3 \qquad x=2$

Este método también se llama factorización de polinomios por doble extracción de factor común. Aunque es un procedimiento muy rápido, nosotros no recomendamos hacer este tipo de factorización porque frecuentemente se comenten fallos factorizando con este método. Además, como hemos visto más arriba, un polinomio de grado 2 también se puede factorizar resolviendo una simple ecuación cuadrática. En definitiva, no pasa nada si no entiendes del todo este método.

Por último, cabe destacar que aún existen otros métodos de factorización de polinomios más complejos, como por ejemplo el algoritmo LLL, el método de Kronecker y el método de Trager, que aquí no se explican debido a su dificultad matemática.

Ejercicios resueltos de factorización de polinomios

Una vez has visto todos los tipos de factorización de polinomios, te recomendamos que practiques intentando resolver ejercicios. Por eso a continuación te hemos preparado varios ejercicios resueltos paso a paso de factorizar polinomios. Recuerda que si te surge alguna duda puedes escribirla en los comentarios, que la contestaremos rápidamente.

Ejercicio 1

Realiza la factorización del siguiente polinomio de grado 3:

$P(x)=x^3-3x^2-6x+8$

Ver solución

Se trata de un polinomio completo, ordenado, de tercer grado y con término independiente. Por tanto, aplicamos el método de Ruffini para determinar las raíces del polinomio:

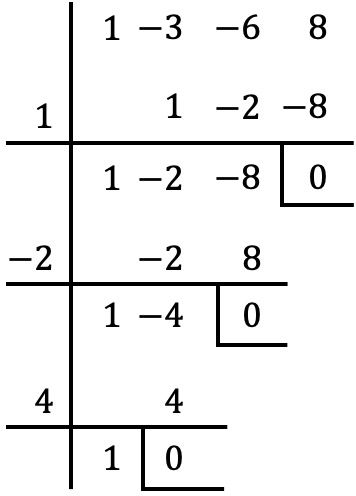
ejercicios resueltos paso a paso de factorizacion de polinomios

De manera que las raíces del polinomio son las siguientes:

$x=+1 \qquad x=-2 \qquad x=+4$

Así que la factorización polinómica es:

$P(x)= 1 \cdot (x-1)\cdot (x+2) \cdot (x-4)$

$\bm{P(x)= (x-1)(x+2)(x-4)}$

Ejercicio 2

Calcula la factorización del siguiente polinomio de grado 4:

$P(x)=x^4+x^3-7x^2-x+6$

Ver solución

Se trata de un polinomio de cuarto grado y con término independiente, por lo que utilizamos el método de Ruffini para hallar las raíces del polinomio:

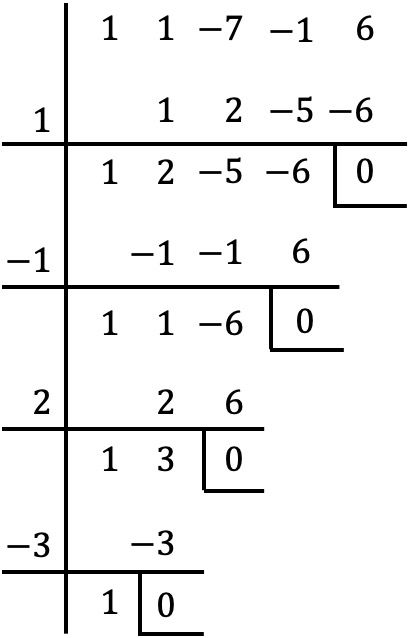
ejercicios de factorizacion de polinomios pdf

De modo que las raíces del polinomio consisten en:

$x=+1 \qquad x=-1 \qquad x=2 \qquad x=-3$

Y cuando factorizamos el polinomio nos queda:

$P(x)= 1 \cdot (x-1)\cdot (x+1)\cdot (x-2) \cdot (x+3)$

$\bm{P(x)= (x-1)(x+1)(x-2)(x+3)}$

Ejercicio 3

Halla la factorización del siguiente polinomio de cuarto grado:

$P(x)=x^4-2x^3-13x^2-10x$

Ver solución

En este caso el polinomio no tiene término independiente, de forma que primero debemos extraer factor común:

$P(x)=x(x^3-2x^2-13x-10)$

Ahora que ya hemos sacado factor común de x, calculamos las raíces o ceros del polinomio de dentro del paréntesis mediante el método de Ruffini:

factorización de polinomios ruffini ejercicios resueltos pdf

De manera que las raíces del polinomio son las que hemos encontrado por el método de Ruffini más x=0 del factor común:

$x=0 \qquad x=-1 \qquad x=-2 \qquad x=5$

Y, por último, al descomponer el polinomio en factores obtenemos la siguiente expresión:

$P(x)= 1 \cdot x \cdot (x+1)\cdot (x+2)\cdot (x-5)$

$\bm{P(x)= x(x+1)(x+2)(x-5)}$

Ejercicio 4

Transforma en factores el siguiente polinomio de tercer grado:

$P(x)=6x^3+25x^2+21x-10$

Ver solución

Este polinomio sí que posee término independiente, así que calculamos sus raíces con el algoritmo de Ruffini:

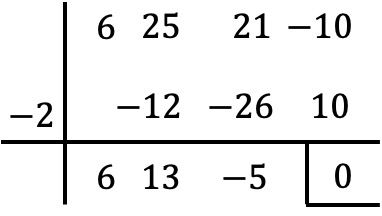
factorizar polinomios de grado 3 online 2

Sin embargo, cuando llegamos a este punto no podemos seguir procediendo con la regla de Ruffini, ya que con ningún otro número entero el resto de la división es nulo.

Por tanto, igualamos el polinomio obtenido a cero:

$6x^2+13x-5=0$

Y aplicamos la fórmula de las ecuaciones cuadráticas para resolver la ecuación resultante:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-13 \pm \sqrt{13^2-4\cdot 6\cdot (-5)}}{2\cdot 6}= \cfrac{-13\pm \sqrt{169+120}}{12} = \cfrac{-13 \pm\sqrt{289}}{12}$

$\displaystyle x = \cfrac{-13 \pm 17}{12} = \begin{cases} \cfrac{-13+17}{12} = \cfrac{4}{12} = \cfrac{1}{3} \\[4ex]\cfrac{-13-17}{12} = \cfrac{-30}{12} = -\cfrac{5}{2} \end{cases}$

De modo que las raíces o ceros del polinomio son:

$x=-2 \qquad x=\cfrac{1}{3} \qquad x=-\cfrac{5}{2}$

Por lo que la factorización del polinomio se debe de hacer con fracciones:

$\displaystyle P(x)= 6\left(x+2\right)\left(x-\frac{1}{3}\right)\left(x+\frac{5}{2}\right)$

Ejercicio 5

Determina la factorización del siguiente polinomio de grado 6:

$P(x)=x^6-3x^5+14x^3-12x^2$

Ver solución

El polinomio del problema no tiene término independiente así que primero debemos extraer factor común, que en este caso es $x^2:$

$P(x)=x^2(x^4-3x^3+14x-12)$

Y una vez hemos sacado factor común del polinomio, hallamos las raíces del polinomio de dentro del paréntesis a través de la regla de Ruffini:

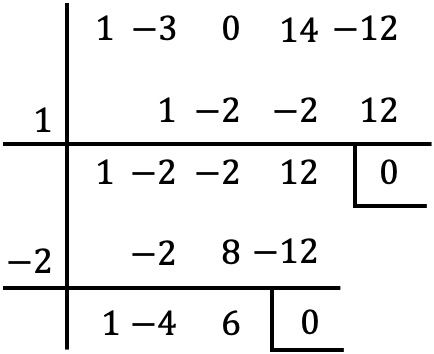
Pero cuando llegamos a este paso no podemos seguir avanzando, porque con ningún otro número entero el resto es igual a cero.

De modo que igualamos el polinomio obtenido a cero:

$x^2-4x+6=0$

Y resolvemos la ecuación de segundo grado con la fórmula:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1\cdot 6}}{2\cdot 1}= \cfrac{4\pm \sqrt{16-24}}{2} = \cfrac{4 \pm\sqrt{-8}}{2} \ \color{red} \bm{\times}$

No existen las raíces de números negativos por tanto la ecuación no tiene solución, cosa que significa que no podemos encontrar más raíces del polinomio. Es decir, el polinomio no es factorizable totalmente.

Sin embargo, las raíces que sí que hemos podido encontrar son:

$x=0 \qquad x=0 \qquad x=1 \qquad x=-2$

Fíjate que la raíz $x=0$ está repetida dos veces porque hemos sacado el factor en común de $x^2,$ y como está elevado al cuadrado implica que es una raíz doble.

En conclusión, el polinomio factorizado será el producto de todas las raíces halladas expresadas en forma de factores $(x-a)$ multiplicadas por el polinomio obtenido de la regla de Ruffini que no se ha podido factorizar más:

$P(x)= 1 \cdot x^2 \cdot (x-1)\cdot (x+2)\cdot (x^2-4x+6)$

$\bm{P(x)= x^2(x-1)(x+2)(x^2-4x+6)}$

Ejercicio 6

Realiza las factorizaciones de todos los siguientes polinomios:

$\text{A)} \ P(x)=x^2 + 12x+36$

$\text{B)} \ Q(x)=x^2 -64$

$\text{C)} \ R(x)=x^2 - 18x+81$

$\text{D)} \ S(x)=x^2+10x+24$

Ver solución

El polinomio del apartado A) corresponde a una identidad notable, concretamente al cuadrado de la suma. Así que su factorización es:

$P(x)=x^2 + 12x+36 = \bm{(x+6)^2}$

El polinomio del apartado B) también es un producto notable, en particular se trata de la diferencia de cuadrados, por tanto:

$Q(x)=x^2 -64 = \bm{(x+8)(x-8)}$

Del mismo modo, el polinomio del apartado C) es una igualdad notable, concretamente consiste en el cuadrado de una resta. De modo que su factorización es:

$R(x)=x^2 - 18x+81 = \bm{(x-9)^2}$

Para terminar, el polinomio del apartado D) no es ninguna identidad notable. Por lo que debemos igualar el polinomio a 0 y solucionar la ecuación resultante para hallar sus raíces:

$x^2+10x+24 =0$

Utilizamos la fórmula de la ecuación de segundo grado:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-10 \pm \sqrt{10^2-4\cdot 1\cdot 24}}{2\cdot 1}= \cfrac{-10\pm \sqrt{100-96}}{2} = \cfrac{-10 \pm\sqrt{4}}{2}$

$\displaystyle x = \cfrac{-10 \pm 2}{2} = \begin{cases} \cfrac{-10+2}{2} = \cfrac{-8}{2} = -4 \\[4ex]\cfrac{-10-2}{2} = \cfrac{-12}{2} = -6\end{cases}$

De manera que las raíces del polinomio D) son:

$x=-4 \qquad x=-6$

Y, finalmente, el resultado de la factorización polinómica es:

$\bm{S(x)=(x+4)(x+6)}$

11 comentarios en “Cómo factorizar polinomios (factorización de polinomios)”

Alicia
25/04/2021 a las 19:50

Cómo puedo factorizar un polinomio de grado 3 que no tiene raíces racionales? Gracias!!

Responder
1. Polinomios
  29/04/2021 a las 14:17
  
  Hola Alicia,
  
  Si el polinomio no tiene raíces racionales, significa que tendrá raíces complejas. En tal caso, debes igualar el polinomio a cero y resolver la ecuación cúbica resultante. Entonces simplemente debes factorizar el polinomio de tercer grado con las raíces complejas obtenidas, es decir, cambiándolas de signo y poniéndolas en forma de productos de factores.
confusa
19/06/2021 a las 20:30

Hola muy buenas, me gustaría saber si en polinomios con más de una variable se puede aplicar ruffini, teorema del resto o algún otro método.
Por otro lado, me gustaría decir que por el teorema del resto, sustituyendo en el polinomio inicial la incógnita por las posibles raíces y operando, se puede saber de una manera más sencilla que con ruffini, cuáles son las raíces.

Por ejemplo, polinomio a factorizar; x²+2x+4
Posibles raíces: los divisores de 4 (1,2,4,-1,-2,-4)
Sustituyendo la incógnita del polinomio inicial por las posibles raíces:
(-1)²+2(-1)+4=1-2+4=3
Como el resto no es cero, -1 no es raíz.
Y de esa forma se va comprobando, al igual que con ruffini, con todas las posibles raices, pero creo que esta manera es más sencilla.

Ruffini sin embargo es fundamental para conocer los coeficientes en los casos de los polinomios irreductibles. Me refiero:
En el polinomio x³-x-6, con el teorema del resto averiguo que 2 es raíz y que no tengo ninguna otra más, por lo que la factorización debe ser (x-2) por (polinomio irreductible). Aplicando ruffini con la raíz que hallé gracias al teorema del resto, se obtiene como producto final el polinomio irreductible y de esa manera se termina la factorización:
x³-x-6= (x-2)(x²+2x+3)

En fin, sólo lo digo porque le he dado muchas vueltas a esto y para mí esta es la opción más sencilla. Mi problema es que no sé factorizar polinomios con varias incognitas. Del tipo x³+2xy-y²… por poner un ejemplo. No sé si se puede aplicar el teorema del resto o ruffini o si existe otro método. No sé cómo hacerlo cuando aparece el término Bxy.
Muchas gracias, me haríais un gran favor si me contestaseis porque por más que busco no encuentro nada más allá del método ensayo y error y se me va la vida con ese método.

Responder
1. Polinomios
  28/06/2021 a las 20:33
  
  Muy buenas Confusa,
  
  En polinomios con dos o más variables en general no se pueden aplicar las mismas reglas, ya que el hecho de tener más de una variable hace todo más difícil.
  
  Efectivamente, este método de factorización de polinomios que comentas puede resultar muy útil a veces, pero hemos preferido explicar el método general ya que, como dices, se puede usar en más ocasiones. ¡Muchas gracias por tu aportación! ¡Seguro que le puede ayudar a más de un lector! 🙂
  
  En respecto a la factorización de polinomios con dos o más variables, no existe un método específico que sirva para todos los polinomios. Pero normalmente se pueden factorizar extrayendo factor común, ya sea de las incógnitas o de los coeficientes. Puedes ver cómo se hace en nuestro post del factor común.
  
  ¡Muchas gracias también por tu comentario tan trabajado! <3
TIBERI
20/07/2021 a las 23:47

Excelente, aunque faltaron algunos casos

Responder
1. Polinomios
  29/07/2021 a las 13:42
  
  Hola de nuevo Tiberi,
  
  Gracias por tu comentario. ¡Te animo a que compartas con todos los casos que mencionas! 🙂
Cris
09/09/2021 a las 17:41

Excelente!! Muy didácticas las explicaciones Muchas gracias

Responder
1. Polinomios
  12/09/2021 a las 12:30
  
  ¡Muchas gracias Cris! ¡Intentaremos seguir así! 😉
France
29/03/2023 a las 15:19

Hola muchas gracias 💙🖤💜

Responder
1. Polinomios
  11/04/2023 a las 22:05
  
  ¡Gracias a ti por comentar!
2. Irene
  23/05/2023 a las 20:59
  
  Gracias por compartir tu tiempo y conocimientos.

¿Qué es la factorización de polinomios?

Cómo factorizar polinomios con la regla de Ruffini

Factorizar polinomios sin término independiente

Factorizar polinomios con raíces racionales

Casos especiales de la factorización de polinomios

Factorización de identidades notables

Diferencia de cuadrados

Cuadrado de la suma y de la resta

Factorización de trinomios de segundo grado

Factorización de trinomios de cuarto grado con exponentes pares

Factorización de polinomios por agrupación

Ejercicios resueltos de factorización de polinomios

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Ejercicio 6

11 comentarios en “Cómo factorizar polinomios (factorización de polinomios)”

Deja un comentario Cancelar respuesta