Multiplicación algebraica de monomios

Aquí encontrarás qué es y cómo se hace la multiplicación de monomios. Además, podrás ver ejemplos de multiplicaciones de monomios e incluso practicar con ejercicios resueltos paso a paso. Y, finalmente, explicamos las propiedades del producto de monomios.

Cómo multiplicar monomios

Evidentemente, para poder entender cómo se resuelve una multiplicación de monomios primero debes saber qué son los monomios. Así que te recomendamos que le eches un vistazo a la explicación de los monomios antes de seguir.

Entonces, la multiplicación de monomios se hace de la siguiente manera:

En matemáticas, el resultado de la multiplicación de dos monomios es otro monomio cuyo coeficiente es el producto de los coeficientes de los monomios y cuya parte literal se obtiene de multiplicar las variables que tienen la misma base, es decir, sumando sus exponentes.

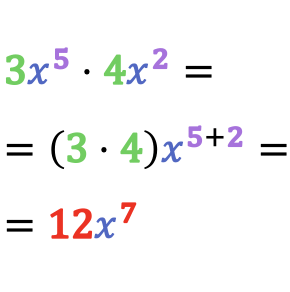
mulitplicacion de monomios con exponentes

Por lo tanto, para multiplicar dos monomios diferentes se deben multiplicar los coeficientes entre sí y sumar los exponentes de las potencias que tengan la misma base.

Sin embargo, si multiplicamos dos monomios con alguna potencia de base distinta, simplemente tenemos que multiplicar sus coeficientes entre sí y dejar las potencias igual. Por ejemplo:

5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4

Por último, debes recordar que, evidentemente, en el producto de los coeficientes de los monomios también se aplica la regla (o ley) de los signos, ya que la multiplicación consiste en una operación aritmética. Por lo tanto:

  • Un monomio positivo por otro monomio positivo es igual a un monomio positivo:

2x^6\cdot 4x^3 = 8x^9

  • Un monomio positivo por un monomio negativo (o viceversa) es equivalente a un monomio negativo:

-2x^6\cdot 4x^3 = -8x^9

2x^6\cdot (-4x^3) = -8x^9

  • Dos monomios negativos multiplicados entre sí da como resultado un monomio positivo:

-2x^6\cdot (-4x^3) = 8x^9

Por otro lado, cabe destacar que el procedimiento de la división de monomios se hace de una manera distinta, de hecho es bastante más complicado. Por eso te recomendamos que visites esta página enlazada donde te explicamos cómo se dividen dos o más monomios y, además, podrás ver ejemplos y practicar con ejercicios resueltos paso a paso.

Ejemplos de multiplicaciones de monomios

Para que puedas entender del todo cómo se multiplican los monomios, a continuación te dejamos con varios ejemplos de la multiplicación entre monomios:

  • 6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9
  • 4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4
  • 5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6
  • -3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z
  • -3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}

Ejercicios resueltos de la multiplicación de monomios

A continuación tienes varios ejercicios resueltos paso a paso de multiplicaciones de monomios para que puedas practicar más:

Ejercicio 1

Calcula las siguientes multiplicaciones de monomios:

\text{A)} \ 3x^4\cdot x^5

\text{B)} \ 2y^8\cdot (-5y^6)

\text{C)} \ 5x^7\cdot 6x^2

\text{D)} \ -4a^3 \cdot (-2a)

\text{A)} \ 3x^4\cdot x^5 = (3\cdot 1)x^{4+5} = \bm{3x^9}

\text{B)} \ 2y^8\cdot (-5y^6)= (2\cdot (-5))y^{8+6} = \bm{-10y^{14}}

\text{C)} \ 5x^7\cdot 6x^2=(5\cdot 6)x^{7+2} = \bm{30x^9}

\text{D)} \ -4a^3 \cdot (-2a) =(-4\cdot (-2))a^{3+1} = \bm{8a^4}

 

Ejercicio 2

Resuelve las siguientes multiplicaciones de monomios:

\text{A)} \ 2x^3\cdot 4x \cdot (-3x^6)

\text{B)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)

\text{C)} \ 3b^2 \cdot (-3b^2) \cdot 6 b^4

\text{D)} \ 7x^3 \cdot 3x^2 \cdot 2x^7

\text{A)} \ 2x^3\cdot 4x \cdot (-3x^6) = 8x^4\cdot (-3x^6) = \bm{-24x^{10}}

\text{B)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)=5x^9\cdot (-9x^4) =\bm{-45x^{13}}

\text{C)} \ 3b^2 \cdot (-3b^2) \cdot 6 b^4=-9b^4\cdot 6 b^4 =\bm{ -54b^8}

\text{D)} \ 7x^3 \cdot 3x^2 \cdot 2x^7 = 21x^5\cdot 2x^7 = \bm{42x^{12}}

 

Ejercicio 3

Simplifica al máximo las siguientes multiplicaciones de monomios:

\text{A)} \ 8x^3y^2 \cdot 5x^4y^7

\text{B)} \ -6x^5y^2z \cdot (-4x^4y^9z^2)

\text{C)} \ -4a^3b^8 \cdot 5 a^3c^2

\text{D)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)

\text{A)} \ 8x^3y^2 \cdot 5x^4y^7 = \bm{40x^7y^9}

\text{B)} \ -6x^5y^2z \cdot (-4x^4y^9z^2) = \bm{24x^9y^{11}z^3}

\text{C)} \ -4a^3b^8 \cdot 5 a^3c^2 = \bm{-20a^6b^8c^2}

\text{D)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)=  35x^{11}y^2z^4\cdot (-2x^2y^5z^3) =  \bm{-70x^{13}y^7z^7}

 

Propiedades de la multiplicación de monomios

El producto de monomios tiene la siguientes propiedades:

  • Propiedad conmutativa: el orden de los monomios multiplicandos no altera el resultado de la multiplicación.

3x^5 \cdot 2x^4 = 6x^9

2x^4 \cdot 3x^5 = 6x^9

  • Propiedad asociativa: cuando se multiplican tres o más monomios, el resultado del producto es el mismo independientemente de como se agrupen los factores:

(2x \cdot 4x^2) \cdot 3x^5 = 24x^8

2x \cdot (4x^2 \cdot 3x^5) = 24x^8

  • Propiedad distributiva: la suma de dos monomios multiplicada por un tercero es igual a la suma de cada sumando por el tercer monomio.

4x^6 \cdot (3x^4+5x^4) = 4x^6 \cdot 3x^4 + 4x^6 \cdot 5x^4

10 comentarios en “Multiplicación algebraica de monomios”

    1. Polinomios

      ¡Muchas gracias Beto! ¡Siempre intentamos hacerlo lo mejor posible! 🙂

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio