En esta página explicamos cómo aplicar la regla de Ruffini para dividir polinomios. Junto con la explicación, podrás ver ejemplos y ejercicios resueltos paso a paso de divisiones de polinomios con la regla de Ruffini. Además, encontrarás todas las aplicaciones de este método y, de hecho, seguro que más de una te sorprende.
Índice
¿Qué es la regla de Ruffini?
En matemáticas, la regla de Ruffini es un método algebraico que permite dividir cualquier polinomio entre polinomios de la forma x-r de manera rápida. La regla de Ruffini recibe este nombre por el matemático Paolo Ruffini, que fue quien inventó este método.
Sin embargo, la regla de Ruffini no solo se usa para dividir polinomios, sino que tiene muchas más utilidades. Por ejemplo, la regla de Ruffini también se utiliza para hallar las raíces de un polinomio, para encontrar el valor numérico de un polinomio, para factorizar un polinomio o incluso para resolver ecuaciones de tercer grado o superior. Más abajo profundizaremos en cómo se aplica la regla de Ruffini para poder hacer todas estas operaciones.
Por último, la regla de Ruffini también se conoce como método de Ruffini, teorema de Ruffini o división sintética de polinomios.
Cómo hacer la regla de Ruffini
Como hemos visto, el principal uso de la regla de Ruffini es dividir un polinomio entre un binomio, es decir, hacer una división del siguiente tipo:
Fíjate que para poder usar la regla de Ruffini el polinomio divisor siempre debe estar formado por una x (con coeficiente igual a 1) y un número (positivo o negativo), de lo contrario no se puede emplear el algoritmo de Ruffini.
Para aplicar la regla de Rufini se debe de seguir todo un procedimiento, así que continuación vamos a resolver un ejemplo paso a paso para ver cómo se hace la regla de Ruffini (o método de Ruffini).
Ejemplo de la Regla de Ruffini
- Resuelve la siguiente división de polinomios usando la regla de Ruffini:
Primero de todo debemos dibujar dos líneas perpendiculares cortándose, y luego colocar el dividendo y el divisor de la siguiente forma:
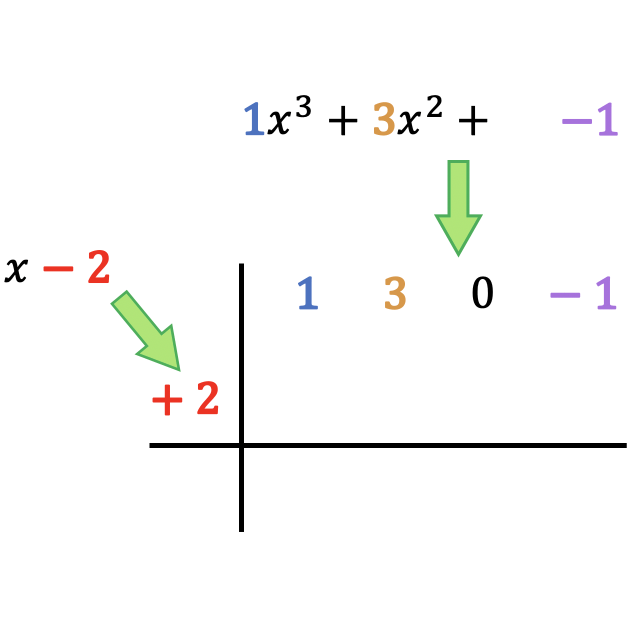
Como puedes ver, debemos poner los coeficientes del polinomio dividendo en la parte de arriba ordenados de mayor a menor grado, y el término independiente del polinomio divisor lo situamos en la izquierda de la caja cambiado de signo.
Atención: Si el polinomio dividendo no tiene un término de un determinado grado (polinomio incompleto), se pone un 0 en su lugar. Por ejemplo, en este caso el polinomio 
no tiene monomio de grado 1, por eso hemos puesto un 0 en su lugar.
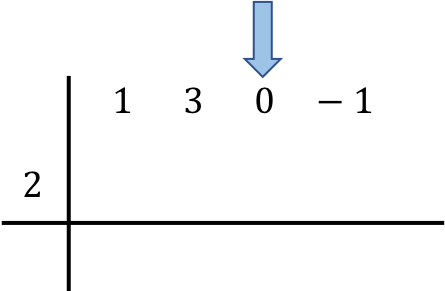
Una vez hemos posicionado los polinomios que intervienen en la operación, bajamos el primer número directamente a la fila de abajo:
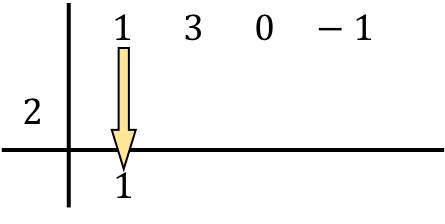
Ahora viene el paso que caracteriza la regla de Ruffini: multiplicamos el número de abajo por el número de la izquierda y colocamos el resultado en la siguiente columna:
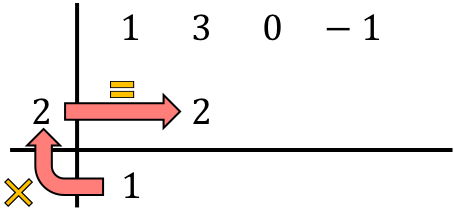
Y sumamos los números de la columna, poniendo el resultado de la suma justo debajo:
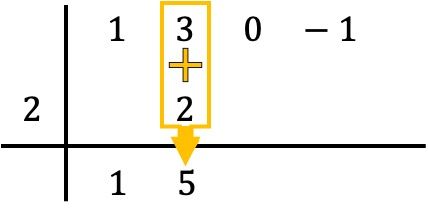
Así pues, el método de Ruffini consiste en ir repitiendo este proceso. Por lo tanto, volvemos a hacer lo mismo: multiplicamos el número de abajo por el número de la izquierda, ponemos el resultado en la siguiente columna y, finalmente, hacemos la suma de los números que están alineados verticalmente:
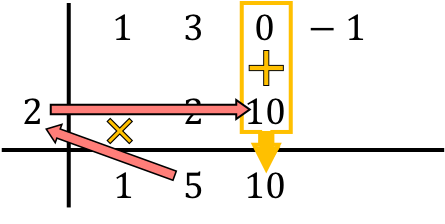
Y vamos repitiendo el mismo procedimiento sucesivamente hasta el final. Primero hacemos el producto del número de abajo por el número de la izquierda, luego colocamos el resultado en la siguiente columna y, por último, sumamos los números de la misma columna:
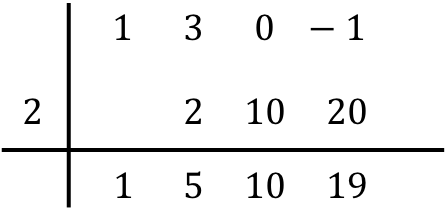
De modo que cuando hemos completado todas las columnas significa que ya hemos terminado la división de polinomios.
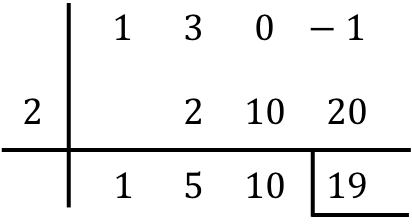
Así que solo nos falta hallar el resultado de la división de los polinomios:
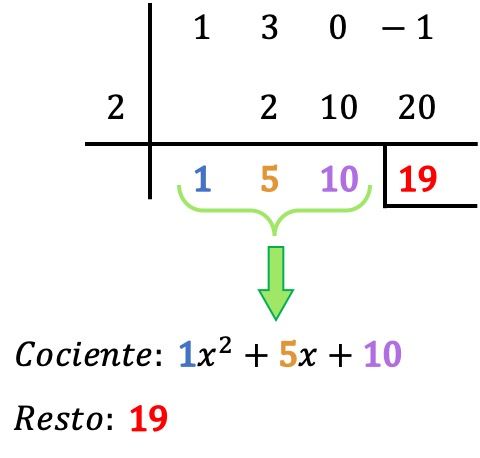
- El resto de la división entre los dos polinomios es el último número de la fila de abajo, por lo que en nuestro caso el residuo es igual a 19. Se suele indicar el resto poniendo una barra a la izquierda y otra debajo de dicho número.
- El cociente de la división polinomial lo determinan los otros valores obtenidos, que son los coeficientes del polinomio del cociente. El primer número empezando por la derecha corresponde al coeficiente del término grado 0, el siguiente número se trata del coeficiente del término de grado 1, el siguiente del grado 2, el siguiente del grado 3,… y así hasta el final. Por lo tanto:
Ejercicios resueltos de la regla de Ruffini
A continuación dispones de varios ejercicios resueltos paso a paso sobre la regla de Ruffini para que puedas practicar y acabes de entender cómo resolver divisiones de polinomios con este método. Te recomendamos que intentes hacer cada ejercicio y luego compruebes si lo has hecho bien mirando la corrección.
Ejercicio 1
Realiza la siguiente división de polinomios con la regla de Ruffini:
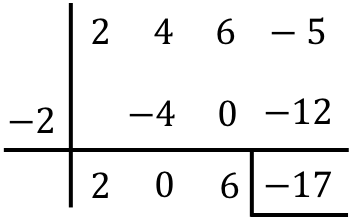
Por tanto el resultado de la división entre los dos polinomios es:
Cociente: 
Resto: 
Ejercicio 2
Calcula la siguiente división de polinomios mediante la regla de Ruffini:
En este caso particular el polinomio dividendo no tiene término de segundo grado, con lo que debemos poner un cero en su lugar:
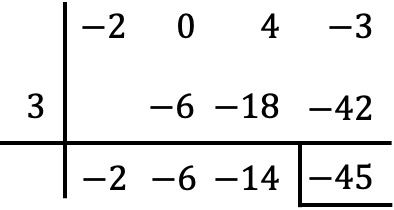
De forma que el resultado de la división entre los 2 polinomios es:
Cociente: 
Resto: 
Ejercicio 3
Halla el resultado de la siguiente división de polinomios por la regla de Ruffini:
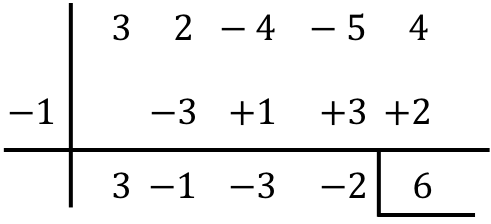
En conclusión, el resultado de dividir a los dos polinomios es:
Cociente: 
Resto: 
Ejercicio 4
Encuentra el valor de la incógnita m para que el resto de la siguiente división de polinomios sea equivalente a 5:
Como el divisor es de la forma (x-r) o (x+r) podemos aplicar la regla de Ruffini para resolver la división. Así que aplicamos el método de Ruffini arrastrando la incógnita m:
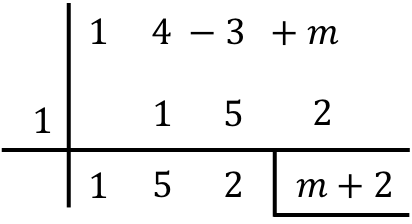
Ahora igualamos el residuo obtenido a 5, porque el resto tiene que ser 5:
Y resolvemos la ecuación para hallar el valor del parámetro m:
Por lo tanto, cuando la variable m sea equivalente a 3 el resto de la división entre los polinomios será igual a 5.
Ejercicio 5
Determina el valor del parámetro m para que el resto de la siguiente división polinómica dé 3:
Como el divisor es de la forma (x-r) o (x+r) podemos aplicar la regla de Ruffini para resolver la división. Por lo tanto, empleamos el método de Ruffini arrastrando la incógnita m:
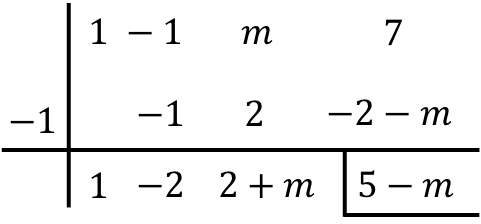
Ten en cuenta la propiedad distributiva al hacer la última multiplicación:
Por otro lado, el cálculo del resto de la división es:
Ahora igualamos la expresión del resto conseguida a 3, ya que el residuo de la división tiene que ser igual a 3:
Y resolvemos la ecuación resultante para determinar el valor del parámetro m:
Por lo tanto, m debe de ser 2 para que el resto de la división polinomial dé 3.
Más aplicaciones de la regla de Ruffini
Como se ha explicado, la regla de Ruffini se usa principalmente para hacer una división entre polinomios. Sin embargo, la regla de Ruffini también sirve para hacer otros cálculos, a continuación vamos a ver todos y cada uno de ellos.
Raíces de un polinomio
Se pueden determinar fácilmente las raíces de un polinomio mediante la regla de Ruffini. Por si no sabes qué es la raíz de un polinomio, vamos a repasar su definición:
Las raíces (o ceros) de un polinomio son los valores que anulan el polinomio. O dicho con otras palabras, las raíces de un polinomio son todos aquellos valores que al evaluarlos en el polinomio su valor numérico es igual a 0.
Por otra parte, sabemos por el teorema del resto que si el valor numérico de un polinomio para un determinado valor 
es nulo, necesariamente el resto de la división de dicho polinomio entre 
también debe de ser 0.
Por lo tanto, si al utilizar la Regla de Ruffini para dividir un polinomio 
entre otro polinomio de la forma obtenemos un resto igual a 0, significa que es una raíz del polinomio 
Seguro que con un ejemplo se entiende mejor:
- Comprueba si
es una raíz del polinomio 
Para comprobar si el valor dado se trata de una raíz del polinomio, simplemente tenemos que aplicar el método de Ruffini con dicho polinomio y dicho valor:
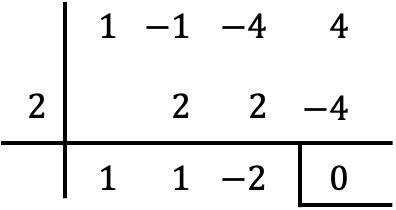
Como el resto obtenido de la regla de Ruffini es igual a cero, quiere decir que efectivamente es una raíz del polinomio
Factorización de polinomios
La regla de Ruffini es el método que se suele aplicar para factorizar polinomios, ya que permite saber de manera rápida todas las raíces de un polinomio de grado 3, 4, 5, etc.
Así pues, veamos cómo se factoriza un polinomio con el algoritmo de Ruffini mediante un ejemplo:
- Factoriza el siguiente polinomio de tercer grado:
Lo primero que debemos hacer es hallar todas las raíces del polinomio. Y las posibles raíces de un polinomio son los divisores del término independiente, que en este caso 6. Por tanto:
Posibles raíces del polinomio: +1, -1, +2, -2, +3, -3, +6, -6
Ahora tenemos que ir probando de dividir el polinomio entre cada uno de estos valores con la regla de Ruffini. Si el resto de la división es igual a 0 significa que el valor es una raíz del polinomio, en cambio, si el resto de la división es distinto de 0 el valor no es una raíz del polinomio. De modo que al probar la regla de Ruffini con todos los números solo se anula el resto en los siguientes tres casos:
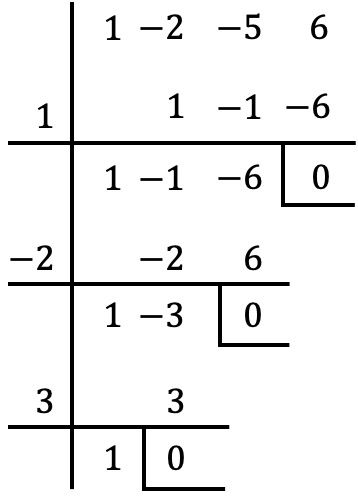
Por lo tanto, las raíces del polinomio del problema son aquellos valores con los que se anula el resto, esto es:
Finalmente, para factorizar el polinomio debemos expresar cada raíz 
en forma de factor del tipo , es decir, por cada raíz debemos poner un paréntesis con una 
y la raíz hallada cambiada de signo:
Como puedes ver, hemos conseguido descomponer el polinomio en factores usando la regla de Ruffini. Sin embargo, es posible que te hayan surgido dudas de la factorización de polinomios, ya que es un tema muy complejo. En tal caso, puedes buscar en nuestra web (en el buscador de arriba a la derecha) el artículo que tenemos sobre cómo factorizar polinomios, allí lo explicamos más detalladamente y podrás practicar con ejercicios resueltos paso a paso. Además, también te mostramos otros métodos para factorizar polinomios.
Calcular el valor numérico de un polinomio
Aunque parezca sorprendente, se puede determinar el valor numérico de un polinomio a través de la regla de Ruffini gracias al teorema del resto.
Pero, evidentemente, para poderlo hacer debes saber qué es el teorema del resto. Si no es el caso, puedes buscar la explicación del teorema del resto en nuestra web (en el buscador de arriba a la derecha).
Así pues, gracias al teorema del resto podemos averiguar el valor numérico de cualquier polinomio. Veamos cómo se hace mediante un ejemplo:
- Calcula el valor numérico de para aplicando la regla de Ruffini, siendo
Para hallar el valor numérico del polinomio para el valor 
lo único que debemos hacer es usar la regla de Ruffini con el polinomio y dicho valor:
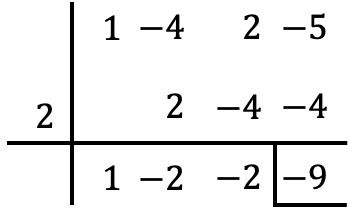
De manera que, a partir del teorema del resto, sabemos que el valor numérico del polinomio coincide con el resto de la división polinómica. Por lo tanto, el valor numérico del polinomio en es -9.
Por otro lado, podemos comprobar que la regla de Ruffini está bien aplicada calculando el valor numérico numéricamente:
![\begin{aligned} P(2) &= 2^3-4\cdot 2^2+2\cdot 2-5\\[2ex] &= 8-4\cdot 4+2\cdot 2-5 \\[2ex] & = 8-16+4-5 \\[2ex] & =\bm{-9} \end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-3a12cf58f19d7b45a6b3c65a5ae68a9c_l3.svg "Rendered by QuickLaTeX.com")
Resolver ecuaciones de tercer grado o superior
Otra aplicación de la regla de Ruffini es resolver ecuaciones de grado superior a 2, ya que en estos casos no existe una fórmula como en la ecuación de segundo grado. Veamos pues cómo se hace mediante un ejemplo:
- Resuelve la siguiente ecuación de tercer grado utilizando la regla de Ruffini:
Debemos tratar la ecuación como si fuese un polinomio. Entonces, tenemos que calcular tantas raíces del «polinomio» por la regla de Ruffini hasta obtener una ecuación de segundo grado. En este caso es una ecuación de grado 3, por lo que solo es necesario determinar una raíz del «polinomio»:
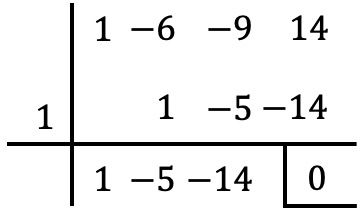
De manera que una solución de la ecuación será 
Pues para hallar las otras soluciones, debemos igualar a 0 el polinomio obtenido en el cociente de la regla de Ruffini:
Y ahora resolvemos la ecuación de segundo grado resultante con su correspondiente fórmula:
![\displaystyle x = \cfrac{5 \pm 9}{2} = \begin{cases} \cfrac{5+9}{2} = \cfrac{14}{2} = 7 \\[4ex]\cfrac{5-9}{2} = \cfrac{-4}{2} = -2 \end{cases}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-b5aeebae94a996c9930d16af37ebfe2e_l3.svg "Rendered by QuickLaTeX.com")
En conclusión, las 3 soluciones de la ecuación de tercer grado son:
Gracias por la información compartida y los ejercicios resueltos. Muy bien especificada y útil, sobre todo en estos tiempos donde no se reciben clases explicativas.
¡Muchas gracias por tu comentario Yelanny! ¡Siempre intentamos hacerlo lo mejor posible!
Muy interesante y didactico
¡Me alegro de que te guste Juan!
Bien explicado.
¡Gracias Susa!
Muchísimas gracias 😌 después de toda una vida creyendo que era mala para las matemáticas está página llegó y lo cambio todo.
buen día ! tengo una duda: la regla de Ruffini está incluida en el teorema de Gauss? o cuál es la relación entre estas dos propiedades? no termino de entender lo que me dejaron mis profesores . . . desde ya, muchas gracias. me viene sirviendo mucho su página !!
Hola Pampi, no la regla de Ruffini no tiene ninguna relación con el método de Gauss, son dos métodos matemáticos distintos. La regla de Ruffini sirve para hallar la raíz de un polinomio o para hacer divisiones, mientras que el método de Gauss permite resolver sistemas de ecuaciones.
Hola,
Excelente y clara explicación de la regla de ruffini para dividir polinomios, factorizar y hallar las raíces del polinomio. No recuerdo haber visto esta regla en mi paso por la universidad.
Mil gracias,
Jorge.
¡Muchísimas gracias Jorger!
MUCHAS GRACIA CREIA QUE SABIA BIEN LA REGLA DE RUFINI, PERO ESTOS EJERCICIOS ME HAN HECHO APRENDER MAS SOBRE ESTE TEMA DE FRACCIONES ALGEBRAICAS CON POLINOMIOS.
¡Genial Mauro! Me alegro de que te haya sido útil.