En esta página se explica qué es y cómo se hace la suma de monomios (semejantes o no). Además, podrás ver ejemplos y practicar con ejercicios resueltos paso a paso de la suma de monomios. Finalmente, también hallarás la explicación de todas las propiedades de la suma de monomios.
Índice
¿Cómo se suman los monomios?
Dos o más monomios solo se pueden sumar si son monomios semejantes, es decir, si ambos monomios tienen una parte literal idéntica (mismas letras y mismos exponentes).
Entonces, la suma de dos monomios semejantes es igual a otro monomio compuesto por la misma parte literal y la suma de los coeficientes de esos dos monomios.
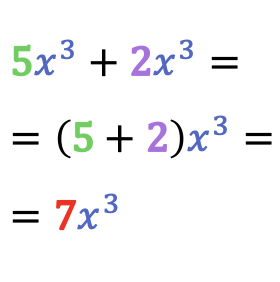
Por lo tanto, al sumar un monomio más otro monomio siempre obtendremos como resultado un monomio semejante a los dos monomios que han intervenido en la suma.
Ejemplos de sumas de monomios
Para que puedas entender del todo cómo sumar dos o más monomios, a continuación puedes ver varios ejemplos:
En definitiva, solamente se pueden sumar los monomios que son semejantes. Y, en tal caso, solo se suman los coeficientes pero la parte literal queda igual.
Ahora que ya has visto cómo se resuelve una suma de monomios, seguramente te interese saber cómo calcular todas las otras operaciones con monomios (resta, multiplicación, división, potencia,…). Por eso te dejamos este enlace donde no solo se explica cómo se hacen todas las operaciones con monomios, sino que, además, se enseña a resolver operaciones combinadas con monomios.
Suma de monomios no semejantes
Acabamos de ver que solamente se pueden sumar monomios semejantes. Por tanto, si nos encontramos con una suma de monomios no semejantes, es decir con el exponente diferente o con alguna variable (letra) distinta, no podemos realizar la suma de dichos monomios de ninguna manera. Y, en ese caso, debemos dejar la operación indicada (sin resolver).
Fíjate en el siguiente ejemplo de suma entre monomios semejantes y no semejantes:
En la expresión algebraica anterior, el monomio tiene una parte literal diferente a los otros, por lo que no lo podemos sumar con los otros términos. En cambio, los otros dos monomios sí que se pueden sumar entre sí:
En conclusión, cuando sumamos dos (o más) monomios no semejantes no los podemos agrupar y, en consecuencia, obtenemos un polinomio.
En cambio, esto es distinto cuando multiplicamos monomios, porque se pueden multiplicar tanto monomios semejantes como monomios no semejantes. Es por eso que te recomendamos que le eches un vistazo a esta página en la que se explica cómo hacer una multiplicación de monomios y cuáles son las diferencias entre la multiplicación y la suma de monomios.
Ejercicios resueltos de la suma de monomios
Para que puedas practicar, a continuación tienes varios ejercicios resueltos paso a paso sobre la suma de monomios:
Ejercicio 1
Realiza las siguientes sumas de monomios:
No se puede realizar la última operación de monomios porque no son semejantes (tienen distinta parte literal).
Ejercicio 2
Resuelve las siguientes sumas de monomios:
Ejercicio 3
Simplifica al máximo las siguientes sumas de monomios:
Para hacer bien este ejercicio debemos recordar que únicamente se pueden sumar si los monomios son semejantes entre sí, por contra, cuando los monomios no son semejantes no se pueden sumar. Por lo tanto:
Propiedades de la suma de monomios
La suma de monomios tiene las siguientes características:
- Propiedad asociativa: cuando se suman 3 o más monomios semejantes siempre se cumple la siguiente igualdad:
- Propiedad conmutativa: sean monomios semejantes o no, el orden de los sumandos no altera el resultado de la suma.
- Elemento neutro: evidentemente, sumar un monomio más cualquier otro monomio de valor numérico cero es equivalente al propio monomio.
- Elemento opuesto: el resultado de sumar cualquier monomio más su monomio opuesto siempre es nulo.

24m³
Hola Allysson, para poder hacer una suma de monomios se necesitan como mínimo 2 monomios.
Si nos escribes la suma de monomios completa la resolveremos.
-35x⁶y³
y²
Hola Allysson de nuevo, estos dos monomios no se pueden sumar porque no son semejantes (no tienen la misma parte literal).
Quiero saber de ejercicio de-324 su parte literal
Hola Celso, -324 no es un monomio, porque no tiene ninguna variable. Por lo tanto, no tiene parte literal.
Cuál es la respuesta de -2x,3y
Hola Ross,
Estos dos monomios no son semejantes, por lo que no se pueden sumar.
Cual seria la suma de – 5az^2 2az^2 – 3az^2.
En este caso los tres monomios son semejantes, así que para sumarlos simplemente debemos sumar sus coeficientes:

«El resultado» de la suma de monomios no semejantes puede ser acomodada de diferente orden ?
Ejemplo:
4x⁷+2x³+ 5×3= 4x⁷ + 7x³
ó 7x³+4x⁷
Son válidos la forma de los dos resultados?
Hola Mau,
Sí, son válidas ambas formas, ya que el orden de una suma no altera el resultado. Aunque lo más común es poner primero los términos de mayor grado, el resultado de una suma de monomios no depende del orden en el que se ponen.
Me podria podrian ayudar con esta suma de Monomios 25 a3 b2 c + 15 cb2 a 3 – 7
Claro Karina, te dejo resuelta la suma de monomios a continuación:
Fíjate que no puedes sumar el término sin incógnita con los otros dos monomios porque no tienen la misma parte literal, en cambio, los otros dos monomios se pueden sumar porque son semejantes.
Cómo puedo sumar 3/2rs+8rs
8/3mn+4/6mn+6mn
7/6×2+-5×2+-7/6×2
Hola Liceth,
Todas las sumas (o restas) de monomios que has propuesto están formadas por monomios semejantes, por lo que simplemente tienes que sumar los coeficientes de los monomios:
Cual seria la suma de (-abcd) + (-abcd)
Hola Arlet,
Los dos monomios son exactamente iguales, por lo tanto, la suma de ambos queda de la siguiente manera;:
