Identidades notables (o productos notables)

Aquí encontrarás la explicación de cómo resolver todos los tipos de identidades notables (o productos notables). Podrás ver cuáles son las fórmulas de todas las identidades notables, junto con ejemplos y ejercicios resueltos paso a paso. Además, te mostraremos para qué sirven estas reglas matemáticas tan famosas.

👉👉 A continuación te explicamos paso a paso cada identidad notable, pero si lo prefieres puedes ir directamente a la 😉 tabla donde están resumidas todas las fórmulas. 👈👈

¿Qué son las identidades notables (o productos notables)?

Las identidades notables, también conocidas como productos notables o igualdades notables, son reglas matemáticas que permiten resolver de manera directa operaciones con polinomios.

Las fórmulas de las identidades notables más comunes son el cuadrado de una suma, el cuadrado de una diferencia (o resta), y la suma por la diferencia.

identidades productos o igualdades notables

Pero a continuación no solo te enseñaremos cómo calcular estos productos notables, sino que te mostraremos todos los tipos de identidades notables que existen.

Fórmulas de las identidades (o productos) notables

Una vez hemos visto la definición de los productos notables (o igualdades notables), vamos a ver cuáles son las fórmulas de las identidades notables. Por otro lado, si tienes interés en las demostraciones de las fórmulas, puedes hacer que se muestren haciendo click en los botones de «ver demostración de la fórmula».

Cuadrado de una suma

El cuadrado de una suma, o suma al cuadrado, es una de las principales identidades notables. En concreto, se trata de un binomio con dos términos positivos elevado a la 2, es decir, su expresión algebraica es (a+b)2.

Así pues, la fórmula del cuadrado de una suma es:

identidades notables cuadrado de una suma

Si empezamos con un binomio positivo elevado a la 2:

(a+b)^2

Matemáticamente, el cuadrado anterior es equivalente al factor (a+b) multiplicado por sí mismo:

(a+b)^2=(a+b)\cdot (a+b)

Entonces, hacemos la multiplicación de polinomios utilizando la propiedad distributiva:

\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}

De los cuatro términos obtenidos, ab y ba son semejantes así que los podemos agrupar:

a^2+ab+ba+b^2 = a^2+2ab+b^2

De modo que ya hemos llegado a la expresión de la fórmula de una suma al cuadrado, por lo que queda demostrada:

(a+b)^2= a^2+2ab+b^2

Como curiosidad, el desarrollo de la expresión de este tipo de producto notable se llama trinomio cuadrado perfecto.

De modo que el cuadrado de una suma es igual al cuadrado del primer término, más el doble del producto del primero por el segundo, más el cuadrado del segundo.

Así que para resolver una suma al cuadrado no basta con elevar cada sumando a la dos, sino que, además, se debe multiplicar los dos sumandos entre sí y por 2. Es importante recordar esto ya que un error muy típico de este tipo de producto notable es olvidarse de este término.

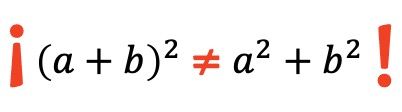
identidades notables polinomio y binomio

Ejemplo:

  • Calcula la siguiente identidad notable aplicando su fórmula correspondiente:

(x+5)^2

Tal y como acabamos de ver, la fórmula de la igualdad notable de una suma al cuadrado es:

(a+b)^2=a^2+2ab+b^2

Por lo tanto, primero tenemos que identificar los parámetros a y b de la fórmula. En este caso, a representa la x del binomio y b corresponde al número 5:

\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}

Entonces, ahora que ya sabemos los valores de a y de b, podemos utilizar la fórmula de un binomio positivo al cuadrado para hallar el resultado:

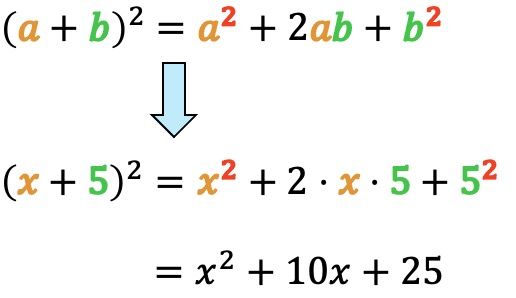
ejemplos de identidades notables al cuadrado
 

Cuadrado de una diferencia

El cuadrado de una diferencia, o diferencia al cuadrado, es otra de las 3 identidades notables más utilizadas. En particular, corresponde a un binomio formado por un término positivo y otro término negativo elevado a la 2, esto es, su expresión algebraica es (a-b)2.

Entonces, la fórmula del cuadrado de una diferencia (o cuadrado de una resta) es la siguiente:

productos notables al cuadrado

Partiendo de la expresión del binomio de una resta elevado al cuadrado:

(a-b)^2

Evidentemente, la potencia anterior es igual al producto del factor (a-b) multiplicado por sí mismo:

(a-b)^2= (a-b)\cdot (a-b)

Ahora multiplicamos los dos paréntesis aplicando la propiedad distributiva:

\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}

De manera que solo nos queda agrupar los términos semejantes para acabar de verificar la fórmula:

a^2-ab-ba+b^2 = a^2-2ab +b^2

Entonces, la fórmula del cuadrado de una diferencia queda matemáticamente demostrada:

(a-b)^2=a^2-2ab+b^2

De forma que el cuadrado de una diferencia es igual al cuadrado del primer término, menos el doble del producto del primero por el segundo, más el cuadrado del segundo.

Al igual que con la igualdad notable de la suma al cuadrado, no debemos olvidar de poner el término intermedio de la fórmula, ya que la siguiente ecuación es incorrecta:

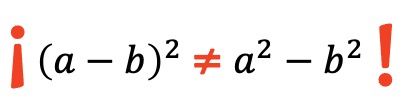
errores comunes de las identidades notables

Ejemplo:

  • Resuelve la siguiente igualdad notable de una diferencia elevada al cuadrado:

(x-3)^2

Se trata del producto notable de una resta al cuadrado, por lo tanto, tenemos que aplicar su fórmula correspondiente:

(a-b)^2=a^2-2ab+b^2

Luego, tenemos que identificar cuáles son los valores de las incógnitas a y b de la fórmula. En este caso, a es la variable x y b corresponde al número 3:

\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}

Fíjate que el signo negativo no forma parte del parámetro b, sino que siempre debemos coger el número sin el signo para aplicar correctamente esta fórmula.

De modo que ya sabemos los valores de a y de b, por tanto, solo tenemos que sustituir dichos valores en la fórmula para solucionar la identidad notable:

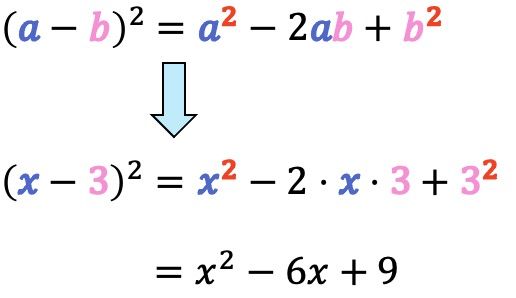
ejemplos y ejercicios resueltos paso a paso de igualdades notables
 

Suma por diferencia

El producto de una suma por una diferencia es una de las 3 identidades notables más usadas. Tal y como indica su nombre, se trata de un binomio positivo multiplicado por su binomio conjugado (mismo binomio pero con el signo intermedio cambiado), es decir, la expresión algebraica de este tipo de producto notable es (a+b)·(a-b).

La fórmula de la identidad notable del producto de una suma por una diferencia es la siguiente:

identidades, productos e igualdades notables de secundaria 2, 3, y 4 eso

Empezando desde el producto de una suma por una resta de dos términos cualesquiera:

(a+b)\cdot (a-b)

Para demostrar la fórmula simplemente tenemos que multiplicar el primer paréntesis por el segundo paréntesis mediante la propiedad distributiva:

\begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}

Ahora agrupamos los términos semejantes:

a^2 -ab+ba-b^2=a^2-b^2

Y de esta forma hemos llegado a la expresión de la igualdad notable. Por lo que la fórmula de este tipo de identidad notable queda demostrada:

(a+b)\cdot (a-b) =a^2-b^2

Entonces, el producto de la suma por la diferencia de dos cantidades es igual a la diferencia de los cuadrados de esas cantidades. O dicho con otras palabras, multiplicar la suma de dos términos distintos por la resta de esos dos mismos términos es equivalente a elevar al cuadrado cada uno de los 2 términos y restarlos.

Ejemplo:

  • Halla, usando la fórmula correspondiente, el siguiente producto notable de la suma por la diferencia de dos términos distintos:

(x+2)\cdot (x-2)

Como hemos visto arriba, la fórmula de la igualdad notable de una suma por una diferencia es la siguiente:

(a+b)\cdot (a-b) =a^2-b^2

En primer lugar, lo que debemos hacer es identificar los valores de las letras a y b de la fórmula. En este caso a corresponde a la variable x y b corresponde al número 2.

\left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}

Y cuando ya conocemos qué valores toman los parámetros a y b, aplicamos la fórmula del producto de la suma por la diferencia:

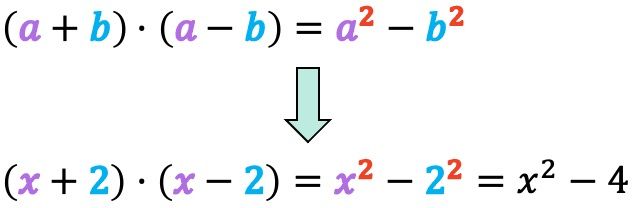
ejemplos y ejercicios resueltos paso a paso de productos notables
 

Cuadrado de un trinomio

El cuadrado de un trinomio (polinomio formado por 3 términos) es igual al cuadrado del primer término, más el cuadrado del segundo término, más el cuadrado del tercer término, más el doble del primero por el segundo, más el doble del primero por el tercero, más el doble del segundo por el tercero.

cuales son las formulas de todas las identidades, productos o igualdades notables

Empezando con un trinomio cualquiera elevado al cuadrado:

(a+b+c)^2

El cuadrado anterior se puede descomponer factorialmente en el trinomio multiplicado por sí mismo:

(a+b+c)^2 = (a+b+c)(a+b+c)

Ahora resolvemos la multiplicación polinómica:

(a+b+c)(a+b+c)= a^2+ab+ac+ba+b^2+bc+ca+cb+c^2

Y, por último, agrupamos los términos semejantes:

a^2+ab+ac+ba+b^2+bc+ca+cb+c^2 = a^2+b^2+c^2+2ab+2ac+2bc

De esta manera ya hemos llegado a la expresión de la fórmula, así que se demuestra la fórmula del cuadrado de un trinomio:

(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc

Ejemplo:

  • Halla la siguiente igualdad notable:

\left(x^2+x+3\right)^2

La fórmula del cuadrado de un trinomio es:

(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc

Como en todas las igualdades notables, primero debemos identificar los valores de las incógnitas de la fórmula. En este ejercicio a es x^2, el coeficiente b corresponde a la x, y c es el término independiente 3:

\left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}

Y cuando ya sabemos los valores, únicamente tenemos que sustituir dichos valores en la fórmula y hacer los cálculos:

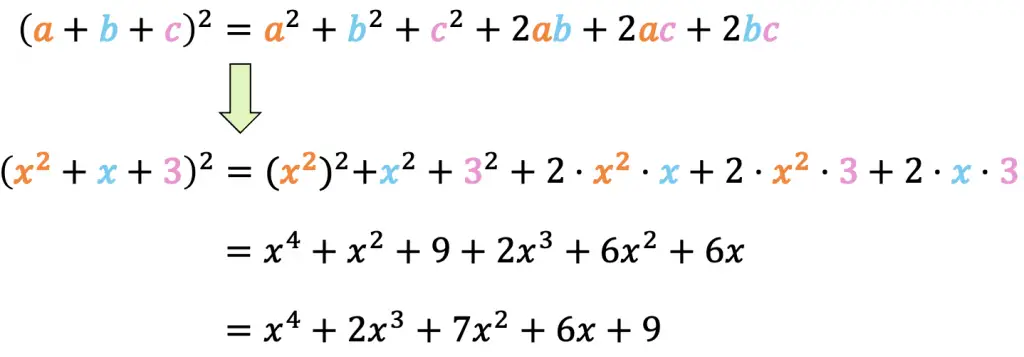
calculadora de identidades, productos e igualdades notables

 

Identidades (o productos) notables al cubo

Acabamos de estudiar todas las identidades notables al cuadrado, es decir, todos los tipos de identidades notables que están formadas por potencias elevadas a la 2. Pues ahora vamos a analizar las identidades notables al cubo. Lógicamente, las fórmulas de las identidades al cubo son un poco más complicadas, pero también resultan muy útiles.

Cubo de una suma

El producto notable del cubo de una suma es un binomio (polinomio con solo dos monomios) elevado a la 3 cuyos dos elementos son positivos. Por lo tanto, algebraicamente el cubo de un suma se expresa como (a+b)3.

La fórmula de la igualdad notable del cubo de una suma es:

cuales son todos los productos, identidades o igualdades notables

Partiendo de un binomio positivo elevado al cubo:

(a+b)^3

La potencia anterior se puede descomponer factorialmente en el producto del factor (a+b) por su cuadrado:

(a+b)^3=(a+b)\cdot (a+b)^2

Asimismo, como hemos visto en las igualdades notables al cuadrado, el binomio (a+b) se puede resolver con la fórmula del cuadrado de una suma:

(a+b)\cdot (a+b)^2=(a+b)\cdot (a^2+2ab+b^2)

Luego multiplicamos los dos polinomios entre sí:

\begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}

Para terminar, solamente nos queda agrupar los términos semejantes:

a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 = a^3+3a^2b+3ab^2+b^3

Y de este modo queda comprobada la fórmula de la identidad notable de un binomio suma elevado al cubo:

(a+b)^3 = a^3+3a^2b+3ab^2 +b^3

En definitiva, una suma elevada a la 3 es igual al cubo del primero, más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo.

Ejemplo:

  • Resuelve la siguiente identidad notable de una suma al cubo utilizando su fórmula correspondiente:

(x+2)^3

En este problema tenemos un binomio elevado a la 3 cuyos dos términos son positivos. Por tanto, tenemos que emplear la fórmula de una suma elevada al cubo:

(a+b)^3 = a^3+3a^2b+3ab^2 +b^3

Ahora debemos averiguar el valor de los parámetros a y b de la fórmula. En este caso, a corresponde a la variable x y b es el número 2.

\left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}

Con lo que calculamos el producto notable sustituyendo los valores de a y de b en la fórmula:

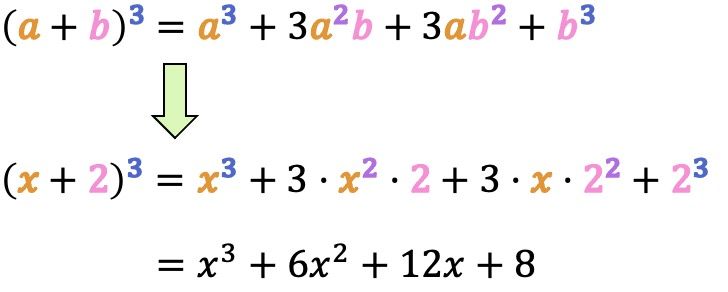
10 ejemplos de productos o identidades notables
 

Cubo de una diferencia

El cubo de una diferencia, o cubo de una resta, es un binomio elevado a la 3 que tiene un término con signo negativo. Así pues, la expresión matemática de este tipo de producto notable es (a-b)3.

La fórmula del cubo de una diferencia (o resta) es:

identidades, productos o igualdades notables cubicas

Obviamente, la demostración de esta fórmula es muy parecida a la del producto notable de una suma al cubo. Pero en este caso partimos de un binomio negativo al cubo:

(a-b)^3

Evidentemente, la potenciación anterior se puede descomponer en el producto del factor (a-b) multiplicado por su cuadrado:

(a-b)^3=(a-b)\cdot (a-b)^2

Luego, como hemos estudiado en las identidades notables al cuadrado, el binomio (a-b) se puede calcular con la fórmula del cuadrado de una diferencia:

(a-b)\cdot (a-b)^2=(a-b)\cdot (a^2-2ab+b^2)

Ahora hacemos el producto de los dos polinomios:

\begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}

Y el último paso es agrupar los términos semejantes:

a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 = a^3-3a^2b+3ab^2-b^3

Así que queda comprobada la fórmula de la identidad notable de un binomio resta elevado al cubo:

(a-b)^3 = a^3-3a^2b+3ab^2-b^3

Por lo tanto, una diferencia (o una resta) elevada a la tres es equivalente al cubo del primero, menos el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, menos el cubo del segundo.

Ejemplo:

  • Calcula el siguiente binomio al cubo (diferencia) utilizando su fórmula correspondiente:

(3x-2)^3

En este ejercicio tenemos un binomio con un elemento positivo y otro negativo. Por lo que debemos usar la fórmula de una diferencia elevada al cubo:

(a-b)^3 = a^3-3a^2b+3ab^2 -b^3

En primer lugar, como siempre, identificamos el valor de las incógnitas a y b de la fórmula. En este caso a representa el monomio 3x y b es el término independiente del binomio, esto es, 2.

\left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}

Fíjate que el parámetro b equivale simplemente a 2, sin el signo negativo del número. Es importante tener esto en cuenta para aplicar bien la fórmula.

Por último, hallamos la identidad notable poniendo los valores de a y de b en la fórmula:

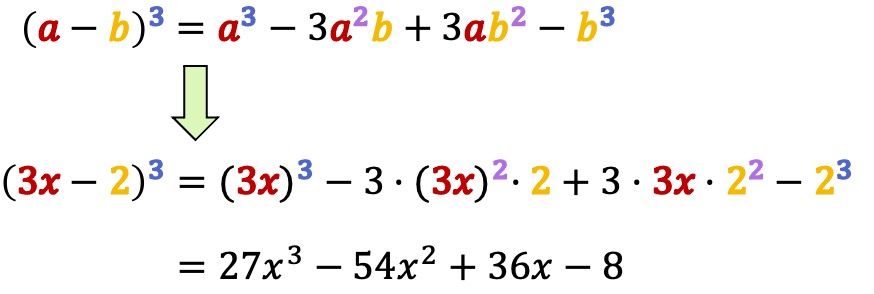
desarrollar identidades, productos e igualdades notables

 

Tabla resumen de las identidades notables

A modo de resumen, hemos hecho una tabla con todas las identidades (o productos) notables que hemos visto, así te será más fácil estudiarlas. 😉

formulas de las identidades productos o igualdades notables

 

Ejercicios resueltos de identidades (o productos) notables

Para que acabes de entender el concepto de identidades notables, también llamadas productos notables o igualdades notables, te hemos preparado varios ejercicios resueltos paso a paso. Puedes intentar hacerlos y luego comprobar si lo has hecho bien con las soluciones de los ejercicios.

⬇⬇ ¡Recuerda que puedes preguntarnos cualquier duda que tengas abajo en los comentarios! ⬇⬇

Ejercicio 1

Desarrolla las siguientes identidades notables (sumas al cuadrado):

\text{A)} \ (x+3)^2

\text{B)} \ (6x+2)^2

\text{C)} \ \left(x^2+7\right)^2

\text{D)} \ (5x+8y)^2

Todas las identidades notables del problema son sumas al cuadrado, por lo que en este caso siempre tenemos que aplicar la misma fórmula:

(a+b)^2=a^2+2ab+b^2

 

\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}

 

\text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}

 

\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}

 

\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}

 

Ejercicio 2

Desarrolla los siguientes productos notables (diferencias al cuadrado):

\text{A)} \ (x-2)^2

\text{B)} \ (3-7x)^2

\text{C)} \ \left(x^2-6\right)^2

\text{D)} \ (-3x+y)^2

Todas los productos notables de este ejercicio son restas elevadas al cuadrado, así que solamente debemos aplicar una única fórmula:

(a-b)^2=a^2-2ab+b^2

 

\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}

 

\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}

 

\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}

 

\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}

 

Ejercicio 3

Desarrolla las siguientes igualdades notables (productos de sumas por diferencias):

\text{A)} \ (x+5)(x-5)

\text{B)} \ (2x+6)(2x-6)

\text{C)} \ (x+7)(x-7)

\text{D)} \ (x-4y)(x+4y)

Como todas las igualdades notables de este ejercicio son multiplicaciones de sumas por diferencias, todas ellas se solucionan con la misma fórmula:

(a+b)\cdot (a-b) =a^2-b^2

 

\text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}

 

\text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}

 

\text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}

 

\text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}

 

Ejercicio 4

Resuelve todas las siguientes identidades notables:

\text{A)} \ \left(x^2+10\right)\left(x^2-10\right)

\text{B)} \ \left(4x^2+2y^3\right)^2

\text{C)} \ \left(6x^3-4y^4\right)^2

\text{D)} \ \left(8x^3+y^2\right)\left(8x^3-y^2\right)

\text{E)} \ \left(5x^2-9x\right)^2

\text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}

 

\text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}

 

\text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}

 

\text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}

 

\text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}

 

Ejercicio 5

Calcula los siguientes productos notables:

\text{A)} \ (x+4)^3

\text{B)} \ \left(x^2-5\right)^3

\text{C)} \ \left(2x-1\right)^3

\text{D)} \ (5x+2)^3

Para hallar todos los productos notables del problema debemos aplicar las fórmulas de una suma y de una diferencia al cubo dependiendo del caso:

(a+b)^3 = a^3+3a^2b+3ab^2 +b^3

(a-b)^3 = a^3-3a^2b+3ab^2-b^3

 

\text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}

 

\text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}

 

\text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}

 

\text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}

 

Ejercicio 6

Resuelve las siguientes igualdades notables:

\text{A)} \ \left(x^2+x+5\right)^2

\text{B)} \ \left(x^2+3x-4\right)^2

\text{C)} \ \left(4x^2-6x+3\right)^2

\text{D)} \ \left(x^3-3x^2-9x\right)^2

Para resolver todas estas identidades notables debemos emplear la fórmula del cuadrado de un trinomio, que es:

(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc

 

\text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}

 

\text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}

 

\text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}

 

\text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}

 

Ejercicio 7

Calcula las siguientes identidades notables con raíces y fracciones (dificultad alta):

\text{A)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2

\text{B)} \ \displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right)

\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2

\text{D)} \ \Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr)

El apartado A) consiste en una resta elevada al cuadrado, así que para solucionarla se debe aplicar su fórmula correspondiente y, además, hay que recordar que si se eleva una raíz al cuadrado esta queda simplificada:

\text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}

 

El apartado B) se trata de una suma por una resta y los monomios tienen coeficientes fraccionarios, con lo que debemos determinar este producto notable mediante la fórmula de una suma por una resta y las propiedades de las fracciones:

\text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}

 

La igualdad notable del apartado C) es una suma elevada a la 2 y, asimismo, está formada por fracciones. Por tanto, para calcularla tenemos que usar la fórmula de una suma al cuadrado más las propiedades de las fracciones:

\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}

 

La última identidad notable se trata de una suma por una diferencia con coeficientes irracionales, por lo tanto, aplicamos la fórmula de una suma por una diferencia y luego simplificamos las raíces elevadas al cuadrado:

\text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}

 

Otros tipos de identidades notables

Todas las identidades notables que hemos analizado arriba son las que se utilizan más comúnmente. Sin embargo, en matemáticas hay otros tipos de productos notables que también resultan interesantes saberlos, ya que se usan para diferentes fines.

Suma de cubos

La suma de cubos corresponde a un binomio cuyos dos términos son positivos y, además, sus raíces cúbicas son exactas. Por lo tanto, la expresión algebraica de una suma de cubos es a3+b3.

identidades, productos o igualdades notables resueltas

La fórmula de este producto notable sirve para factorizar un polinomio, es decir, a través de la fórmula transformamos un polinomio en un producto de un binomio por un trinomio.

Para que puedas ver cómo se hace, a continuación tienes un ejemplo de cómo aplicar esta identidad notable:

x^3+8

Efectivamente, la expresión anterior consiste en una adición de cubos porque la raíz cúbica del monomio x^3 es exacta (no da un número decimal) y la del número 8 también:

\sqrt[3]{x^3} = x

\sqrt[3]{8} = 2

x^3+8=x^3+2^3

Por tanto, podemos emplear la fórmula de la suma de cubos perfectos para transformar la expresión cúbica en un producto de un binomio por un trinomio:

a^3+b^3 = (a+b)(a^2-ab+b^2)

\begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}

Diferencia de cubos

La diferencia (o resta) de cubos es un binomio compuesto por un término positivo y un término negativo cuyas raíces cúbicas son exactas. O dicho de otra manera, una diferencia de cubos se expresa de la forma a3-b3.

ejercicios resueltos de factorizar polinomios con identidades notables

Vamos a hacer un ejemplo para que puedas ver cómo se resuelve este tipo de identidad notable:

x^3-27

Se trata de una diferencia de cubos porque tanto la raíz cúbica del monomio x^3 como la de 27 son exactas:

\sqrt[3]{x^3} = x

\sqrt[3]{27} = 3

x^3-27=x^3-3^3

Así que se puede usar la fórmula de la diferencia de cubos perfectos para factorizar el binomio:

a^3-b^3 = (a-b)(a^2+ab+b^2)

\begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}

Producto de binomios con un término común

Este producto notable sirve para convertir un producto de dos binomios que tienen un término en común en un polinomio de segundo grado.

identidades, productos o igualdades notables pdf

Seguidamente tienes un ejemplo resuelto de este tipo de producto notable:

\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}

Más identidades

Aunque las identidades notables son las más famosas porque son las más habituales, cabe destacar que también existen más identidades con otros nombres. A continuación te dejamos con una lista de otras identidades menos conocidas por si tienes curiosidad:

  • Identidades de Lagrange:
    • (a^2+b^2)\cdot (x^2+y^2) =(ax+by)^2+(ay-bx)^2
    • (a^2-b^2)\cdot (x^2-y^2) =(ax+by)^2-(ay+bx)^2
  • Identidades de Legendre:
    • (a+b)^2+(a-b)^2=2(a^2+b^2)
    • (a+b)^2-(a-b)^2=4ab
    • (a+b)^4-(a-b)^4=8ab(a^2+b^2)
  • Identidad de Argand:
    • (x^2+x+1)(x^2-x+1) = x^4+x^2+1
  • Identidades de Gauss:
    • a^3+b^3+c^3-3abc= (a+b+c)(a^2+b^2+c^2-ab-bc-ac)
    • a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]

Aplicaciones de las identidades notables

Si has llegado hasta aquí significa que ya sabes cómo hacer cálculos con las identidades notables. ¡Genial! Pero realmente… ¿para qué sirven las identidades notables? ¿Y cuándo se usan las identidades notables?

Tal y como hemos visto a lo largo de este artículo, la principal utilidad de las identidades notables es simplificar cálculos. Es decir, gracias a los productos notables podemos resolver directamente algunas potencias de polinomios complejas sin necesidad de hacer operaciones difíciles.

Pero las igualdades notables también tienen otras funciones, como por ejemplo factorizar polinomios y completar cuadrados. A continuación vamos a ver en qué consiste cada una de estas aplicaciones.

Factorización de polinomios

Algunos tipos de polinomios muy concretos se pueden llegar a factorizar con las identidades notables. Por ejemplo, si nos encontramos con un polinomio formado por dos términos que son cuadrados perfectos (sus raíces cuadradas son exactas), este se puede factorizar mediante la fórmula de la igualdad notable del producto de una suma por una diferencia:

a^2-b^2 =(a+b)(a-b)

x^2-9 =(x+3)(x-3)

Igualmente, se pueden factorizar los trinomios que cumplen con las identidades notables del cuadrado de una suma o de una resta:

a^2+2ab+b^2=(a+b)^2

x^2+4x+4=(x+2)^2

a^2-2ab+b^2=(a-b)^2

x^2-10x+25=(x-5)^2

Asimismo, una vez se ha factorizado un polinomio, se pueden averiguar las raíces (o ceros) de dicho polinomio. Aún así, este concepto es un poco más complicado de entender, por lo que si estás más interesad@ te recomendamos que busques la explicación en el buscador de nuestra web (arriba a la derecha), ya que tenemos un artículo entero explicándolo.

Completación de cuadrados

La completación de cuadrados es un procedimiento matemático que se usa para convertir un trinomio de segundo grado en la suma de un cuadrado más (o menos) un número.

Dado un trinomio cualquiera:

ax^2+bx+c

Entonces, se puede transformar el trinomio en la siguiente expresión:

a(x+h)^2+k

Donde los parámetros h y k se calculan con las siguientes fórmulas:

h=\cfrac{b}{2a} \qquad \qquad k=c-ah^2

Aunque seguramente no te lo parezca, estas dos fórmulas se deducen a partir de las identidades notables. Así que gracias a a los productos notables se pueden completar cuadrados.

A modo de ejemplo, vamos a aplicar este procedimiento al siguiente trinomio:

2x^2+4x+3

Calculamos los parámetros h y k:

h=\cfrac{b}{2a}=\cfrac{4}{2\cdot 2} =1

k=c-ah^2 = 3-2\cdot 1^2 = 1

Y, por tanto, el polinomio queda:

2(x+1)^2+1

7 comentarios en “Identidades notables (o productos notables)”

    1. Polinomios

      ¡Muchísimas gracias! Recuerda que puedes ayudarnos compartiendo el artículo. 😉

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio