Resta de polinomios

En esta página explicamos cómo se hace la resta de polinomios. Además, encontrarás varios ejemplos y ejercicios resueltos paso a paso de restas de polinomios.

¿Cómo se hace la resta de polinomios?

Para hacer la resta de dos polinomios se deben restar los términos de los polinomios que son semejantes. Es decir, la resta de polinomios consiste en restar los términos que tienen la misma parte literal (mismas variables y mismos exponentes).

En matemáticas, se puede calcular la resta de polinomios de dos formas diferentes: con el método vertical o con el método horizontal. A continuación tienes la explicación de ambos procedimientos, pero te aconsejamos que primero aprendas cómo restar polinomios de manera vertical y luego pases al método horizontal. Aunque evidentemente quédate con el que tú prefieras.

Resta de polinomios vertical

A continuación vamos a ver cómo se restan dos polinomios de manera vertical mediante un ejemplo:

• Realiza la resta siendo ambos polinomios:

Lo primero que debemos hacer para hallar cualquier resta de polinomios es poner un polinomio debajo del otro, de manera que los términos semejantes de los dos polinomios estén alineados por columnas:

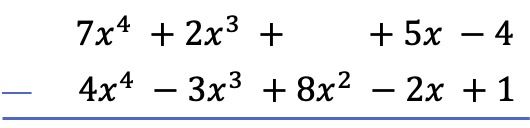
Atención: Si un polinomio no tiene término de un determinado grado, debemos dejar el espacio en blanco. Por ejemplo, el polinomio no tiene monomio de segundo grado, por eso hay un espacio vacío en su sitio.

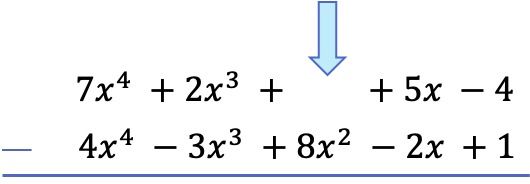
Aunque ahora ya se podrían restar los polinomios directamente, es bastante fácil equivocarse con lo signos si lo hacemos de esta manera. Por lo tanto, para realizar la resta de polinomios es mejor cambiar de signo a todos los términos del polinomio sustraendo (el polinomio que resta) y luego hacer la suma. Ya que restar un polinomio es equivalente a sumar su polinomio opuesto.

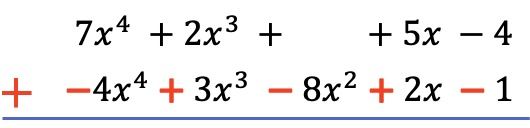
Y una vez hemos ordenado todos los términos por orden de mayor a menor grado y hemos negado los términos del polinomio de abajo, sumamos los coeficientes de cada columna manteniendo las partes literales iguales:

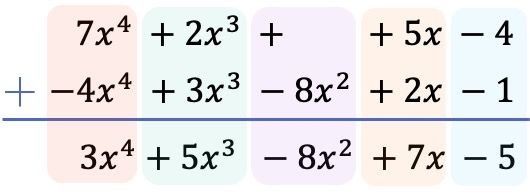
Por lo tanto, el resultado obtenido de la resta de los 2 polinomios es:

Por si no te ha quedado claro el último paso, te dejo con la explicación de cómo se hace la suma de polinomios, de hecho es imprescindible que domines la suma de polinomios para poder restar bien polinomios. En la página enlazada también encontrarás ejemplos y ejercicios resueltos de sumas de polinomios y, además, podrás ver las diferencias entre la suma y la resta de polinomios.

Resta de polinomios horizontal

Acabamos de ver cómo se restan los polinomios verticalmente, pero ahora vamos a ver el otro método que existe para hacer resta de polinomios: restar polinomios horizontalmente. Seguramente este procedimiento es más rápido que el anterior, sin embargo es necesario tener un dominio superior de los conceptos de los polinomios.

Así pues, veamos en qué consiste este método de restar polinomios mediante un ejemplo. Y para que puedas ver las diferencias entre los dos métodos, restaremos los mismos polinomios que en el ejemplo anterior:

• Calcula la resta siendo los dos polinomios:

En primer lugar, tenemos que poner los dos polinomios en forma de operación algebraica, o dicho con otras palabras, uno detrás del otro:

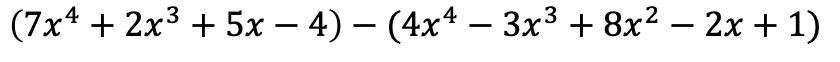
Los monomios del primer paréntesis permanecen igual, por contra, los términos del segundo paréntesis se tienen que cambiar de signo porque tienen un negativo delante:

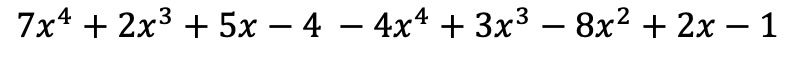
Y ahora agrupamos los términos que tienen partes literales idénticas, es decir, los términos con las mismas variables (letras) y los mismos exponentes. Los términos que no son semejantes no se pueden ni sumar ni restar.

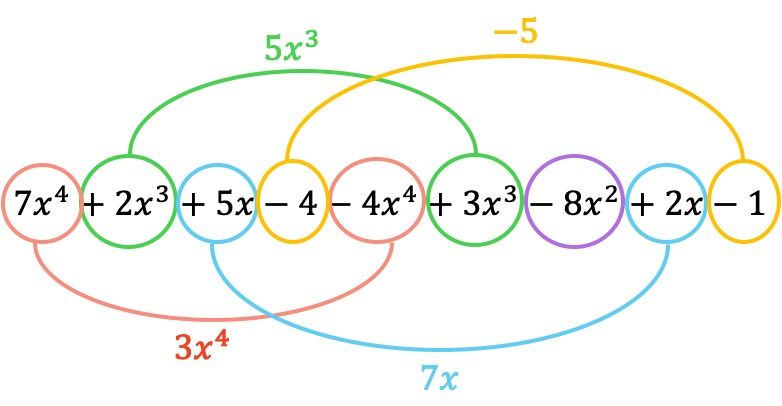
De modo que el polinomio resultante de la resta es:

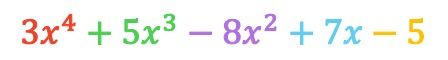
Como puedes comprobar hemos obtenido el mismo resultado con los dos métodos, así que puedes usar el que te vaya mejor.

Ahora que ya has visto los 2 métodos que hay para resolver una resta de polinomios, ¿sabías que también se pueden restar fracciones con polinomios? Y no solo restas, sino todo tipo de operaciones. Descubre cómo se hacen las operaciones con fracciones algebraicas haciendo click en este enlace.

Ejercicios resueltos de la resta de polinomios

Para que puedas practicar, te dejamos con varios ejercicios resueltos de restas de polinomios. Si tienes alguna duda sobre algún ejercicio puedes preguntarla en los comentarios de la página, la contestaremos lo antes posible.

Ejercicio 1

Resta el polinomio menos el polinomio

En este caso, restaremos los dos polinomios de manera vertical. Para ello, primero ordenamos los polinomios por grado, después cambiamos de signo los términos del polinomio que resta y, finalmente, sumamos los monomios situados en la misma columna:

 

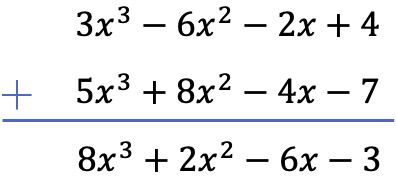
Ejercicio 2

Resuelve la resta el polinomio menos el polinomio

Restar dos polinomios es lo mismo que sumar al polinomio minuendo el opuesto del polinomio sustraendo. Por lo tanto, cambiamos de signo los términos del polinomio sustraendo (el que resta) y sumamos los polinomios:

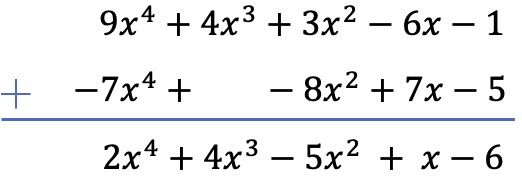
Fíjate que en este caso particular se debe dejar un espacio vacío en la columna de grado 3 del segundo polinomio, ya que no tiene término de tercer grado.

 

Ejercicio 3

Halla el resultado de la resta del polinomio menos el polinomio

En este caso, resolveremos la resta de los dos polinomios de manera vertical. Así que primero ponemos los polinomios por orden de mayor a menor grado, después cambiamos de signo los términos del polinomio que resta y, por último, sumamos los términos semejantes:

 

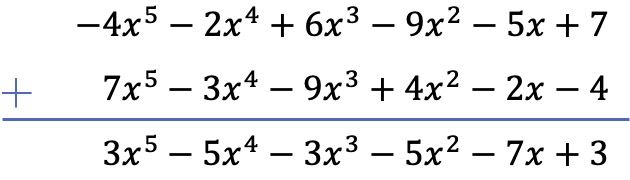
Ejercicio 4

Calcula la siguiente operación con polinomios:

En este caso intervienen 3 polinomios en la operación, de los cuales 2 están restando. Por lo que para resolver la operación cambiaremos de signo a todos los términos de los dos polinomios que restan y luego sumaremos los polinomios.

 

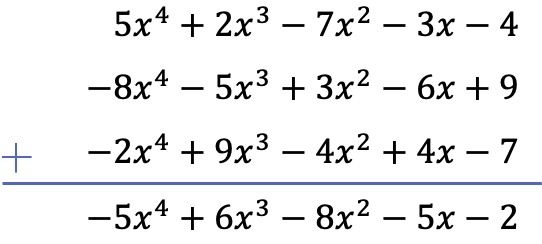
¿Qué te ha parecido la explicación? ¿Te ha resultado útil? ¿Tú con qué método para restar polinomios te quedas, el vertical o el horizontal? ¡Os leemos en los comentarios! 👀