En esta página explicamos qué es el triángulo de Tartaglia, también llamado triángulo de Pascal. Enseñamos cómo construir matemáticamente el triángulo de Tartaglia (o de Pascal), así como para qué sirve y cuáles son todas sus propiedades. Finalmente, mostramos cómo y cuándo se originó este triángulo tan importante.
Índice
¿Qué es el triángulo de Tartaglia (o de Pascal)?
El triángulo de Tartaglia, también conocido como triángulo de Pascal, es una representación matemática de números enteros ordenados en forma de triángulo. El triángulo de Tartaglia (o de Pascal) sirve para hacer cálculos matemáticos.
Esta es la definición del triángulo de Tartaglia o de Pascal, pero seguro que entiendes mejor el concepto con una imagen del triángulo:
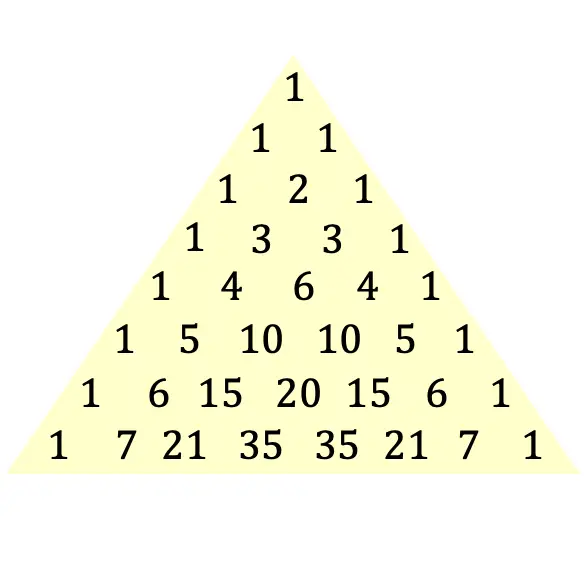
El triángulo de Tartaglia también se llama triángulo de Pascal en honor al filósofo y matemático francés Blaise Pascal, que fue quien introdujo esta expresión triangular en 1654, aunque este triángulo ya se conocía desde la antigüedad. Más abajo profundizaremos en la historia de este triángulo tan peculiar.
¿Cómo se construye el triángulo de Tartaglia o de Pascal?
Como has podido comprobar en el triángulo de Pascal (o Tartaglia) hay muchos números, pero esto no significa que los tengamos que saber de memoria (menos mal). Existe una fórmula que permite hallar todos los números del triángulo de Pascal o Tartaglia fácilmente, tan solo se deben resolver sumas sencillas.
Para construir el triángulo de Tartaglia o de Pascal se empieza con la cúspide del triángulo que siempre es un 1, y luego se van calculando las filas de abajo. Cada número de las filas posteriores corresponde a la suma de los dos números que tiene justo encima, excepto los extremos de las filas que siempre son 1.
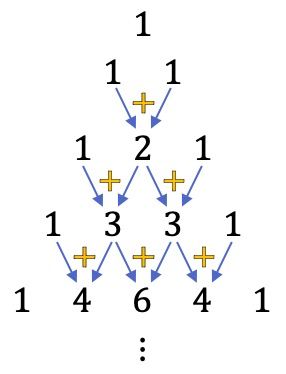
Por lo tanto, se pueden calcular tantas filas del triángulo de Tartaglia como se quiera, porque se pueden ir añadiendo filas sucesivamente sumando los números.
¿Para qué sirve el triángulo de Tartaglia o de Pascal?
Saber hacer la construcción del triángulo de Tartaglia está muy bien, pero… ¿para qué se utiliza este triángulo aritmético? Pues bien, el triángulo de Tartaglia (o de Pascal) tiene muchas aplicaciones en las matemáticas, especialmente en el campo del álgebra.
Números combinatorios
En primer lugar, el triángulo de Tartaglia se usa para calcular directamente números combinatorios, también llamados coeficientes binomiales. Si no sabes qué son este tipo de operaciones, puedes buscarlo en nuestra web (arriba a la derecha tenemos un buscador) ya que escribimos un artículo detallado donde explicamos cómo se resuelven y en él también hallarás ejemplos y ejercicios resueltos paso a paso. Pero a modo de resumen, la expresión algebraica de un número combinatorio es la siguiente:
Pues todos los números combinatorios se pueden determinar de manera fácil con el triángulo de Tartaglia, porque la solución de cada coeficiente binomial equivale a un número de esta expresión triangular tal y como se aprecia en la siguiente figura:
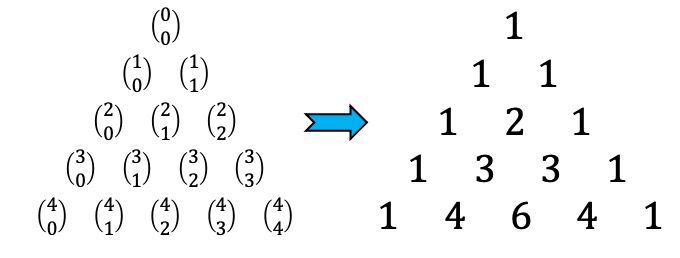
Por ejemplo, el número combinatorio da como resultado 6, porque en el triángulo de Tartaglia hay un 6 en su lugar.
De manera que si sabes cómo construir el triángulo de Tartaglia o Pascal, puedes calcular cualquier número combinatorio rápidamente y sin usar su fórmula.
Binomio de Newton
Otro uso del triángulo de Tartaglia (o de Pascal) es poder calcular potencias de binomios (haz click en este enlace para saber qué es un binomio).
Un ejemplo de la potenciación de un binomio son las identidades notables, como por ejemplo:
Las identidades notables son muy importantes para las matemáticas, ya que permiten ahorrar muchos cálculos y resolver operaciones complicadas de manera directa y rápida. Por eso te recomendamos que le eches un vistazo al siguiente enlace si aún no sabes qué son las identidades notables.
Como has podido ver en el enlace anterior, los productos notables se pueden resolver directamente con sus fórmulas. Pero… ¿qué pasa cuando el binomio está elevado al cubo o a un grado mayor?
Pues bien, estos binomios se pueden calcular de una manera muy sencilla con el triángulo de Tartaglia gracias al teorema del binomio (o binomio de Newton). Aunque una vez dominas el método resulta rápido aplicarlo, para explicarlo bien se necesita una página entera. Por lo que si estás más interesado en cómo resolver este tipo de binomios haz click en la página enlazada y podrás ver cómo se hace.
Combinatoria
El triángulo de Tartaglia, o triángulo de Pascal, también se puede emplear para determinar combinaciones y probabilidades.
Si alguna vez nos encontramos con un problema en el que debemos averiguar cuántas agrupaciones diferentes se pueden hacer de un grupo sin que importe el orden, podemos utilizar el triángulo de Tartaglia.
Por ejemplo, si tenemos 5 cartas, para saber de cuántas maneras podemos elegir 3 de ellas basta con ir a la tercera columna (la primera columna es la cero) de la quinta fila (la primera fila también es la fila 0) del triángulo de Tartaglia. El número en esa posición (10) corresponde al número de posibilidades que hay para escoger 3 cartas.
Por lo tanto, a partir de 5 cartas se pueden formar 10 grupos diferentes de tres cartas.
Propiedades del triángulo de Tartaglia o de Pascal
El triángulo de Tartaglia, también llamado triángulo de Pascal, tiene las siguientes carcterísticas:
- El triángulo de Tartaglia (o de Pascal) es simétrico, es decir, la línea vertical que divide todo el triángulo en dos triángulos equiláteros iguales es un eje de simetría.
- La suma horizontal de todos los números de cualquier fila del triángulo de Pascal es equivalente a una potencia de 2.
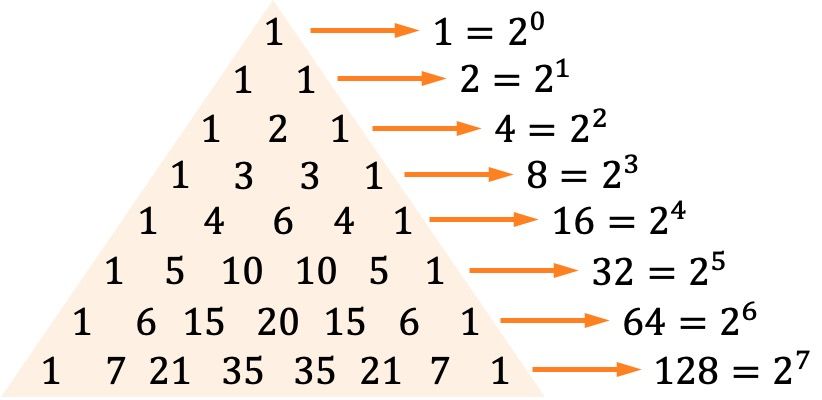
- Las diagonales del triángulo de Tartaglia también son importantes: los números de la primera diagonal (diagonal externa) son unos, la segunda diagonal está formada por la sucesión todos los números naturales, la tercera diagonal corresponde a los números triangulares, y la cuarta diagonal está compuesta por los números tetragonales (o tetraédricos).
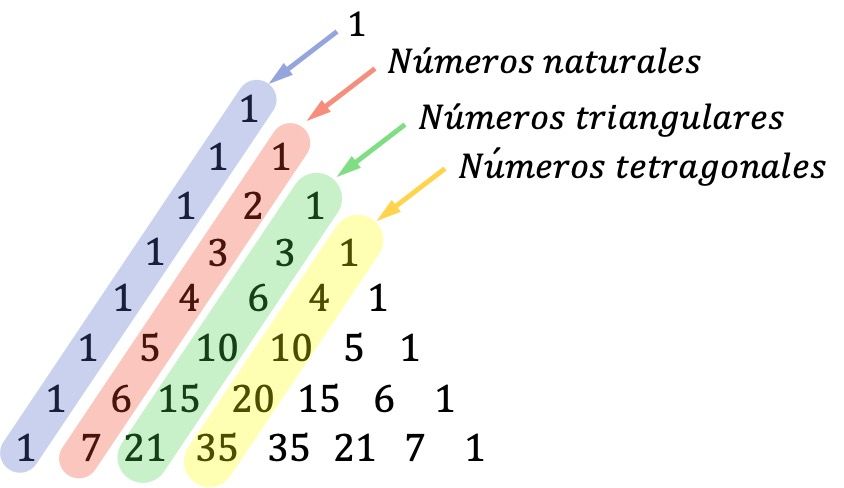
Los números triangulares son números que se pueden representar en forma de triángulo. Y los números tetragonales son aquellos que forman pirámides triangulares.
Si no conoces cuáles son los números triangulares o tetragonales no pasa nada, es simplemente una curiosidad del triángulo de Tartaglia. Sin embargo, sí que deberías saber el significado de números naturales (números que se utilizan para contar elementos).
- Exceptuando el número 1, si el primer número de una fila es un número primo, todos los números que están en esa misma fila son divisibles entre dicho número. Por ejemplo, en la octava fila (1-7-21-35-35-21-7-1) los números 7, 21 y 35 se pueden dividir entre 7 (siete es un número primo).
- Otra peculiaridad del triángulo de Tartaglia es que se puede hallar la serie de Fibonacci sumando las diagonales de una forma determinada:
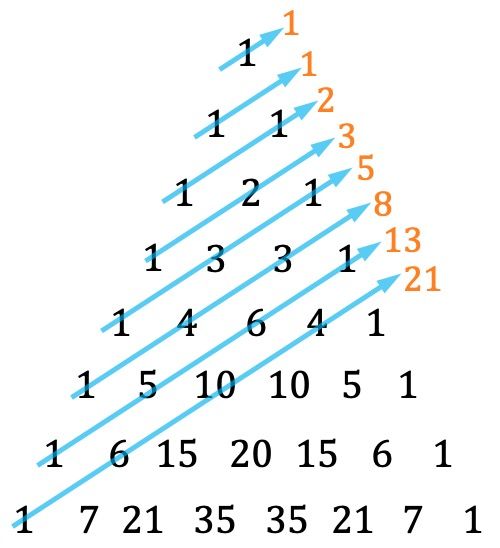
Recuerda que cada término de la sucesión de Fibonacci es igual a la suma de los dos anteriores, siendo los dos primeros términos 1 y 1. De modo que los números que pertenecen a la serie de Fibonacci son: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,…
- Si sumamos dos números consecutivos de la tercera diagonal del triangulo de Pascal (1-3-6-10-15-…) obtenemos como resultado un cuadrado perfecto (1, 4, 9, 16, 25,…).
- Si pintamos los números pares del triángulo de Pascal de un color y los números impares de otro color, se obtiene la figura del triángulo de Sierpinski, un famoso conjunto geométrico. A continuación puedes ver el triángulo de Pascal con una altura de 512 representado con los números impares de color negro y los números pares de color blanco:

- La conjectura de Singmaster dice que el número de veces que aparece cada número superior a 1 es finito. O dicho con otras palabras, aunque el número de filas del triángulo de Tartaglia es infinto, las veces que aparece cada número menos el 1 sí que es finito. Como curiosidad, el número 3003 es el único que se sabe hasta el momento que aparece hasta ocho veces en el triángulo.
Historia del triángulo de Tartaglia o Pascal
Ahora que ya sabemos cómo es el triángulo de Tartaglia, veamos cuándo se inventó este triángulo matemático tan especial.
Aunque el nombre del triángulo aritmético se atribuye principalmente a los célebres científicos Tartaglia y Pascal, este triángulo algebraico ya se utilizaba anteriormente.
El primer registro de un triángulo formado por coeficientes binomiales data del siglo X en Índia. Sin embargo, empezaron a estudiar sus propiedades los persas, en particular los matemáticos Al-Karaji (953-1029) y Omar Khayyam (1048-1131). Por eso en Irán se popularizó como triángulo de Khayyam-Pascal o incluso únicamente triángulo de Khayyam.
En China se empezó a introducir este triángulo en el siglo XI a través del matemático Jia Xian, pero fue más tarde en el siglo XIII cuando Yang Hui lo presentó bajo el nombre de triángulo aritmético. Y por este motivo en el país asiático le dicen triángulo de Yang Hui.
El triángulo matemático llegó al continente europeo más adelante a través del alemán Petrus Apianus, concretamente lo publicó en el año 1527 en su libro Rechnung. A partir de aquí el famoso algebrista italiano Niccolò Fontana Tartaglia estudió profundamente el triángulo durante la primera mitad del siglo XVI, y en honor a él en países como Italia se conoce como triángulo de Tartaglia.
Por último, el francés Blaise Pascal demostró muchas de las propiedades del triángulo estudiado en su publicación del Traité du triangle arithmétique (Tratado del triángulo aritmético) en 1654, de aquí viene el nombre de triángulo de Pascal. Cabe destacar que algunas de estas propiedades ya se sabían, pero fue Pascal quien logró su demostración mediante la inducción matemática.
