▷ Cómo multiplicar polinomios (ejercicios resueltos)

En esta página encontrarás cómo se multiplican los polinomios. También podrás ver ejemplos de multiplicaciones de polinomios y, además, ejercicios resueltos paso a paso. Por último, hallarás cuáles son las propiedades de la multiplicación de polinomios.

Sin embargo, para entender bien el concepto de la multiplicación de polinomios iremos de lo más básico a lo más complicado, es decir, empezaremos por cómo se multiplica un polinomio por un número, luego veremos cómo se hace la multiplicación de un polinomio por un monomio y, finalmente, explicaremos cómo multiplicar dos o más polinomios entre sí.

Yo te aconsejo que sigas este orden, pero si crees que ya dominas las operaciones con polinomios previas puedes ir directamente a la multiplicación entre polinomios haciendo click en el índice:

Índice

Multiplicación de un polinomio por un número

El producto de un escalar (o un número) por un polinomio es bastante fácil de resolver, simplemente se debe multiplicar el número por el coeficiente de cada término del polinomio.

multiplicacion de un numero por un polinomio

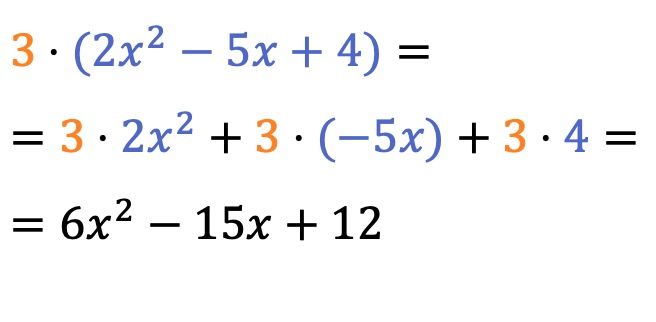
El signo de multiplicación de delante del paréntesis se puede omitir.

$\begin{array}{l} 2\cdot (5x^4-6x^2) = \\[2ex] =2 (5x^4-6x^2)= \\[2ex] = 10x^4-12x^2 \end{array}$

Multiplicación de un polinomio por un monomio

Antes de ver cómo multiplicar un polinomio por un monomio, primero vamos a recordar cómo se multiplican los monomios entre sí, porque es necesario saberlo para poder hacer este tipo de operación polinomial.

El producto de dos monomios consiste en multiplicar sus coeficientes entre sí y sus partes literales entre sí, es decir, se multiplican los coeficientes de los monomios y se suman los exponentes de las variables que tienen la misma base. Fíjate en el siguiente ejemplo:

$3x^2 \cdot 4x^5 = (3\cdot 4) x^{2+5} = 12x^7$

Ahora sí, veamos cómo se realiza la multiplicación de un monomio por un polinomio:

En matemáticas, para resolver la multiplicación un monomio por un polinomio se multiplica el monomio por cada término del polinomio.

multiplicacion de un polinomio por un monomio

Al igual que antes, el signo de multiplicación también puede ser omitido:

$\begin{array}{l} -4x \cdot (2x^3-5x^2)= \\[2ex] =-4x (2x^3-5x^2)=\\[2ex] = -4x\cdot 2x^3 -4x \cdot (-5x^2) = \\[2ex] =-8x^4 +20x^3 \end{array}$

Fíjate en el ejemplo anterior que cuando multiplicamos monomios o polinomios también hay que tener en cuenta la regla de los signos. De hecho, un error muy típico de las multiplicaciones entre monomios y polinomios es equivocarse por el signo de un término.

Seguro que alguna vez cuando has visto algo nuevo en matemáticas te has preguntado: ¿y para qué demonios sirve esto? Pues bien, este tipo de multiplicación se utiliza para sacar factor común de un polinomio, una operación que permite simplificar los polinomios (muy útil). Puedes ver qué es y cómo se calcula el factor común de un polinomio en este enlace.

Multiplicación de dos polinomios

Una vez ya sabemos cómo multiplicar polinomios por números y por monomios, vamos a ver qué es y cómo se hace la multiplicación de polinomios por polinomios.

Para hacer una multiplicación de polinomios se deben seguir los siguientes pasos:

Multiplicar cada término del primer polinomio por todos los términos del segundo polinomio.
Sumar (o restar) los monomios del mismo grado (monomios semejantes).

Para que veas exactamente en qué consiste este método vamos a resolver paso a paso la siguiente multiplicación de polinomios:

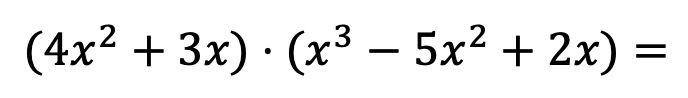
En primer lugar, tenemos que multiplicar cada elemento del primer polinomio multiplicador por cada término del segundo polinomio:

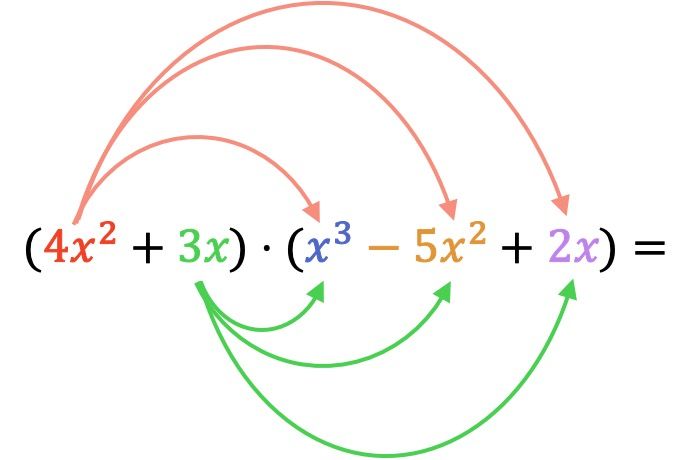
multiplicacion de polinomios paso a paso

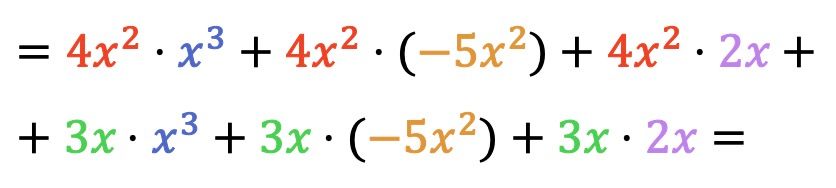
Ahora hacemos todas las multiplicaciones de monomios:

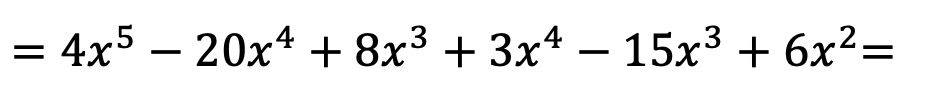
Una vez hemos multiplicado los polinomios entre sí, tan solo tenemos que agrupar los términos resultantes que sean semejantes, o dicho de otra forma, los términos con la misma letra y el mismo exponente:

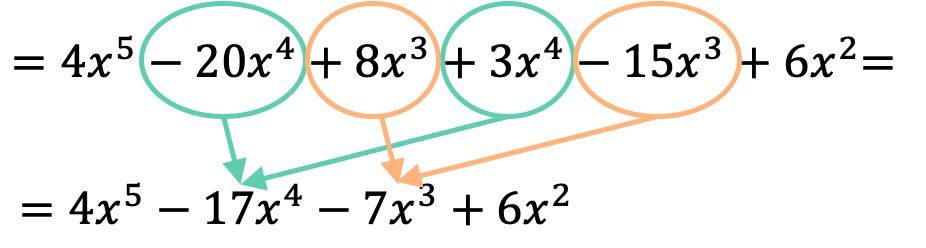
multiplicacion de polinomios por polinomios

De modo que el resultado de la multiplicación polinómica es:

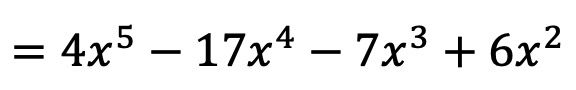
Y de esta forma ya hemos calculado la multiplicación de polinomios. Quizás ahora te parece muy difícil, pero ya verás que cuando practiques con dos o tres ejercicios te resultará mucho más fácil.

Ahora que ya has visto cómo se resuelve la multiplicación entre dos polinomios, seguramente te interese saber cómo hacer una división de polinomios. De hecho, dividir polinomios es mucho más complicado que multiplicarlos, por eso hemos explicado paso a paso el procedimiento (y trucos😉) para que lo puedas entender perfectamente. Si te interesa, haz click en este enlace para ver cómo se dividen los polinomios.

Multiplicación de polinomios vertical

Acabamos de ver cómo se multiplica un polinomio por otro polinomio de manera horizontal, pero también se puede hacer de una forma más clásica: multiplicar polinomios de manera vertical. Veamos pues cómo se utiliza este método resolviendo un ejemplo de una multiplicación polinomial.

Si queremos multiplicar verticalmente los siguientes dos polinomios:

$(5x^2+3x-4) \cdot (2x^2-x)$

Lo primero que debemos hacer es colocar un polinomio debajo del otro, en forma de multiplicación algebraica de polinomios:

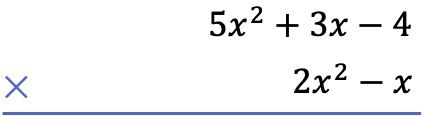
En segundo lugar, multiplicamos cada término del polinomio de abajo por cada término del polinomio de arriba, y ponemos los resultados ordenados por columnas de mayor a menor grado:

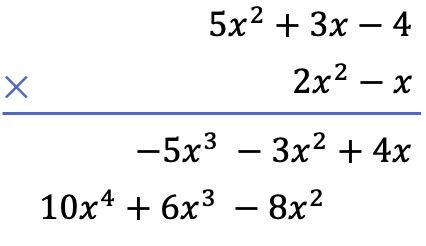
Y, por último, sumamos los términos que están alineados verticalmente:

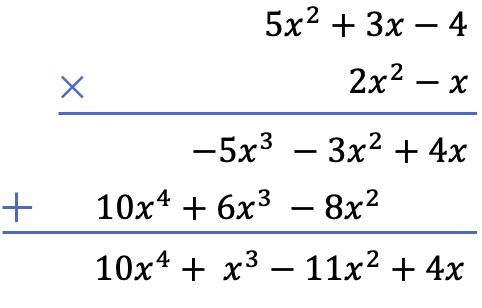
Ahora que ya has visto los 2 métodos que existen para resolver una multiplicación de polinomios, ¿sabías que también se pueden multiplicar fracciones con polinomios? Y no solo multiplicaciones, sino que se pueden hacer todo tipo de operaciones con este tipo de fracciones. Haz click en este enlace y descubre qué son las fracciones algebraicas.

Propiedades de la multiplicación de polinomios

La multiplicación de polinomios cumple con las siguientes características:

Propiedad conmutativa: el orden de los polinomios multiplicandos no altera el resultado de la multiplicación.

$P(x)\cdot Q(x) = Q(x) \cdot P(x)$

Propiedad asociativa: cuando se multiplican tres o más polinomios, el resultado del producto es el mismo independientemente de como se agrupen los factores:

$\bigl(P(x) \cdot Q(x)\bigr) \cdot R(x) =P(x) \cdot \bigl(Q(x) \cdot R(x)\bigr)$

Propiedad distributiva: la suma de dos polinomios multiplicada por un tercero es igual a la suma de cada sumando por el tercer polinomio.

$P(x)\cdot \bigl(Q(x)+ R(x)\bigr) = P(x)\cdot Q(x) + P(x) \cdot R(x)$

El grado del polinomio resultante de una multiplicación entre dos polinomios es igual a la suma de los grados de los dos polinomios que se estaban multiplicando.

Ejercicios resueltos de multiplicaciones de polinomios

Para que puedas practicar, te dejo con varios ejercicios resueltos de la multiplicación de polinomios. Puedes probar de resolverlos tú y comprobar tus resultados con la solución propuesta. Luego puedes preguntarnos cualquier duda que tengas en los comentarios, estaremos encantados de ayudarte.

Ejercicio 1

Calcula los siguientes productos entre polinomios y escalares:

$\text{A)} \ 4\cdot (2x^3-4x)$

$\text{B)} \ -3 \cdot (-5x^2+9x)$

$\text{C)} \ 5\cdot(3x^2+4x-7)$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7)$

Ver solución

Para calcular la multiplicación de un polinomio por un número debemos multiplicar el número por el coeficiente de cada elemento del polinomio. Por lo tanto:

$\text{A)} \ 4\cdot (2x^3-4x) =4 \cdot 2x^3 -4\cdot 4x = \bm{8x^3-16x}$

$\text{B)} \ -3 \cdot (-5x^2+9x) = -3 \cdot (-5x^2)-3\cdot 9x = \bm{15x^2-27x}$

$\text{C)} \ 5\cdot(3x^2+4x-7) = \bm{15x^2+20x-35}$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7) = \bm{-24x^5+36x^3-48x^2+42}$

Ejercicio 2

Resuelve las siguientes multiplicaciones entre polinomios y monomios:

$\text{A)} \ 2x \cdot (5x^2+3)$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5)$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x)$

Ver solución

Para resolver la multiplicación de un polinomio por un monomio debemos multiplicar dicho monomio por cada término del polinomio. Por lo tanto:

$\text{A)} \ 2x \cdot (5x^2+3) = 2x \cdot 5x^2+2x\cdot 3 = \bm{10x^3+6x}$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)= -4x^2 \cdot 6x^4 - 4x^2 \cdot (-9x^2) = \bm{-24x^6+36x^4}$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5) = \bm{10x^6-10x^5+25x^3}$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x) = \bm{21x^8-12x^7-3x^5-9x^3}$

Ejercicio 3

Determina el resultado de las siguientes multiplicaciones entre polinomios:

$\text{A)} \ (4x^2 + 1) \cdot (3x^2-2)$

$\text{B)} \ (-3x^4+2x) \cdot (5x^4-x)$

$\text{C)} \ (2x^3-5x^2)\cdot (4x-7)$

Ver solución

Para calcular una multiplicación de dos polinomios debemos multiplicar cada elemento del primer polinomio por cada elemento del segundo polinomio, y luego agrupar los términos semejantes. Por lo tanto:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2 + 1) \cdot (3x^2-2) = \\[2ex] =4x^2 \cdot 3x^2 +4x^2\cdot (-2) +1 \cdot 3x^2 +1 \cdot (-2) = \\[2ex] = 12x^4-8x^2+3x^2 -2 = \\[2ex] = \bm{12x^4-5x^2-2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (-3x^4+2x) \cdot (5x^4-x) = \\[2ex] =-3x^4\cdot 5x^4 -3x^4\cdot (-x) +2x \cdot 5x^4 +2x \cdot (-x) = \\[2ex] = -15x^8+3x^5+10x^5-2x^2 = \\[2ex] = \bm{-15x^8+13x^5-2x^2} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^3-5x^2)\cdot (4x-7) = \\[2ex] =2x^3\cdot 4x +2x^3\cdot (-7) -5x^2 \cdot 4x -5x^2\cdot (-7) = \\[2ex] = 8x^4-14x^3-20x^3+35x^2 = \\[2ex] = \bm{8x^4-34x^3+35x^2} \end{array}$

Ejercicio 4

Halla el resultado de las siguientes multiplicaciones entre polinomios:

$\text{A)} \ (4x^2-6x+2) \cdot (5x^3-x^2)$

$\text{B)} \ (3x^3-2x+7) \cdot (-4x^3+5x)$

$\text{C)} \ (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3)$

Ver solución

Para calcular una multiplicación de dos polinomios debemos multiplicar cada elemento del primer polinomio por cada elemento del segundo polinomio, y luego sumar los términos semejantes. Por lo tanto:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2-6x+2) \cdot (5x^3-x^2) = \\[2ex] =4x^2 \cdot 5x^3 +4x^2\cdot (-x^2) -6x \cdot 5x^3 -6x \cdot (-x^2) + 2 \cdot 5x^3 +2 \cdot (-x^2) = \\[2ex] = 20x^5-4x^4-30x^4+6x^3+10x^3-2x^2 = \\[2ex] = \bm{20x^5-34x^4+16x^3-2x^2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (3x^3-2x+7) \cdot (-4x^3+5x) = \\[2ex] =3x^3 \cdot (-4x^3) +3x^3\cdot 5x -2x \cdot (-4x^3) -2x \cdot 5x + 7 \cdot (-4x^3) +7 \cdot 5x = \\[2ex] =-12x^6+15x^4+8x^4-10x^2-28x^3+35x = \\[2ex] = \bm{-12x^6+23x^4-28x^3-10x^2+35x} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3) = \\[2ex] = 18x^9-36x^8-45x^7-8x^8+16x^7+20x^6+2x^7-4x^6-5x^5 = \\[2ex] = \bm{18x^9-44x^8-27x^7+16x^6-5x^5} \end{array}$

Ejercicio 5

Calcula las siguientes multiplicaciones de polinomios:

$\text{A)} \ (2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)$

$\text{B)} \ (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)$

$\text{C)} \ (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8)$

Ver solución

Para hacer un producto de 2 polinomios se tiene que multiplicar cada término del primer polinomio por cada término del segundo polinomio, y luego agrupar los monomios semejantes resultantes. Por tanto:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l}(2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)= \\[2ex] = 8x^6-12x^5+12x^5-18x^4-24x^4+36x^3+20x^3-30x^2-4x^2+6x = \\[2ex] = \bm{8x^6-42x^4+56x^3-34x^2+6x} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)= \\[2ex] =-x^5-5x^4+2x^3+9x^2+4x^4+20x^3-8x^2-36x-7x^3-35x^2+14x+63 = \\[2ex] = \bm{-x^5-x^4+15x^3-34x^2-22x+63} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8) = \\[2ex] = 8x^{13}-16x^{10}-2x^9+16x^7+24x^{11}-48x^8-6x^7+48x^5+ \\[2ex] + \ 12x^{10}-24x^7-3x^6+24x^4-20x^8+40x^5+5x^4-40x^2 = \\[2ex] = \bm{8x^{13}+24x^{11}-4x^{10}-2x^9-68x^8-14x^7-3x^6+} \\[2ex] \bm{+ \ 88x^5+29x^4-40x^2} \end{array}$

Ejercicio 6

Resuelve la siguiente multiplicación de 3 polinomios:

$(2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x)$

Ver solución

La operación del problema consta con 2 multiplicaciones de polinomios, concretamente está compuesta por dos binomios y un trinomio. Por lo que primero tenemos que solucionar un producto y luego multiplicar el resultado por el polinomio restante.

Así que calculamos la primera multiplicación:

$\begin{array}{l} (2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x) = \\[2ex] = \bigl[-10x^6+6x^4-12x^2+15x^4-9x^2+18 \bigr]\cdot (9x^3-6x) = \\[2ex] = (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)\end{array}$

Y ahora resolvemos la multiplicación que queda:

$\begin{array}{l} (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)= \\[2ex] = -90x^9+60x^7+189x^7-126x^5-189x^5+126x^3+162x^3-108x \\[2ex] =\bm{-90x^9+249x^7-315x^5+288x^3-108x} \end{array}$

Ejercicio 7

Multiplica los siguientes polinomios con coeficientes racionales (con fracciones):

$\displaystyle \left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right)$

Ver solución

Aunque los polinomios tengan fracciones, igualmente se trata de una multiplicación entre dos polinomios. De manera que se debe resolver como cualquier producto polinomial: multiplicando todos los elementos entre sí y después agrupando los monomios semejantes.

Entonces, multiplicamos los polinomios:

$\displaystyle \begin{array}{l} \displaystyle\left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right) = \\[4ex] = \displaystyle\frac{1}{3}x^2 \cdot 5x +\frac{1}{3}x^2\cdot \left(- \frac{2}{7} \right) -4x \cdot 5x - 4x \cdot \left(- \frac{2}{7} \right) = \\[4ex] =\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x\end{array}$

Y, para terminar, sumamos (o restamos) los términos cuyas partes literales son idénticas:

$\begin{array}{l}\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x= \\[4ex] \displaystyle= \frac{5}{3}x^3 -\frac{2}{21}x^2 -\frac{420}{21}x^2+\frac{8}{7} x \\[4ex] \displaystyle=\mathbf{\frac{5}{3}}\bm{x^3} -\mathbf{\frac{422}{20}}\bm{x^2}+\mathbf{\frac{8}{7}} \bm{x} \end{array}$

Para poder hacer bien este ejercicio era importante que dominases las operaciones con fracciones. Pero si te queda alguna duda de algún paso puedes preguntarla en los comentarios, que la responderemos tan rápido como podamos.

13 comentarios en “Multiplicación (o producto) de polinomios”

Lucía
03/05/2021 a las 04:36

Buenas noches. hice el ejercicio 7 y el término de grado 2 me da -422/21 x*2 y no como indica el resultado de ustedes, no logro hallar mi error

Responder
1. Polinomios
  06/05/2021 a las 11:21
  
  Sí Lucía, tienes razón. Había un 20 en el denominador de la fracción en lugar de un 21, había una errata de escritura.
  ¡Gracias por reportar el error!
2. Marilyn
  29/07/2021 a las 04:12
  
  Buenas noches me podrían ayudar con este ejercicio es que la verdad intento e intento y no logro hacerlo correctamente
  
  5m^4 – 3m^2 n^2 * 3m – n
3. Polinomios
  04/08/2021 a las 08:52
  
  Por supuesto Lucía, tienes resuelta el producto de polinomios a continuación:
  
  $\begin{array}{l}(5m^4 - 3m^2 n^2)\cdot (3m - n )=\\[2ex]=5m^4\cdot 3m+5m^4\cdot (-n)-3m^2n^2\cdot 3m - 3m^2n^2\cdot (-n)=\\[2ex] =15m^5-5m^4n-9m^3n^2+3m^2n^3\end{array}$
Bonnie
19/03/2022 a las 22:36

Muy buena página responde a los comentarios algo que no muchos hacen gracias por ayudar

Responder
1. Polinomios
  01/04/2022 a las 14:34
  
  ¡Muchas gracias Bonnie!
  
  Intento responder a todos los comentarios, pero últimamente están llegando muchos. Será buena señal. 🙂
Ana
18/06/2022 a las 00:12

Gracias me sirvió mucho este página….

Responder
1. Luz
  07/03/2023 a las 23:24
  
  Buenísimas explicaciones ! Me ha salvado el examen de mi hija para mañana ! ❤️
2. Polinomios
  08/03/2023 a las 10:42
  
  ¡Gracias Luz! ¡Seguro que le va genial el examen!
Luciana
05/10/2022 a las 19:57

Gracias me encanta esta pagina

Responder
1. Polinomios
  18/11/2022 a las 17:34
  
  ¡Muchas gracias Luciana!
Jesus
20/03/2023 a las 00:31

Buenas tardes me pueden ayudar con esta multiplicación por favor
-(3x -3x) ( 6x – 7x)

Responder
1. Polinomios
  25/03/2023 a las 21:39
  
  Sí claro Jesus, te dejo la multiplicación polinómica resuelta a continuación:
  $-(3x-3x)\cdot (6x-7x)$
  
  $(-3x+3x)\cdot (6x-7x)$
  
  $-3x\cdot 6x -3x\cdot (-7x)+3x\cdot 6x+3x\cdot (-7x)$
  
  $-18x^2+21x^2+18x^2-21x^2$
  
  $0$

Multiplicación de un polinomio por un número

Multiplicación de un polinomio por un monomio

Multiplicación de dos polinomios

Multiplicación de polinomios vertical

Propiedades de la multiplicación de polinomios

Ejercicios resueltos de multiplicaciones de polinomios

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Ejercicio 6

Ejercicio 7

13 comentarios en “Multiplicación (o producto) de polinomios”

Deja un comentario Cancelar respuesta