En esta página encontrarás cómo se hace la división de polinomios, tanto la división de un polinomio por un monomio como la división de un polinomio entre otro polinomio. También podrás ver ejemplos de divisiones de polinomios y practicar con ejercicios resueltos paso a paso. Y, además, hallarás las propiedades de esta operación polinómica.
Índice
División polinómica (o polinomial)
Antes de ver exactamente cómo se dividen dos polinomios vamos a repasar brevemente los conceptos de la división polinómica, para que así luego sea más fácil de entender el método que utilizaremos.
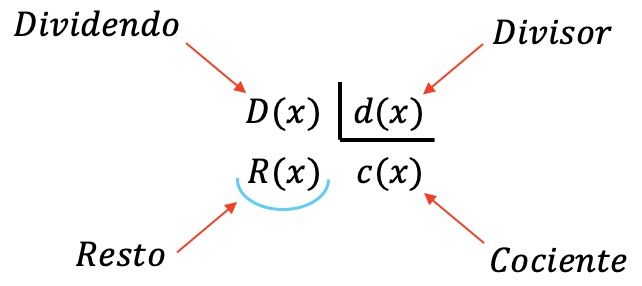
En una división polinomial intervienen 4 polinomios:
- Dividendo: el polinomio que es dividido.
- Divisor: el polinomio que divide al dividendo.
- Cociente: el resultado de la división del dividendo entre el divisor.
- Resto (o residuo): el polinomio que sobra al realizar la división entre los dos polinomios.
Por otro lado, también debes saber que existen dos tipos de división entre polinomios:
- División exacta de polinomios: una división entre polinomios es exacta cuando el resto es nulo. En tal caso, el polinomio dividendo es igual al divisor multiplicado por el cociente.
Además, en este caso el dividendo 
es un múltiplo del divisor 
y del cociente 
Del mismo modo, tanto el polinomio divisor como el polinomio cociente son divisores del dividendo.
- División entera de polinomios: en una división entera (o inexacta) de polinomios el resto es diferente de cero (0). Entonces, se cumple la propiedad fundamental de la división polinómica:
Ahora que ya hemos repasado qué es la división de polinomios, vamos a ver cómo dividir polinomios entre sí. En concreto, primero explicaremos la división entre un polinomio y un monomio y seguidamente la división entre 2 polinomios.
División de un polinomio entre un monomio
Antes de ver cómo se divide un polinomio por un monomio, primero vamos a recordar cómo se dividen los monomios entre sí, ya que es necesario saberlo para poder hacer este tipo de operación polinomial.
La división de dos monomios consiste en dividir sus coeficientes entre sí y sus partes literales entre sí, es decir, se dividen los coeficientes de los monomios y se restan los exponentes de las variables que tienen la misma base. Fíjate en el siguiente ejemplo:
Ahora sí, veamos en qué consiste la división de un polinomio por un monomio:
En matemáticas, para resolver la división de un polinomio entre un monomio se divide cada término del polinomio por el monomio.
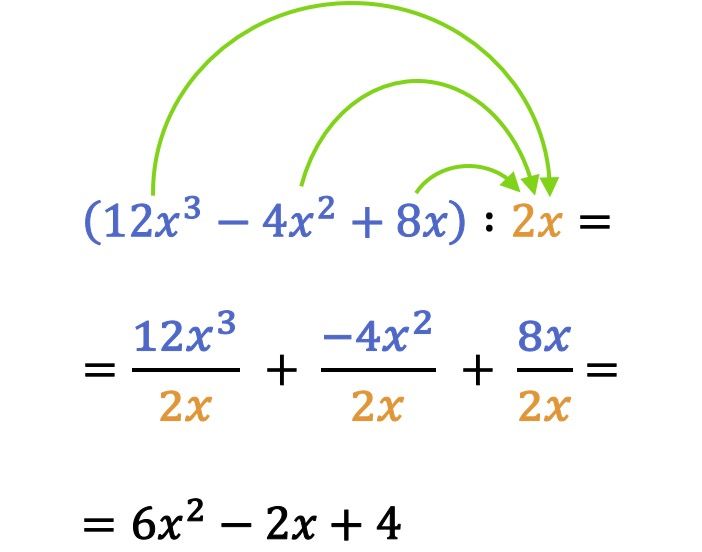
Fíjate en el ejemplo de la división anterior que cuando dividimos monomios o polinomios también hay que tener en cuenta la regla de los signos. De hecho, un error muy típico de las divisiones entre polinomios y monomios es equivocarse por el signo de un término.
División de un polinomio entre otro polinomio
Para dividir dos polinomios se debe de seguir un procedimiento, así que vamos a ver cómo es el método de la división de polinomios, también llamado división larga de polinomios, resolviendo un ejemplo paso a paso:
- Calcula el resultado de dividir el polinomio
entre el polinomio 
Siendo los dos polinomios:
Lo primero que debemos hacer es colocar los polinomios en forma de división. A la izquierda escribimos el numerador de la fracción (polinomio dividendo) y a la derecha ponemos el denominador de la fracción (polinomio divisor):
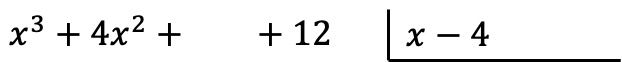
Atención: Si un un polinomio no tiene un monomio de un determinado grado, tenemos que dejar un hueco en su lugar. Por ejemplo, el polinomio 
no tiene término de grado 1, por eso hay un espacio en blanco en su lugar.
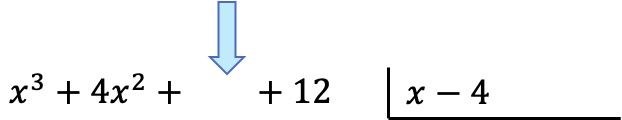
Una vez hemos puesto los polinomios en su sitio, vamos a hallar el cociente. Y para encontrar el primer término del cociente tenemos que dividir el primer término del dividendo entre el primer término del divisor:
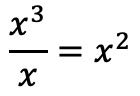
Y ponemos el resultado de la división en el lugar del cociente:
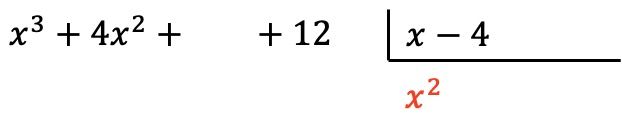
Ahora multiplicamos el término encontrado por cada elemento del divisor, y cada resultado lo ponemos debajo del dividendo en su columna correspondiente cambiándole de signo:
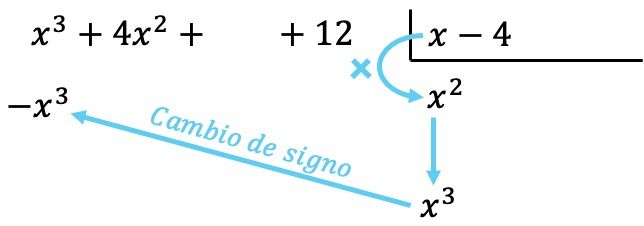
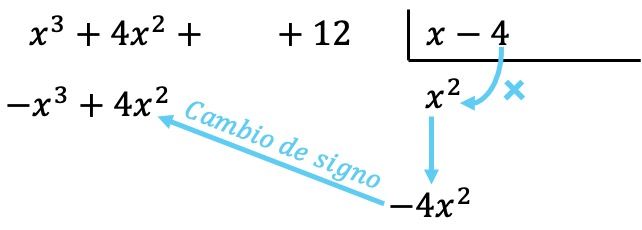
Como sucede en todas las operaciones con polinomios, es importante ordenar los polinomios de mayor a menor grado de manera que todos los términos de un mismo grado estén situados en una misma columna.
Una vez hemos colocado los resultados de las multiplicaciones con el signo contrario, debemos sumar los términos que están alineados verticalmente:
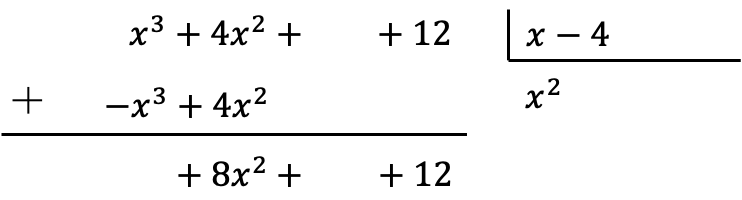
Fíjate que al hacer esta suma el coeficiente de mayor grado se anula y, por tanto, tenemos un término menos en el dividendo.
Ahora tenemos que ir repitiendo el mismo procedimiento hasta que el polinomio dividendo sea de menor grado que el polinomio divisor.
De modo que dividimos el primer término del dividendo entre el primer término del divisor:
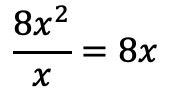
Colocamos el resultado en el cociente:
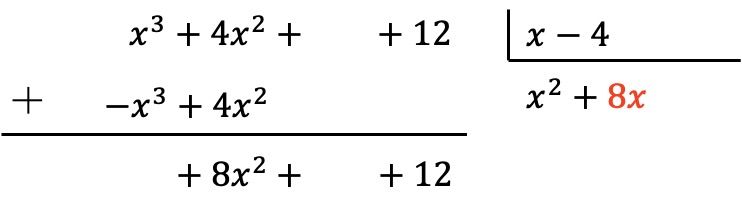
Igual que antes, multiplicamos el nuevo término del cociente por cada elemento del divisor y ponemos los resultados con el signo contrario en las columnas correspondientes del dividendo:
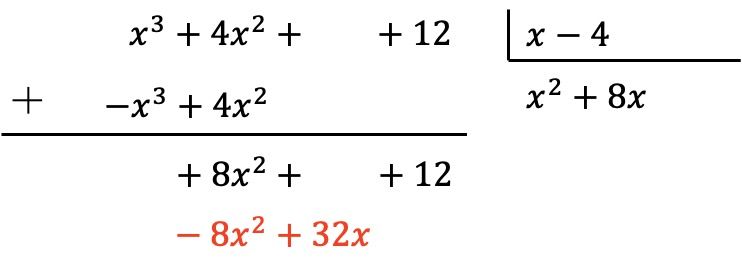
Y sumamos verticalmente:
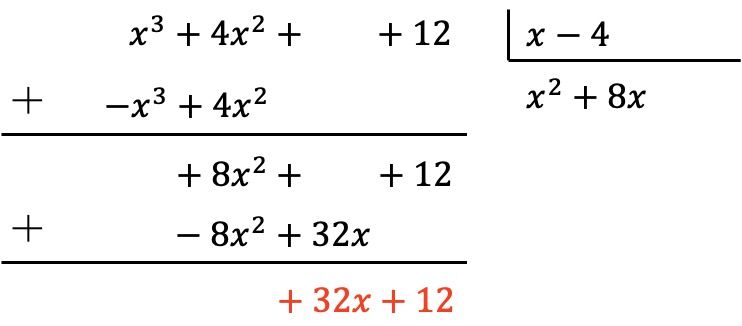
El polinomio dividendo aún no es de menor grado que el polinomio divisor, por lo que debemos seguir haciendo el mismo proceso.
Así que primero dividimos el primer término del dividendo entre el primer término del divisor, en segundo lugar multiplicamos el resultado por cada término del divisor, luego ponemos los resultados cambiados de signo en el dividendo y, finalmente, sumamos verticalmente:
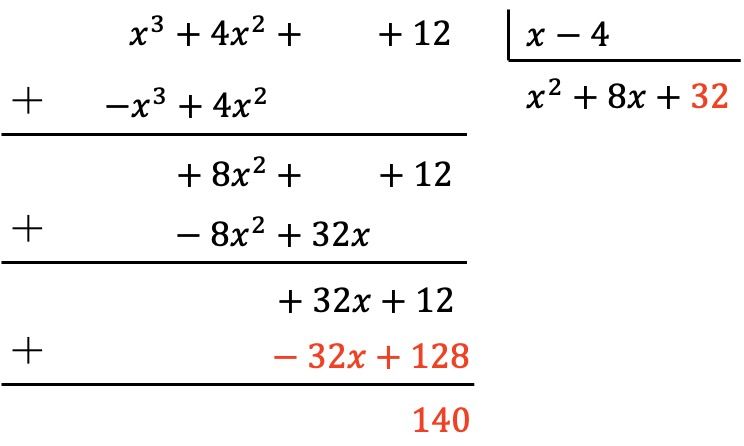
De manera que ya hemos conseguido que el polinomio dividendo sea de grado inferior que el grado del divisor, porque el dividendo es de grado 0 y el divisor de grado 1. En consecuencia, la división queda terminada.
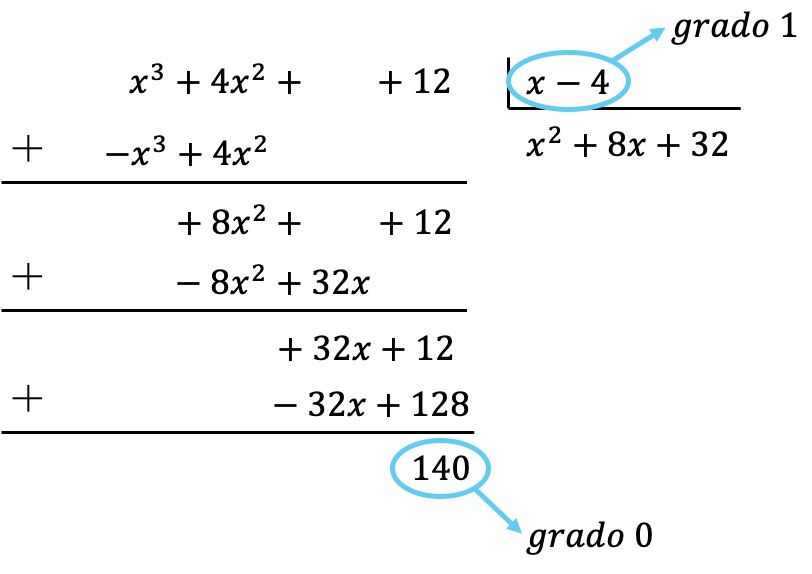
Así que el resultado de la división es:
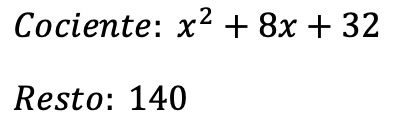
Por otra parte, podemos comprobar que hemos hecho bien la división polinómica a partir de la condición fundamental de la división de polinomios:
✅
La ecuación se cumple, por lo tanto, la división polinómica se ha realizado correctamente.
De forma que ya hemos acabado la división de polinomios, esperamos que te hayamos podido ayudar con esta explicación. ¿Qué te ha parecido el método de la división de polinomios? ¿Tienes alguna duda? ¿Te gusta? ¿O preferirías que no existiesen las divisiones polinómicas? 😂 ¡Os leemos en los comentarios! 👇👇👇
Propiedades de la división de polinomios
Cualquier división de polinomios cumple con las siguientes características:
✓ El grado del polinomio dividendo siempre debe ser superior al grado del polinomio divisor.
✓ El grado del polinomio dividendo es equivalente a la suma de los grados del divisor y del cociente.
✓ El grado del resto siempre es menor que el grado del divisor (y por tanto también del dividendo).
✓ El dividendo es igual al producto del divisor por el cociente más el resto. Esta condición también se cumple en la división de números.
Ejercicios resueltos de la división de polinomios
Ejercicio 1
Determina el resultado de la siguiente división de un polinomio entre un monomio:
Para dividir un polinomio entre un monomio tenemos que resolver la división de cada término del polinomio entre dicho monomio:
![\begin{aligned} \left(15x^5+9x^3 \right) : \left(3x^2\right) & = \cfrac{15x^{5}}{3x^2}+ \cfrac{9x^3}{3x^2} \\[2ex] & = \bm{5x^3+3x} \end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-cf8e7cc1b6aa9b99dc3cc4944c00b8db_l3.svg "Rendered by QuickLaTeX.com")
Recuerda que en la division entre monomios se dividen los coeficientes entre sí y se restan los exponentes de las potencias cuya base es igual.
Ejercicio 2
Calcula la siguiente división de un polinomio entre un monomio:
Para dividir un polinomio entre un monomio tenemos que hacer la división de cada término del polinomio entre dicho monomio:
![\begin{aligned} \left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right) & = \cfrac{16x^5}{4x^2}+ \cfrac{-4x^3}{4x^2} + \cfrac{-20x^2}{4x^2} \\[2ex] & = \bm{4x^3-x-5} \end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-89ab929ce3b637f87f608d8f6d3183d7_l3.svg "Rendered by QuickLaTeX.com")
Recuerda que en la division monomial se dividen los coeficientes entre sí y se restan los exponentes de las potencias cuya base es equivalente.
Ejercicio 3
Resuelve la siguiente división de un polinomio entre un monomio:
Para dividir un polinomio entre un monomio tenemos que resolver la división de cada término del polinomio entre dicho monomio:
![\begin{aligned} \left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right) & = \cfrac{12x^{10}}{-6x^3}+ \cfrac{-30x^{7}}{-6x^3} + \cfrac{-18x^6}{-6x^3} + \cfrac{54x^4}{-6x^3} \\[2ex] & = \bm{-2x^7+5x^4+3x^3-9x} \end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-3d8069d42e5cd5044a85538dfe5b4834_l3.svg "Rendered by QuickLaTeX.com")
Ten en cuenta que el monomio divisor es negativo y, por tanto, cambian los signos de todas las divisiones.
Ejercicio 4
Efectúa la siguiente división de polinomios:
Para realizar la división de polinomios debemos aplicar el método explicado más arriba:
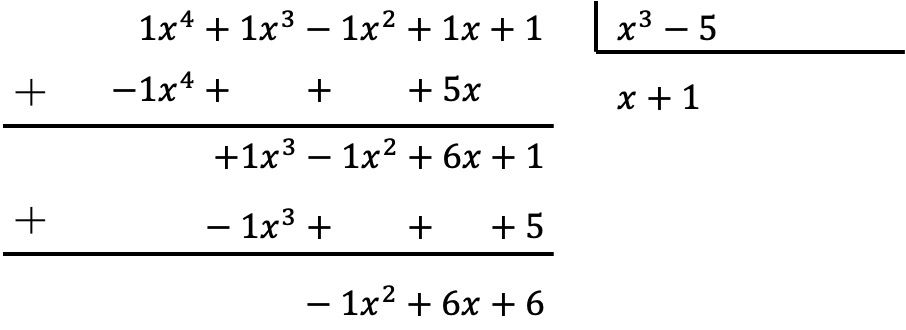
De modo que el resultado de la división entre los dos polinomios es:
Cociente: 
Resto: 
Ejercicio 5
Calcula la siguiente división de polinomios:
Para solucionar la división del polinomio entre el binomio debemos aplicar el método que hemos visto más arriba:
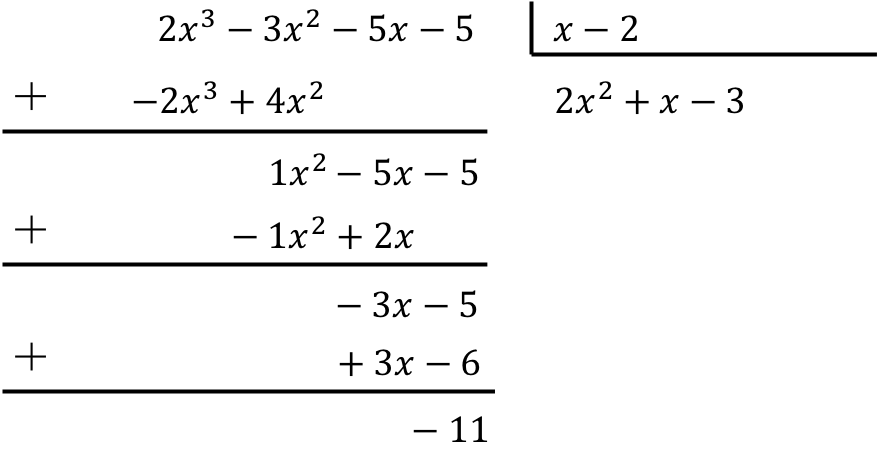
Con lo que el resultado de la división polinomial es:
Cociente: 
Resto: 
Ejercicio 6
Resuelve la siguiente división de polinomios:
Para calcular la división de polinomios debemos aplicar el método explicado:
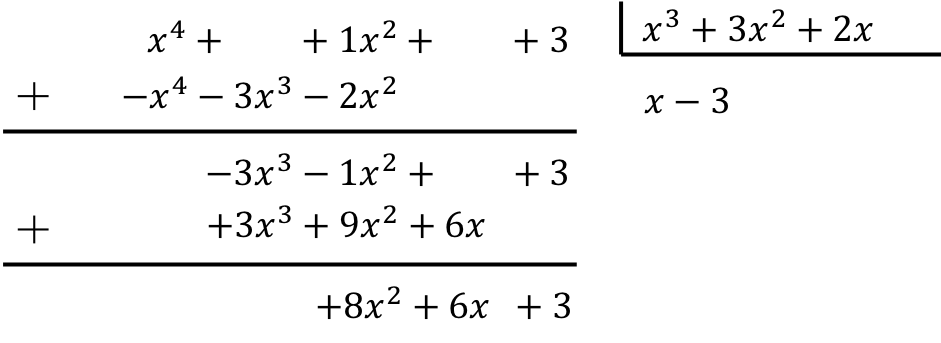
De manera que el resultado de la división entre los dos polinomios es:
Cociente: 
Resto: 
Ejercicio 7
Halla el resultado de la siguiente división entre 2 polinomios:
Para calcular la división del polinomio entre el trinomio debemos aplicar el método explicado:
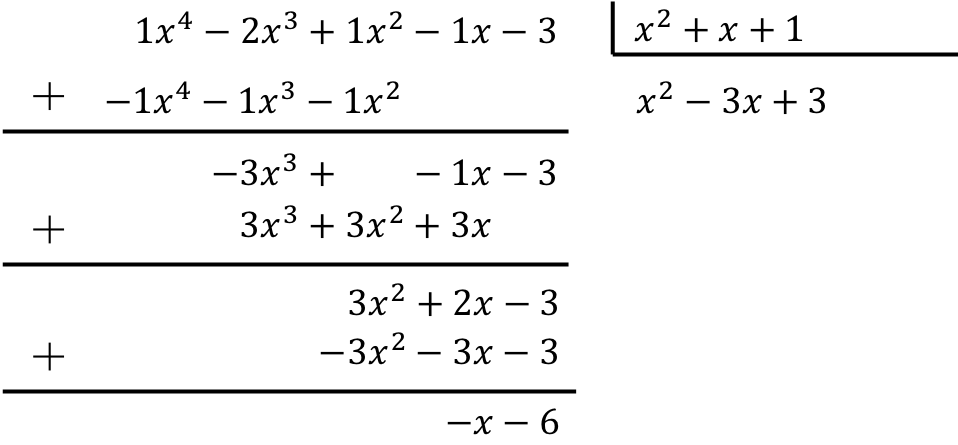
De manera que el resultado de la división entre los dos polinomios es:
Cociente: 
Resto: 
👉👉👉Si has llegado hasta aquí significa que ya sabes cómo se dividen los polinomios. ¡Genial! Ahora que ya dominas las divisiones de polinomios, debes saber que existe un método que permite resolver mucho más rápido algunas divisiones entre polinomios. Se trata de la división sintética o regla de Ruffini, puedes ver cómo se aplica este truco y cuándo se puede utilizar haciendo click en el enlace.😉
Agradecida infinitamente, he recordado mis años de estudiante. Hoy día cuento con 61 años de edad y ayudo a los adolescentes en esta pandemia a realizar sus actividades. No recuerdo tantas cosas.
¡Genial Inowa! Cualquier duda que tengas, aquí tienes tu página de confianza 😉
Holaaaa, tus resúmenes son excelentes!!! Por fin entiendo las matemáticas. Muchas gracias
¡Me alegro Vera de que te ayude esta web! ¡Muchas gracias!