División de monomios

En esta página explicamos cómo se hace la división de monomios. Además, podrás ver ejemplos de divisiones de monomios e incluso practicar con ejercicios resueltos paso a paso.

¿Cómo se realiza la división de monomios?

En matemáticas, el resultado de la división de monomios es otro monomio cuyo coeficiente equivale al cociente de los coeficientes de los monomios y cuya parte literal se obtiene de dividir las variables que tienen la misma base, es decir, restando sus exponentes.

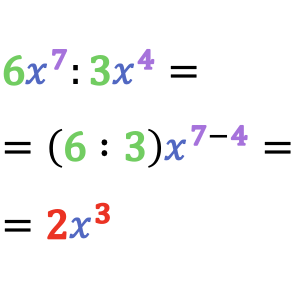
qué es la división de monomios

Por lo tanto, para dividir dos monomios diferentes simplemente dividimos los coeficientes entre sí y restamos los exponentes de las potencias que tengan la misma base.

Evidentemente, cualquier división de monomios también se puede expresar en forma de fracción:

8x^3y^2z : 2x^2y = \cfrac{8x^3y^2z}{2x^2y} = 4xyz

Por último, debes recordar que en la división de los coeficientes de los monomios también se aplica la regla (o ley) de los signos, ya que la división algebraica de monomios consiste en una operación aritmética. Por lo tanto:

  • Un monomio positivo dividido entre otro monomio positivo es igual a un monomio positivo:

8x^9: 2x^3 = 4x^6

  • Un monomio positivo entre un monomio negativo (o viceversa) es equivalente a un monomio negativo:

-8x^9: 2x^3 = -4x^6

8x^9: (-2x^3) = -4x^6

  • Dos monomios negativos divididos entre sí da como resultado un monomio positivo:

-8x^9: (-2x^3) = 4x^6

Ejemplos de divisiones de monomios

Para que puedas entender del todo cómo se dividen dos o más monomios, a continuación te dejamos con varios ejemplos de la división entre monomios:

  • 7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2
  • 12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3
  • 15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y
  • 27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5
  • -18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2

Ahora que has visto cómo se calcula la división entre dos monomios, seguramente también te interese saber cómo se hace la división de un polinomio entre un monomio. Esta operación es más difícil, pero en esta página se explica paso a paso y, además, podrás practicar con ejercicios resueltos, de manera que seguro que lo entiendes. 👍👍

Ejercicios resueltos de la división de monomios

A continuación tienes varios ejercicios resueltos paso a paso de divisiones de monomios para que puedas practicar más:

Ejercicio 1

Calcula las siguientes divisiones de monomios:

\text{A)} \ 24x^4: 6x^2

\text{B)} \ 16y^9: (-2y^6)

\text{C)} \ 32x^7:4x^3

\text{D)} \ -21a^3:(-3a)

\text{A)} \ 24x^4: 6x^2 = (24:6)x^{4-2} = \bm{4x^2}

\text{B)} \ 16y^9: (-2y^6)= (16:(-2))y^{9-6} = \bm{-8y^3}

\text{C)} \ 32x^7:4x^3 = (32:4)x^{7-3}= \bm{8x^4}

\text{D)} \ -21a^3:(-3a) = (-21:(-3))a^{3-1} = \bm{7a^2}

Fíjate que cuando una variable no tiene exponente significa que está elevado a la 1. Por tanto, en la última operación el término -3a es equivalente a -3a^1 y por eso mismo debemos restar una unidad en el exponente del resultado.

 

Ejercicio 2

Resuelve las siguientes divisiones de monomios:

\text{A)} \ 14x^8y^3 :2x^6y

\text{B)} \ 45x^{11}y^9z^5 : (-5x^6y^2z^3)

\text{C)} \ -11a^5b^9 : (-a^2b^6)

\text{D)} \ 42x^5y^3z^6 : 7x^2y^3z^4

\text{A)} \ 14x^8y^3 :2x^6y = \bm{7x^2y^2}

\text{B)} \ 45x^{11}y^9z^5 : (-5x^6y^2z^3)= \bm{-9x^5y^7z^2}

\text{C)} \ -11a^5b^9 : (-a^2b^6) = \bm{11a^3b^3}

\text{D)} \ 42x^5y^3z^6 : 7x^2y^3z^4= 6x^3y^0z^2=\bm{6x^3z^2}

En la última operación hemos simplificado el término y^0 porque cualquier número elevado a 0 es igual a 1. Por lo tanto:

6x^3y^0z^2=6x^3\cdot 1 \cdot z^2=\bm{6x^3z^2}

 

Ejercicio 3

Simplifica al máximo las siguientes divisiones de monomios:

\text{A)} \ 36x^7y^9z^2 : 6x^2y^4 : 3x^4y^2z

\text{B)} \ -50a^{12}b^8c^9: (-5a^5b^3c^2) : (-2a^4b^2c^4)

\text{C)} \ 30x^5y^9z^8 : 2xy^4z^6 :(-3x^2y^3z)

\text{D)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)

\text{A)} \ 36x^7y^9z^2 : 6x^2y^4 : 3x^4y^2z = 6x^5y^5z^2: 3x^4y^2z = \bm{2xy^3z}

\text{B)} \ -50a^{12}b^8c^9: (-5a^5b^3c^2) : (-2a^4b^2c^4) = 10a^7b^5c^7: (-2a^4b^2c^4) = \bm{-5a^3b^3c^3}

\text{C)} \ 30x^5y^9z^8 : 2xy^4z^6 :(-3x^2y^3z) = 15x^4y^5z^2:(-3x^2y^3z) = \bm{-5x^2y^2z}

\text{D)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)= -8x^4y^4z^6: (-4x^2y^2z^3)= \bm{2x^2y^2z^3}

 

Si estás más interesad@ en la división de monomios y polinomios, te recomendamos que le eches un vistazo a la regla de Ruffini. Porque es un método que permite simplificar algunas divisiones y, por tanto, te permite ahorrar mucho tiempo e ir más rápido.

12 comentarios en “División de monomios”

    3. Polinomios

      Buenas Nicole,

      Para dividir dos monomios debes dividir sus coeficientes entre sí y restar los exponentes de las variables que sean iguales. Por tanto:
      35c^4d^2f^3:7f^2dc^4=5c^0d^1f^1=5df

    4. Anlennis

      Yo aprendi que para la división de monomios solo tenemos que dividir los coeficientes entre sí y restar los exponentes.

      Gracias por la explicación excelente

    1. Polinomios

      Hola Andra,

      Esta operación es una división entre dos polinomios, así que para resolverla debes seguir otro procedimiento. Puedes ver cómo se hace en nuestro post de la división de polinomios.

    1. Polinomios

      Hola Michele,

      En este caso no puedes hacer la división de monomios, es decir, no se puede simplificar más. Porque no hay ningún término repetido o múltiple en el numerador y el denominador de la fracción.

  4. Fernando

    Muchas gracias a la persona/personas que escribieron toda esta información desde suma/resta/multiplicacion y división, los temas estan bien explicados y son faciles de entender, muy buen trabajo por parte de la pagina, sigan asi👌❤

    Responder
    1. Polinomios

      ¡Muchísimas gracias por tu comentario Fernando! ¡Felicitaciones así te motivan aún más!

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio