▷ Trinomio: qué es, tipos, fórmulas, ejemplos...

En esta página encontrarás la explicación de qué es un trinomio. También, podrás ver los diferentes tipos de trinomios que hay y, además, todas las fórmulas que hay relacionadas con los trinomios.

Índice

¿Qué es un trinomio?

En matemáticas, la definición de trinomio es la siguiente:

Un trinomio es un polinomio formado solamente por tres monomios. Es decir, un trinomio es una expresión algebraica con únicamente 3 términos diferentes que están unidos por el signo más (+) o el signo menos (-).

La palabra trinomio proviene del griego y está compuesta por dos componentes léxicos (tri y nomos), que significan lo siguiente:

tri: prefijo que significa 3.
nomos: quiere decir parte.

De ahí se puede deducir el significado de trinomio: polinomio con tres partes (o tres monomios).

Por otra lado, debes saber que en muchas ocasiones es muy útil factorizar un trinomio. Y para hacer la factorización de un polinomio existen varios procedimientos como por ejemplo el método de multiplicación FOIL o la regla de Ruffini, pero cuando es un trinomio se hace más rápido resolviendo una ecuación. Descubre este método en cómo factorizar polinomios de grado 2.

Ejemplos de trinomios

Para acabar de entender el concepto de un trinomio, vamos a ver varios ejemplos de este tipo de polinomio:

Ejemplo de un trinomio de segundo grado:

$x^2-5x+6$

Ejemplo de un trinomio de tercer grado:

$x^3+4x^2+1$

Ejemplo de un trinomio de cuarto grado:

$-3x^4+x^2-8x$

Ahora que ya sabemos en qué consiste un trinomio, vamos a ver los diferentes tipos que hay y cómo resolver operaciones con trinomios de manera fácil mediante fórmulas.

Trinomio cuadrado perfecto

Un trinomio cuadrado perfecto, por brevedad también llamado TCP, es el trinomio que se obtiene de elevar un binomio al cuadrado, ya sea un binomio suma o un binomio resta.

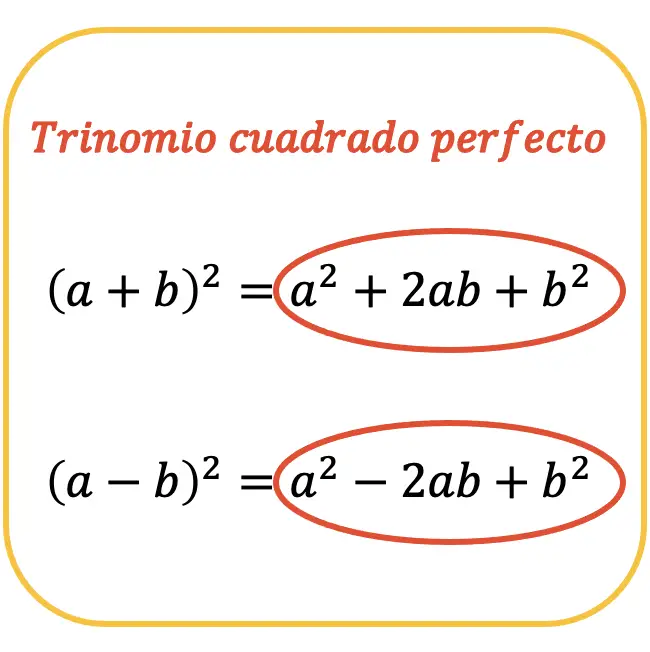
Por lo tanto, un trinomio cuadrado perfecto consiste en un polinomio con dos cuadrados perfectos (su raíz cuadrada es exacta), y otro término que es el doble producto de las bases de esos dos cuadrados cuyo signo puede ser positivo o negativo.

Por otra parte, hay que tener en cuenta que tanto el cuadrado de una suma como el cuadrado de una diferencia son identidades notables (o productos notables), por lo que se trata de dos fórmulas muy utilizadas en matemáticas.

Ejemplo:

$x^2+6x+9$

Este ejemplo es un trinomio cuadrado perfecto porque en su expresión algebraica hay dos cuadrados perfectos, porque las raíces cuadradas de $x^2$ y de 9 son exactas:.

$\sqrt{x^2}=x$

$\sqrt{9}=3$

Y, además, el último término restante del trinomio $(6x)$ se obtiene multiplicando las bases de los dos cuadrados anteriores entre sí y por 2:

$2\cdot x \cdot 3 = 6x$

De modo que toda la identidad notable completa en este ejercicio sería:

$x^2+6x+9 =(x+3)^2$

Si te fijas bien, lo que acabamos de hacer es factorizar un trinomio cuadrado perfecto, porque hemos logrado descomponer en factores la expresión del trinomio. Así pues, estas fórmulas te servirán para hacer la factorización de un trinomio cuadrado perfecto, pero si estás interesad@ en factorizar cualquier otro tipo de trinomio te recomendamos que le eches un vistazo al enlace de más arriba en el apartado de qué es un trinomio (cómo factorizar polinomios de grado 2).

Trinomio al cuadrado

La fórmula que sirve para calcular la potencia de un trinomio elevado al cuadrado es la siguiente:

Un trinomio elevado al cuadrado es igual al cuadrado del primer término, más el cuadrado del segundo término, más el cuadrado del tercer término, más el doble del primero por el segundo, más el doble del primero por el tercero, más el doble del segundo por el tercero.

Veamos un ejemplo de cómo se calcula el cuadrado de un trinomio:

Ejemplo:

Calcula el siguiente trinomio elevado a la 2:

$\left(x^2+x+3\right)^2$

La fórmula del cuadrado de un trinomio es:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

De modo que primero tenemos que identificar los valores de los parámetros $a,b$ y $c$ de la fórmula. En este ejercicio $a$ es $x^2,$ el coeficiente $b$ corresponde a la $x,$ y $c$ es el término independiente 3:

$\left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}$

Y cuando ya sabemos los valores, simplemente tenemos que sustituir dichos valores en la fórmula y hacer los cálculos:

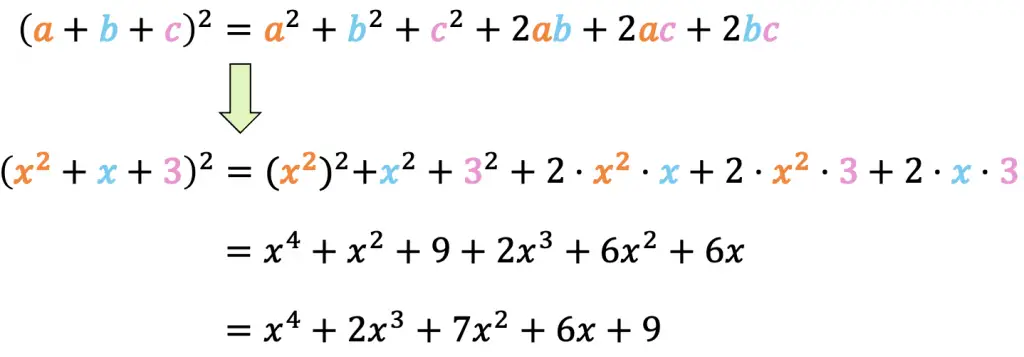
ejemplo de un trinomio elevado al cuadrado

Trinomio al cubo

La fórmula que permite hallar la potencia de un trinomio elevado al cubo es la siguiente:

Por ejemplo, si queremos calcular el siguiente trinomio elevado a la 3:

$\left(x^2+5x-3\right)^3$

Debemos utilizar la fórmula del cubo de un trinomio:

$(a+b+c)^3 = a^3+b^3+c^3+3(a+b)(a+c)(b+c)$

Por tanto, la solución del problema sería:

$\begin{aligned}\left(x^2+5x-3\right)^3 & = \left(x^2\right)^3+(5x)^3+(-3)^3+3\left(x^2+5x\right)\left(x^2+(-3)\right)\bigl(5x+\left(-3\right)\bigr) \\[2ex] & = x^6+125x^3-27+3\left(x^4+5x^3-3x^2-15x\right)\bigl(5x-3\bigr)\\[2ex] & = x^6+125x^3-27+3\left(5x^5+22x^4-30x^3-66x^2+45x\right) \\[2ex] & = x^6+125x^3-27+15x^5+66x^4-90x^3-198x^2+135x \\[2ex] & = \bm{x^6+15x^5+66x^4+35x^3-198x^2+135x-27}\end{aligned}$

Trinomio de segundo grado

En álgebra, el trinomio de segundo grado con una variable se puede resolver con la famosa fórmula de la ecuación de segundo grado, que es:

$ax^2+bx+c=0$

$x=\cfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

A continuación, vamos a solucionar un ejercicio de un trinomio de segundo grado a modo de ejemplo:

$x^2-2x-3=0$

Efectivamente, se trata de un trinomio de segundo grado. Por lo tanto, tenemos que aplicar la fórmula de la ecuación de segundo grado:

$x=\cfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Ahora tenemos que identificar el valor cada incógnita: $a$ es el coeficiente del monomio de mayor grado que en este caso es 1, $b$ corresponde al coeficiente del término intermedio que es -2, y, finalmente, $c$ representa el término independiente que es -3.

$a=1 \qquad b=-2 \qquad c=-3$

Entonces, aplicamos la fórmula sustituyendo los valores hallados en ella:

$x=\cfrac{-(-2) \pm \sqrt{(-2)^2 - 4\cdot 1 \cdot (-3)}}{2\cdot 1}$

Y, por último, calculamos las operaciones:

$\displaystyle x=\cfrac{+2 \pm \sqrt{4 +12}}{2} = \cfrac{2\pm \sqrt{16}}{2} = \cfrac{2 \pm 4}{2} = \begin{cases} \cfrac{2+4}{2}=3 \\[4ex] \cfrac{2-4}{2} = -1 \end{cases}$

Así que las soluciones de la ecuación de segundo grado son:

$x = 3 \qquad x=-1$

¿Qué es un trinomio?

Ejemplos de trinomios

Trinomio cuadrado perfecto

Ejemplo:

Trinomio al cuadrado

Ejemplo:

Trinomio al cubo

Trinomio de segundo grado

Deja un comentario Cancelar respuesta