Monomios

Aquí explicamos todo lo que debes saber sobre los monomios: qué son, cuáles son sus partes (y cómo identificarlas), los diferentes tipos de monomios que hay, cómo calcular operaciones con monomios, el valor numérico de un monomio,… Además, podrás ver ejemplos y ejercicios resueltos paso a paso de monomios.

¿Qué son los monomios?

En matemáticas, la definición de un monomio es la siguiente:

Un monomio es una expresión algebraica formada por una combinación de números y letras. En concreto, un monomio está compuesto por el producto entre un número y una o más variables (letras) elevadas a exponentes.

Por ejemplo, el término 7x³y² se trata de un monomio porque tiene un número (7) y diferentes letras (x, y).

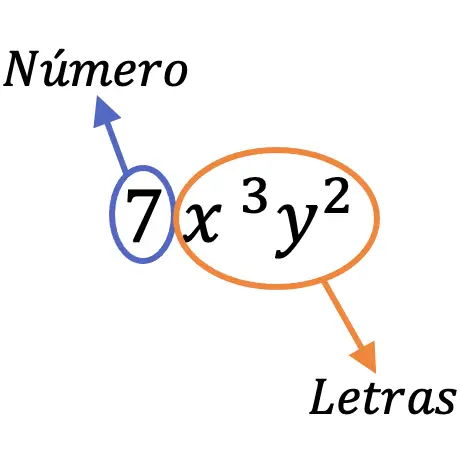
Partes de un monomio

Ahora que hemos visto el significado de un monomio, veamos cuáles son todas las partes de un monomio:

• Coeficiente: es el número que está multiplicando a las variables (o letras) del monomio.
• Variable: es cada una de las letras que aparecen en el monomio.
• Parte literal: corresponde a todas las variables que componen el monomio junto con todos sus respectivos exponentes.
• Grado: consiste en la suma de todos los exponentes de las letras que forman el monomio.

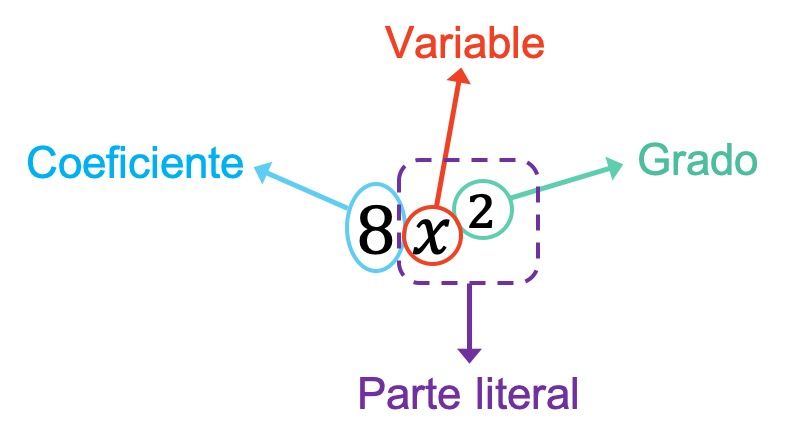
El coeficiente del monomio del ejemplo de arriba es 8 ya que es el número que está multiplicando a las variables. Además, en este caso el monomio solo tiene una variable, que es x. Así que la parte literal del monomio está formada por esa variable más su exponente, esto es x². Finalmente, el grado del monomio es 2 porque es el único exponente que posee.

Intenta ahora resolver tú el siguiente ejercicio sobre las partes de un monomio:

• Identifica todas las partes del siguiente monomio:

Los componentes del monomio del enunciado son:

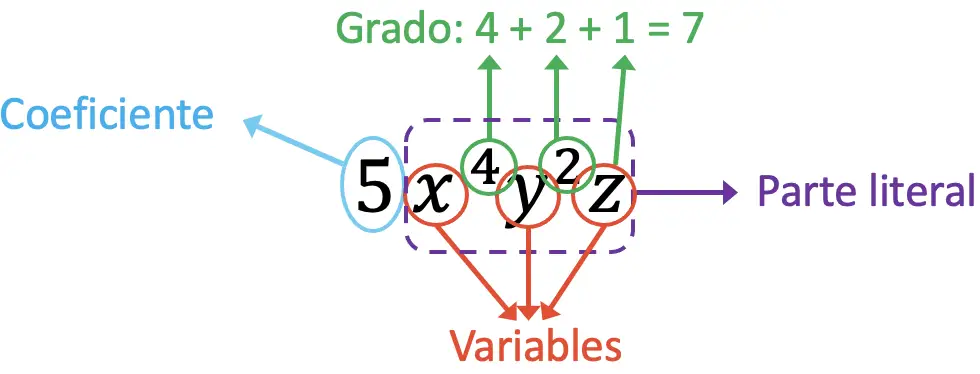
El coeficiente del monomio del problema es 5, ya que es el término que multiplica a las letras. Por otra parte, las variables de este monomio son x, y, z. En tercer lugar, la parte literal del monomio corresponde a la expresión x⁴y²z. Y, por último, el grado del monomio es igual a la suma de todos los exponentes de las variables, es decir 7 (4+2+1=7).

Fíjate que cuando una letra no tiene exponente en realidad significa que tiene un 1 como exponente. Por eso para calcular el grado del monomio del problema hemos sumado una unidad que representa el exponente de la variable z.

 

Tipos de monomios

Existen diferentes tipos de monomios, cada uno con sus propiedades. Los monomios más importantes son los monomios semejantes, los monomios homogéneos, los monomios heterogéneos y los monomios opuestos. A continuación, veremos las características de cada tipo.

Monomios semejantes

Los monomios semejantes son aquellos monomios que tienen la misma parte literal. Por lo tanto, dos o más monomios son semejantes cuando poseen las mismas letras y los mismos exponentes.

Por ejemplo, los siguientes dos monomios son semejantes porque, aunque tienen distinto coeficiente, están formados por las mismas variables y están elevadas a los mismos exponentes.

Como veremos más abajo, este tipo de monomios sirven para resolver operaciones de monomios.

Monomios homogéneos

Dos monomios son homogéneos cuando su grado absoluto es equivalente.

Por ejemplo, los siguientes dos monomios son homogéneos porque el grado de ambos es igual a 5:

El primero monomio tiene una sola variable que está elevada a la 5, por lo que su grado es 5. Y el segundo polinomio tiene una variable elevada al cuadrado y otra elevada al cubo, de forma que su grado también es 5 (2+3=5).

Como puedes ver, para que dos monomios sean homogéneos no hace falta que tengan la misma parte literal, sino que solamente es necesario que tengan el mismo grado absoluto.

Monomios heterogéneos

Los monomios heterogéneos son los monomios que no tienen el mismo grado absoluto. Es decir, los monomios heterogéneos son el contrario de los monomios homogéneos.

Los siguientes 3 monomios son heterogéneos debido a que cada uno presenta un grado diferente:

El primer monomio es de grado 8, el segundo monomio es de grado 2, y el tercer monomio es de grado 11. Por lo tanto, los tres monomios son heterogéneos entre sí.

Monomios opuestos

Los monomios opuestos son aquellos monomios que son homogéneos (tienen la misma parte literal) y, además, sus coeficientes son opuestos, es decir, sus coeficientes tienen el mismo valor pero de signo contrario.

Por ejemplo, los siguientes dos monomios son opuestos:

Los dos anteriores monomios son opuestos porque únicamente se diferencian en su signo, el primero es de signo positivo y el segundo tiene signo negativo.

Ahora que ya has visto varios ejemplos de monomios, puede que te interese saber otra expresión algebraica similar: el binomio. De hecho, un binomio está compuesto por la suma (o resta) de varios monomios, así que resulta interesante ver la relación entre estos dos conceptos. Puedes ver cuál es el significado de binomio haciendo click en este enlace.

Operaciones con monomios

Para profundizar más en el concepto de monomio, vamos a ver qué operaciones se pueden hacer con los monomios. En particular, los monomios se pueden sumar, restar, multiplicar, dividir y potenciar. Y cada tipo de operación tiene sus peculiaridades, así que a continuación las analizamos una a una por separado.

Suma de monomios

Dos o más monomios solo se pueden sumar si son monomios semejantes. Entonces, la suma de dos monomios semejantes es igual a otro monomio compuesto por la misma parte literal y la suma de los coeficientes de esos dos monomios.

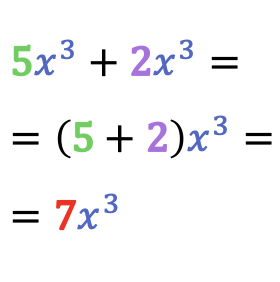
Ejemplos de sumas de monomios

• 
• 
• 
• 
• 

Si quieres practicar de hacer ejercicios de sumas de monomios puedes buscarlos en el buscador de arriba a la derecha, ya que tenemos toda una página llena con ejercicios resueltos de sumas de monomios.

Resta de monomios

Dos o más monomios solo se pueden restar si son monomios semejantes. Así pues, la resta de dos monomios semejantes es igual a otro monomio compuesto por la misma parte literal y la resta de los coeficientes de esos dos monomios.

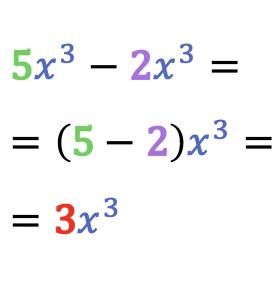
Ejemplos de restas de monomios

• 
• 
• 
• 
• 

Puedes practicar con los ejercicios resueltos paso a paso de restas de monomios que hay en nuestra web. Los puedes encontrar a través del buscador de arriba a la derecha.

Multiplicación de monomios

El resultado de la multiplicación de dos monomios es otro monomio cuyo coeficiente es el producto de los coeficientes de los monomios y cuya parte literal se obtiene de multiplicar las variables que tienen la misma base, es decir, sumando sus exponentes.

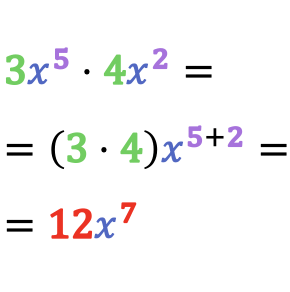
De manera que para resolver el producto entre dos monomios diferentes se deben multiplicar los coeficientes entre sí y sumar los exponentes de las potencias que tengan la misma base.

Por contra, si multiplicamos dos monomios con alguna potencia de base distinta, simplemente tenemos que multiplicar sus coeficientes entre sí y dejar las potencias igual:

Ejemplos de multiplicaciones de monomios

• 
• 
• 
• 
• 

Para practicar con ejercicios resueltos paso a paso de multiplicaciones de monomios puedes ir al artículo que tenemos en esta web. Lo encontrarás fácilmente con el buscador de arriba a la derecha.

División de monomios

El resultado de la división de monomios es otro monomio cuyo coeficiente equivale al cociente de los coeficientes de los monomios y cuya parte literal se obtiene de dividir las variables que tienen la misma base, esto es, restando sus exponentes.

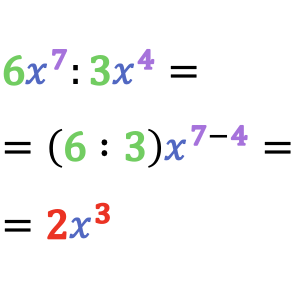
De modo que para dividir dos monomios diferentes simplemente dividimos los coeficientes entre sí y restamos los exponentes de las potencias que tengan la misma base.

Ejemplos de divisiones de monomios

• 
• 
• 
• 
• 

Las divisiones de monomios son más difíciles de lo que parecen, así que te recomendamos que intentes hacer los ejercicios resueltos paso a paso que tenemos de divisiones de monomios. La manera más rápida de hallarlos es a través de nuestro buscador de arriba a la derecha.

Potencia de un monomio

Para calcular la potencia de un monomio se debe elevar cada elemento del monomio al exponente de la potencia. Es decir, la potencia de un monomio consiste en elevar su coeficiente y sus variables (letras) al exponente de la potencia.

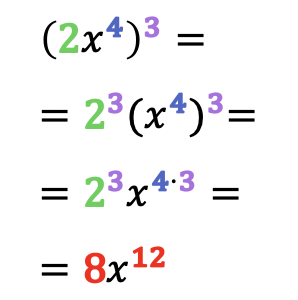
Recuerda de las propiedades de las potencias que cuando elevamos un término que ya está elevado los dos exponentes se multiplican entre sí. Por eso en la potencia de un monomio siempre se multiplica el exponente de cada letra por el exponente que indica la potencia.

Ejemplos de potencias de monomios

• 
• 
• 
• 
• 

Es bastante fácil equivocarse en este tipo de operación con monomios. Por eso te recomendamos que practiques con los ejercicios que tenemos resueltos paso a paso en nuestra web. Los encontrarás rápidamente buscándolos en el buscador de arriba a la derecha.

Valor numérico de un monomio

El valor numérico de un monomio es el resultado que se obtiene al sustituir las variables de un monomio por unos determinados valores.

Por ejemplo, si tenemos el siguiente monomio:

Si queremos hallar el valor numérico del monomio anterior para tenemos que sustituir la letra del monomio por 2 y resolver las operaciones resultantes:

De manera que el valor numérico del monomio para es igual a 20.

También se puede determinar el valor numérico de un monomio multivariable. Por ejemplo si tenemos el siguiente monomio bivariable, o dicho con otras palabras, con dos variables:

Para calcular el valor numérico del monomio anterior cuando vale 1 e vale -2, sustituimos las letras por sus respectivos valores:

Así que el valor numérico del monomio del problema para e da como resultado -6.

Monomios y polinomios

Finalmente, debes saber que a partir de los monomios se pueden hacer polinomios:

Un polinomio es la agrupación de dos o más monomios.

Por ejemplo, el polinomio anterior resulta de sumar (o restar) 3 monomios heterogéneos.

Como curiosidad, cuando un polinomio solo tiene 2 monomios se le llama binomio. Y cuando un polinomio tiene exactamente 3 monomios se dice trinomio.

Si quieres saber más sobre los polinomios puedes consultar la página principal de la web, donde explicamos todo lo que debes saber sobre los polinomios.