▷ Cómo restar monomios (ejercicios resueltos)

En este post explicamos qué es y cómo se hace la resta algebraica de monomios (semejantes o no). También podrás ver ejemplos y, además, practicar con ejercicios resueltos paso a paso de la resta de monomios.

Índice

¿Cómo se restan los monomios?

Dos o más monomios solo se pueden restar si son monomios semejantes, es decir, si ambos monomios tienen una parte literal idéntica (mismas letras y mismos exponentes).

La resta de dos monomios semejantes es igual a otro monomio compuesto por la misma parte literal y la resta de los coeficientes de esos dos monomios.

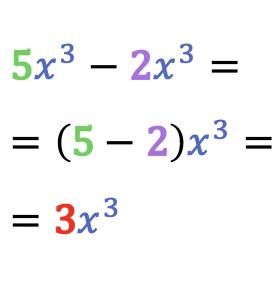
De manera que al restar un monomio menos otro monomio siempre obtendremos como resultado un monomio semejante a los dos monomios que han intervenido en la resta.

Ejemplos de restas de monomios

Te dejamos con varios ejemplos de restas entre monomios para que puedas entender del todo cómo restar dos o más monomios.

$7x^2-4x^2 = 3x^2$
$5y^3-y^3 = 4y^3$
$8x^6y-4x^6y = 4x^6y$
$10a^3b^4c^2-6a^3b^4c^2 = 4a^3b^4c^2$
$11x^3-4x^3-5x^3=7x^3-5x^3=2x^3$

En definitiva, solo se pueden restar los monomios que son semejantes. Y, en tal caso, únicamente se restan los coeficientes, a diferencia de la parte literal que queda igual.

Por lo que respecta a las propiedades de la resta de monomios, hay que tener en cuenta que la resta no cumple con las mismas propiedades de la suma. Por ejemplo, la resta de monomios no posee ni la propiedad asociativa ni la propiedad conmutativa que sí que tiene la suma de monomios.

Puedes ver las diferencias entre estos dos tipos de operaciones en la explicación de cómo sumar monomios, donde, además, encontrarás cuáles son las propiedades de la suma de monomios junto con ejemplos y ejercicios resueltos.

Resta de monomios no semejantes

Acabamos de ver que solo se pueden restar monomios semejantes. Por tanto, si nos encontramos con una resta de monomios no semejantes, es decir con el exponente diferente o con alguna variable (o letra) distinta, no podemos realizar la suma de dichos monomios de ninguna manera. Y, en ese caso, debemos dejar la operación indicada (sin resolver).

Fíjate en el siguiente ejemplo en el que restamos monomios semejantes con no semejantes:

$8x^5-2x^3-3x^5$

En la expresión algebraica anterior, el monomio $2x^3$ tiene una parte literal diferente a los otros, por lo que no lo podemos restar con los otros términos. Sin embargo, los otros dos monomios sí que se pueden restar entre sí ya que son semejantes:

$8x^5-3x^5-2x^3 = 5x^5-2x^3$

En conclusión, cuando restamos dos (o más) monomios no semejantes no los podemos agrupar y, en consecuencia, obtenemos un polinomio.

Esto es diferente cuando multiplicamos monomios, ya que se pueden multiplicar tanto monomios semejantes como monomios no semejantes. Te dejamos esta página para que puedas ver cómo se hace la multiplicación de monomios y cuáles son las diferencias de la multiplicación con la resta de monomios.

Ejercicios resueltos de la resta de monomios

Ejercicio 1

Realiza las siguientes restas de monomios:

$\text{A)} \ 6x-4x$

$\text{B)} \ -2xy^2-5xy^2$

$\text{C)} \ x^3yz-3x^3yz$

$\text{D)} \ 9a^4bc-7a^3b^2c$

Ver solución

$\text{A)} \ 6x-4x =\bm{2x}$

$\text{B)} \ -2xy^2-5xy^2= \bm{-7xy^2}$

$\text{C)} \ x^3yz-3x^3yz = \bm{-2x^3yz}$

$\text{D)} \ 9a^4bc-7a^3b^2c$

No se puede realizar la última operación de monomios porque no son semejantes (tienen distinta parte literal).

Ejercicio 2

Resuelve las siguientes restas de monomios:

$\text{A)} \ 6x^4-x^4-3x^4$

$\text{B)} \ 6abc-3abc-4abc-2abc$

$\text{C)} \ 11t^3w^2-t^3w^2-5t^3w^2-4t^3w^2$

$\text{D)} \ 9a^3b -2a^3b-4a^3b-2a^3b$

Ver solución

$\text{A)} \ 6x^4-x^4-3x^4 = \bm{2x^2}$

$\text{B)} \ 6abc-3abc-4abc-2abc= \bm{-3abc}$

$\text{C)} \ 11t^3w^2-t^3w^2-5t^3w^2-4t^3w^2 = \bm{t^3w^2}$

$\text{D)} \ 9a^3b -2a^3b-4a^3b-2a^3b = \bm{a^3b}$

Ejercicio 3

Simplifica al máximo las siguientes restas de monomios:

$\text{A)} \ 5x^7-4x^2-x^2-3x^7$

$\text{B)} \ 6x^3y^2z-4xyz-2x^3y^2z-5x^3y^2z$

$\text{C)} \ 4ab^2c -3a^2bc-5ab^2c-ab^2c$

$\text{D)} \ 15y^6-3y^3-2y^6-2y^4-7y^3-9y^6$

Ver solución

Para hacer correctamente este ejercicio hay que tener en cuenta que solo se pueden restar los monomios si son semejantes entre sí, en cambio, cuando los monomios no son semejantes no se pueden restar. Por lo tanto:

$\text{A)} \ 5x^7-4x^2-x^2-3x^7 = \bm{2x^7-5x^2}$

$\text{B)} \ 6x^3y^2z-4xyz-2x^3y^2z-5x^3y^2z = \bm{-x^3y^2z-4xyz}$

$\text{C)} \ 4ab^2c -3a^2bc-5ab^2c-a^2bc = \bm{-ab^2c-4a^2bc}$

$\text{D)} \ 15y^6-3y^3-2y^6-2y^4-7y^3-9y^6 = \bm{4y^6-2y^4-10y^3}$

¡Genial! Si has llegado hasta aquí significa que ya dominas la resta de monomios. Pero debes saber que se pueden hacer otro tipos de 👉👉operaciones con monomios👈👈 (y más difíciles), por eso te recomendamos que ahora vayas a esta página y veas cómo se calculan las otras operaciones con monomios.

¿Cómo se restan los monomios?

Ejemplos de restas de monomios

Resta de monomios no semejantes

Ejercicios resueltos de la resta de monomios

Ejercicio 1

Ejercicio 2

Ejercicio 3

Deja un comentario Cancelar respuesta