Teorema del resto (o del residuo)

Aquí encontrarás la explicación de qué es el teorema del resto (o teorema del residuo) y cómo se aplica en polinomios. También podrás ver ejemplos y, además, practicar con ejercicios resueltos paso a paso sobre el teorema del resto.

¿Qué es el teorema del resto?

En matemáticas, el teorema del resto dice que el resto de la división de un polinomio cualquiera P(x) entre otro polinomio de la forma (x-a) es igual al valor numérico del polinomio P(x) para el valor x=a, es decir, el resto de la división P(x):(x-a) es equivalente a P(a).

teorema del resto

Ejemplo del teorema del resto

Una vez hemos visto en qué consiste el teorema del resto, veamos un ejemplo práctico de su aplicación:

  • Calcula el resto de la división entre los siguientes dos polinomios:

P(x) = x^3+2x^2-4x+3 \qquad \qquad Q(x)=x-1

\cfrac{P(x)}{Q(x)}

Para hallar el resto (o residuo) de la división polinómica podemos aprovechar el teorema del resto, porque en este caso el polinomio divisor es de la forma (x-a), es decir, es de primer grado, el coeficiente de la variable x es 1 y tiene término independiente.

Así que aplicamos el teorema del resto, el cual dice que el resto de una división como esta es igual al valor numérico del polinomio dividendo evaluado en el término independiente del polinomio divisor cambiado de signo, esto es, P(1).

teorema del resto y del factor pdf

Por lo tanto, para encontrar el resto de la división tenemos que evaluar el polinomio en x=1:

\begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}

De modo que el resto de la división entre los polinomios es 2.

Por otro lado, también podemos comprobar con la regla de Ruffini para dividir polinomios que el resto coincide con el resultado que hemos encontrado:

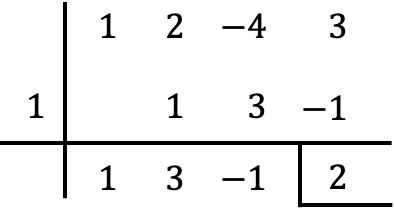
teorema del resto ruffini

Como puedes ver, es mucho más rápido y fácil determinar el resto de una división de un polinomio entre un binomio con el teorema del resto que con la regla de Ruffini, ya que se hacen muchos menos cálculos.

Teorema del resto y del factor

A partir del teorema del resto y de la definición de raíz (o cero) de un polinomio podemos deducir el teorema del factor. Así pues, el teorema del factor implica lo siguiente:

El teorema del factor dice que un polinomio P(x) es divisible por otro polinomio de la forma (x-a) si, y solo si, P(a)=0. Y, en tal caso, significa que a es una raíz o cero del polinomio P(x).

Además, según el teorema del residuo, esto quiere decir que si un polinomio es divisible por otro polinomio, el resto de dicha división es nulo, ya que P(a)=0.

Por ejemplo, si tenemos un determinado polinomio:

P(x)=x^2+2x-8

Este polinomio es divisible por el binomio (x-2) porque P(2)=0:

\begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}

Como x=2 anula el polinomio P(x), significa que x=2 es una raíz de dicho polinomio.

Y, además, como P(2)=0, podemos saber gracias al teorema del resto que el residuo de la división   \cfrac{x^2+2x-8}{x-2}   es igual a 0.

Ejercicios resueltos del teorema del resto

Para acabar de entender el teorema del resto, hemos preparado unos ejercicios resueltos paso a paso para que puedas practicar. Te aconsejamos que primero intentes hacer el ejercicio por tu cuenta y luego verifiques si lo has hecho correctamente.

Ejercicio 1

Encuentra, por el teorema del resto, el resto de la división polinomial   \cfrac{P(x)}{Q(x)}  , siendo los polinomios que intervienen en la operación:

P(x) =x^3+4x^2-2x+1\qquad \qquad Q(x)=x-2

El polinomio divisor está compuesto solamente por un término de primer grado y un término independiente y, además, el coeficiente del término de primer grado es 1. Por tanto, podemos utilizar el teorema del resto.

Y para aplicar el teorema del resto simplemente hay que evaluar el polinomio dividendo en el término independiente del polinomio divisor cambiado de signo, o dicho de otra forma, debemos calcular P(2).

\begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}

De modo que el resto de la división entre los dos polinomios es 21.

 

Ejercicio 2

Dado el polinomio P(x)=x^4-2x^3+5x^2-3x+4 , halla el resto que se obtiene al dividirlo por cada uno de los siguientes polinomios:

  • \text{A)} \ \left(x-1 \right)
  • \text{B)} \ \left(x+1 \right)
  • \text{C)} \ \left(x+2 \right)
  • \text{D)} \ \left(x-3 \right)

Como todos los polinomios divisores cumplen con las condiciones del teorema del resto, podemos usar dicho teorema para determinar el resto de cada división:

\begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}

 

\begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}

 

\begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}

 

\begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}

 

Ejercicio 3

Calcula cuánto tiene que valer el parámetro m para que el resto de la división de polinomios   \cfrac{P(x)}{Q(x)}  sea igual a 3, siendo ambos polinomios:

P(x) =x^3-5x^2-mx+9 \qquad \qquad Q(x)=x+3

En este caso particular, el polinomio que está dividiendo está formado por un monomio de primer grado y un término independiente y, a parte, el coeficiente del monomio de primer grado es 1. Por lo que podemos usar el teorema del resto.

Y para emplear el teorema del resto sencillamente hay que sustituir el término independiente del polinomio divisor cambiado de signo donde en el polinomio que es dividido haya una x, de modo que tenemos que resolver P(-3).

\begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}

Pero evidentemente obtenemos un resultado en función de la incógnita m. Sin embargo, el enunciado del problema nos dice que el resto debe ser igual a tres, por lo tanto, tenemos que igualar el resto hallado a 3:

3m-63 = 3

Y, finalmente, resolvemos la ecuación:

3m = 3+63

3m = 66

m = \cfrac{66}{3}

\bm{m = 22}

 

Ejercicio 4

Determina con el teorema del factor y del resto si el polinomio P(x) es divisible por el polinomio Q(x).

P(x) =-2x^3-5x^2-x+2 \qquad \qquad Q(x)=x+2

Para que el polinomio P(x) sea divisible por el polinomio Q(x) la división entre esos dos polinomios debe ser exacta y, por lo tanto, el resto debe ser nulo.

Entonces, como el polinomio divisor es (x+2), por el teorema del factor y el teorema del resto sabemos que el polinomio P(x) será divisible por el polinomio Q(x) si se cumple P(-2)=0. Así que debemos mirar si se verifica esta igualdad:

P(-2)=0 \quad \color{blue} \bm{?}

\begin{aligned} P(-2) &=-2\cdot (-2)^3-5\cdot (-2)^2-(-2)+2\\[2ex] &=-2 \cdot (-8) -5 \cdot 4+2 +2\\[2ex] & =16-20+2+2 \\[2ex] & =0\end{aligned}

Efectivamente, el resto de la división   \cfrac{P(x)}{Q(x)}  es igual a 0, con lo que el polinomio P(x) sí que es divisible entre el otro polinomio Q(x).

 

¿Qué te ha parecido la explicación? ¿Te ha gustado? ¡Esperemos que sí! Recuerda que puedes dejarnos cualquier sugerencia o cualquier duda que tengas en los comentarios. ⬇⬇⬇ ¡Os leemos a todos! 😁😁

10 comentarios en “Teorema del resto (o del residuo)”

  1. jose aranguren

    Excelente muchachos, buen trabajo, se aclaran muchas dudas con respecto al resto y se simplifica mucho el trabajo, no se si le podrían agregar algo sobre las soluciones de los polinomios al igualarlos a cero y su relacion con los coeficientes

    Responder
    1. Polinomios

      ¡Muchas gracias por tu comentario Jose! 🙂
      Puedes añadir toda la información que quieras en los comentarios, ¡todas las colaboraciones son más que bienvenidas! 👍

  2. Julio Bravo B.

    Caramba que buen trabajo sobre los conocimientos de factorización y cálculo de las raíces de un polinomio, felcitaciones, pude refrescar extrordinariamente todos esos procedimientos y traerlos a flote así contribuiré con la formación familiares y vecinos. Gracias muchas gracias

    Responder
  3. Emyyy

    Buena explicación y la distribución de los problemas, me encanta, pude practicar fácilmente con este sitio web. Buen trabajo 🙂

    Responder
  4. Guembe, M Reyes

    S0y una persona mayor que intenta ayudar a unas hermanas con situación familiar desastrosa, así que agradezco que me ofrezcan ayuda (no cobro nada, más bien lo contrario), por lo que le doy las gracias. Me ha servido de mucha ayuda, yo hice Bachiller de «Letras», gracias a un profe de Mates horroroso como profesor y como persona, pero hasta entonces a mi las mates me habían gustado, pero me quedé en las ecuaciones de 1º y 2º grado, en 4º de bachillerato.

    Responder
    1. Polinomios

      ¡Me alegro de conocer vuestra historia! Nunca es tarde para aprender matemáticas.

      Muchas gracias por tu comentario y espero que te resulte útil esta página web. ¡Cualquier duda que te surja puedas preguntarla en los comentarios!

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio