▷ Cómo sacar (o extraer) factor común ✅ (ejercicios resueltos)

En esta página explicamos cómo sacar (o extraer) factor común de un polinomio. Aquí encontrarás los distintos tipos de factor común y podrás ver varios ejemplos de cómo se hace. Además, podrás practicar con ejercicios resueltos paso a paso.

Índice

¿Qué es el factor común?

En matemáticas, el factor común es un factor que está presente en todos los términos de un polinomio, es decir, el factor común consiste en un número o una letra que multiplica a cada término de un polinomio.

A modo de ejemplo, vamos a identificar cuál es el factor común del siguiente polinomio:

$4x+4y$

En número 4 se repite en todos los términos del polinomio:

$\color{red} \bm{4} \color{black} x + \color{red} \bm{4} \color{black} y$

Por lo tanto, el factor en común de este polinomio es igual a 4.

$\displaystyle \text{Factor com\'un} = 4 {\phantom{\frac{1}{2}}$

Cómo sacar (o extraer) factor común

Una vez ya sabemos el significado de factor común, vamos a ver cómo se saca factor común de un polinomio.

Cuando dos o más términos de un polinomio tienen un factor común, se puede sacar (o extraer) factor común para transformar las sumas o restas del polinomio en una multiplicación.

Puede que escrito te parezca un poco difícil, así que mejor veamos cómo se extrae factor común de un polinomio con un ejemplo:

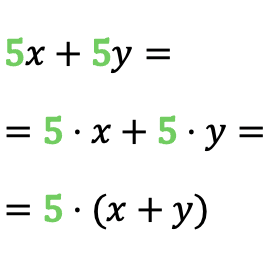
extraer o sacar factor comun de un polinomio

Como puedes ver en el ejemplo, el número 5 está repetido en el monomio 5x y en el monomio 5y, por lo tanto, el factor común del polinomio es 5. Entonces, una vez hemos identificado el factor común podemos convertir la suma de monomios en un producto.

No te olvides de poner el paréntesis al hacer la extracción del factor común, ya que el factor común debe multiplicar a todos los sumandos.

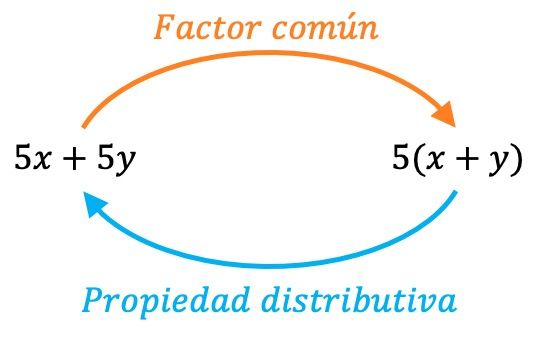
Sacar factor común es la operación inversa de la propiedad distributiva, es decir, en realidad estamos aplicando la propiedad distributiva al revés. Por lo tanto, siempre podemos verificar que hemos extraído factor común de manera correcta haciendo el proceso inverso:

Si al aplicar la propiedad distributiva obtenemos el mismo polinomio del principio, significa que hemos sacado factor común de manera correcta.
En cambio, cuando el resultado de emplear la propiedad distributiva es otro polinomio diferente al polinomio original, implica que hemos cometido algún error en el proceso de extraer factor común.

Ejemplos de sacar (o extraer) factor común

Te dejamos con más ejemplos para acabar de entender el concepto del factor común:

Ejemplo 1

Como ves en este ejemplo, se puede extraer factor común a más de dos términos a la vez:

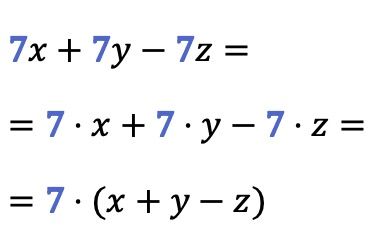
Ejemplo 2

También se puede sacar factor común de las variables (o letras):

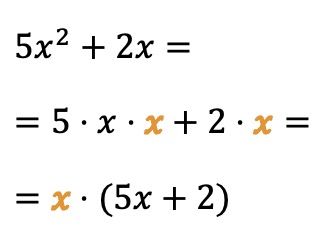
extraer factor comun en expresiones algebraicas

En este caso la letra x está multiplicando a los dos términos del polinomio, así que podemos simplificar la expresión algebraica sacando como factor común la variable x.

Ejemplo 3

En este ejemplo el primer término tiene la variable x elevada a 3 y en el segundo término la x está elevada a la 2, de manera que ambos términos tienen dos x. Por lo tanto, el factor común no es solamente una x, sino x²:

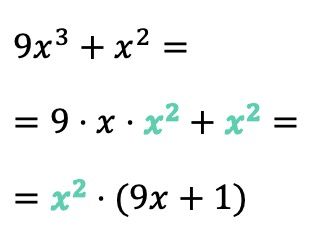
Por otro lado, fíjate que si el factor común del polinomio coincide exactamente con un término, cuando extraemos el factor común debemos poner un 1 en su lugar. De lo contrario, si no pusiésemos nada en su lugar, no obtendríamos una expresión equivalente.

Ejemplo 4

A veces, el factor común no es tan evidente y no se ve directamente, sino que se trata de un divisor de los coeficientes de los monomios. Por ejemplo, el factor común del siguiente ejemplo es 3, ya que la descomposición factorial tanto del 6 como del 9 contiene el 3:

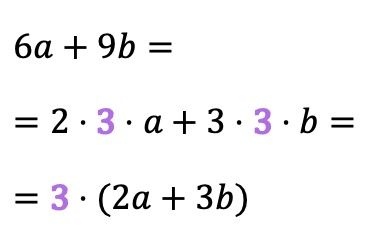
A este tipo de factor común se le llama en algunos libros de álgebra máximo factor común, ya que el factor común es a la vez el máximo común divisor (MCD) de los coeficientes de los términos del polinomio.

Si has llegado hasta aquí quiere decir que seguramente ya sabes cómo encontrar el factor común de un polinomio, perfecto. Sin embargo, ¿no te has preguntado para qué sirve el factor común? Pues una aplicación del factor común es que se usa para factorizar polinomios. Si aún no sabes qué es, en este enlace puedes ver en qué consiste la factorización de polinomios y por qué el factor común es tan importante para hacer esta operación polinómica.

Factor común en fracciones

El factor común también resulta muy útil para simplificar términos en fracciones con polinomios en el numerador y en el denominador.

Para ver cómo se hace, vamos a simplificar a modo de ejemplo la siguiente fracción:

$\cfrac{2x^2+4}{14x+8y}$

Lo primero que debemos hacer es hallar el factor común del polinomio del numerador y del polinomio del denominador. En este caso, el factor común de ambos polinomios es 2:

$\cfrac{\color{red} \bm{2} \color{black}\cdot x^2+\color{red} \bm{2} \color{black}\cdot 2 }{\color{red} \bm{2} \color{black}\cdot 7x+\color{red} \bm{2} \color{black} \cdot 4y}$

Ahora extraemos factor común de los dos polinomios:

$\cfrac{\color{red} \bm{2} \color{black}\left(x^2+2\right)}{\color{red} \bm{2} \color{black}\left(7x+4y\right)}$

Y una vez hemos sacado factor común en los dos polinomios, tenemos que quitar los factores que se repiten en el numerador y en el denominador:

$\cfrac{\cancel{2}\left(x^2+2\right)}{ \cancel{2}\left(7x+4y\right)}$

En conclusión, la fracción simplificada queda:

$\cfrac{x^2+2}{7x+4y}$

Factor común por agrupación

Una manera de reducir los términos que tiene un polinomio es mediante el método de factor común por agrupación de términos, también llamado doble extracción de factor común. Tal y como indica su nombre, este procedimiento se basa en simplificar la expresión de un polinomio agrupando sus términos dos veces.

Este método es un poco complejo, por lo que vamos a ver cómo se aplica paso a paso con el siguiente polinomio:

$x^2+2x+5x+10$

Primero debemos determinar dos posibles factores comunes diferentes, por lo que separamos el polinomio en dos partes:

$(x^2+2x)+(5x+10)$

En este caso los elementos x² y 2x tienen de factor común la letra x, y los términos 5x y 10 tienen como factor común el 5 (ya que 10 es un múltiplo de 5). De modo que sacamos estos dos factores en común:

$(x\cdot x+2\cdot x)+(5\cdot x+5\cdot 2)$

$x(x+2)+5(x+2)$

Y, por último, como los dos productos polinómicos restantes tienen el factor (x+2), podemos simplificar el polinomio de la siguiente manera:

$(x+2)\cdot (x+5)$

Como puedes comprobar, este método no es nada fácil. Así que no dudes en preguntarnos cualquier duda que te surja en los comentarios, que la responderemos lo antes posible.

Ejercicios resueltos paso a paso de factor común

Te dejamos con varios ejercicios resueltos paso a paso para que puedas practicar cómo extraer factor común a un polinomio.

Ejercicio 1

Extrae factor común de los siguientes polinomios:

$\text{A)} \ 6a+6b$

$\text{B)} \ 3x^2+8x$

$\text{C)} \ 2x-4$

$\text{D)} \ -5x^4+x^2$

Ver solución

A) Todos los términos que componen el primer polinomio tienen un 6, con lo que el factor común del polinomio es 6:

$6a+6b = 6\cdot a + 6 \cdot b = \bm{6\cdot (a+b)}$

B) En el segundo polinomio todos sus elementos tienen, como mínimo, una letra x. Por tanto, ese es el factor común del polinomio:

$3x^2+8x = 3x \cdot x+8\cdot x= \bm{x\cdot (3x+8)}$

C) El primer monomio del polinomio tiene, evidentemente, un 2, y el segundo monomio es un múltiplo de 2. Así que el factor común del polinomio es 2:

$2x-4= 2\cdot x - 2\cdot 2 =\bm{2\cdot (x-2)}$

D) En el último polinomio todas las variables están elevadas, como mínimo, al cuadrado. De modo que el factor común es x²:

$-5x^4+x^2= -5x^2\cdot x^2 +1 \cdot x^2 = \bm{x^2\cdot (-5x^2+1)}$

Recuerda que cuando el factor en común es idéntico a un término se debe poner un 1 en su lugar.

Ejercicio 2

Saca factor común de los siguientes polinomios:

$\text{A)} \ 8x^2 + 10y^3$

$\text{B)} \ 5x^3-2x^2+4x$

$\text{C)} \ 25x^5+15x^3-20$

$\text{D)} \ 9x^4-3x^3-21x^2-6x$

Ver solución

A) Todos los coeficientes de los elementos que forman el primer polinomio son múltiplos de 2, en consecuencia, al extraer factor común el polinomio queda:

$\begin{array}{l} 8x^2 + 10y^3 = \\[2ex] = 2\cdot 4x^2 +2\cdot 5y^3 = \\[2ex] = \bm{2\left(4x^2+5y^3\right)} \end{array}$

B) En todos los términos del polinomio hay, como mínimo, una x, por tanto:

$\begin{array}{l}5x^3-2x^2+4x = \\[2ex] = 5x^2\cdot x-2x\cdot x+4\cdot x= \\[2ex] =\bm{x\left(5x^2-2x+4\right)}\end{array}$

C) El máximo común divisor de los coeficientes de todos los términos del polinomio es 5, de forma que el factor común de dicho polinomio es 5:

$\begin{array}{l}25x^5+15x^3-20 = \\[2ex] =5\cdot 5x^5+5\cdot 3x^3-5\cdot 4 = \\[2ex] = \bm{5\left(5x^5+3x^3-4\right)}\end{array}$

D) Todos los términos del polinomio tienen al menos una x, y, además, todos los coeficientes son múltiples de 3. Por lo tanto, el factor común del polinomio es 3x:

$\begin{array}{l}9x^4-3x^3-21x^2-6x = \\[2ex] = 3x^3\cdot 3x-x^2\cdot 3x-7x\cdot 3x-2\cdot 3x= \\[2ex] = \bm{3x\left(3x^3-x^2-7x-2 \right)}\end{array}$

Ejercicio 3

Encuentra el factor común de cada uno de los siguientes polinomios y sácalo:

$\text{A)} \ 4a^2b^5+7a^4b^3-10a^6b^4$

$\text{B)} \ 16x^4y^7z+8x^2y^2z^2+ 24x^3y^5$

$\text{C)} \ 6ab^2c^4-6ab^2c+12a^3b^2c$

$\text{D)} \ 18x^2y+10xy-5xy^3+4z$

Ver solución

A) Todos los monomios tienen por lo menos la letra $a$ elevada al cuadrado y la letra $b$ elevada al cubo, por tanto, el factor común es $a^2b^3:$

$\begin{array}{l} 4a^2b^5+7a^4b^3-10a^6b^4 = \\[2ex] = 4b^2\cdot a^2b^3+7a^2\cdot a^2b^3-10a^4b\cdot a^2b^3 = \\[2ex] = \bm{a^2b^3\left(4b^2+7a^2-10a^4b\right)} \end{array}$

B) Todos los coeficientes del polinomio son múltiplos de 8 y, además, tienen mínimamente como parte literal x² y y². De forma que el factor común del polinomio es 8x²y².

$\begin{array}{l}16x^4y^7z+8x^2y^2z^2+ 24x^3y^5 = \\[2ex] = 2x^2y^5z \cdot 8x^2y^2 +z^2\cdot 8x^2y^2+ 3xy^3\cdot 8x^2y^2= \\[2ex] =\bm{8x^2y^2\left(2x^2y^5z+z^2+3xy^3\right)}\end{array}$

C) En este caso el factor común coincide con el valor del monomio intermedio $\left(6ab^2c\right)$ , ya que los coeficientes de los otros monomios son múltiples de $6$ y absolutamente todos poseen $ab^2c:$

$\begin{array}{l}6ab^2c^4-6ab^2c+12a^3b^2c = \\[2ex] =c^3\cdot 6ab^2c -1\cdot 6ab^2c+2a^2 \cdot 6ab^2c = \\[2ex] = \bm{6ab^2c\left(c^3-1+2a^2\right)}\end{array}$

D) En este caso particular, el polinomio no tiene factor común, ya que ningún factor se repite en todos los términos del polinomio. En consecuencia, no se puede simplificar algebraicamente la expresión del polinomio.

$18x^2y+10xy-5xy^3+4z$

Ejercicio 4

Simplifica las siguientes fracciones algebraicas sacando factor común:

$\text{A)} \ \cfrac{10x^2+30}{5x-20}$

$\text{B)} \ \cfrac{16x^2-8}{24x-32}$

$\text{C)} \ \cfrac{49x^3+7x}{35x^2-14}$

$\text{D)} \ \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}$

Ver solución

El procedimiento para simplificar una fracción algebraica, es decir una fracción con polinomios, consiste en extraer factor común del numerador y del denominador de la fracción, y luego eliminar los factores que se repiten arriba y abajo de la fracción. Por lo tanto:

$\text{A)} \quad \begin{array}{l} \cfrac{10x^2+30}{5x-20}= \cfrac{5\cdot 2x^2 +5\cdot 6}{5\cdot x-5\cdot 4} = \\[4ex] = \cfrac{5(2x^2+6)}{5(x-4)}= \cfrac{\cancel{5}(2x^2+6)}{\cancel{5}(x-4)} = \\[4ex] = \cfrac{\bm{2x^2+6}}{\bm{x-4}} \end{array}$

$\text{B)} \quad \begin{array}{l} \cfrac{16x^2-8}{24x-32} = \cfrac{8 \cdot 2x^2+8 \cdot (-1)}{8 \cdot 3x-8 \cdot 4} =\\[4ex] = \cfrac{8(2x^2-1)}{8(3x-4)}= \cfrac{\cancel{8}(2x^2-1)}{\cancel{8}(3x-4)} =\\[4ex] = \cfrac{\bm{2x^2-1}}{\bm{3x-4}} \end{array}$

$\text{C)} \quad \begin{array}{l}\cfrac{49x^3+7x}{35x^2-14}=\cfrac{7x\cdot 7x^2+7x\cdot 1}{7 \cdot 5x^2+7\cdot (-2)} =\\[4ex] = \cfrac{7x(7x^2+1)}{7(5x^2-2)}= \cfrac{\cancel{7}x(7x^2+1)}{\cancel{7}(5x^2-2)}=\\[4ex] = \cfrac{\bm{x(7x^2+1)}}{\bm{5x^2-2}} \end{array}$

$\text{D)} \quad \begin{array}{l} \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}=\cfrac{4x^2\cdot 2x^2+4x^2\cdot 4x+4x^2\cdot (-1)}{4x\cdot 3x+4x\cdot 5}=\\[4ex] = \cfrac{4x^2(2x^2+4x-1)}{4x(3x+5)}= \cfrac{\cancel{4}x^{\cancel{2}}(2x^2+4x-1)}{\cancel{4}\cancel{x}(3x+5)}=\\[4ex] = \cfrac{\bm{x(2x^2+4x-1)}}{\bm{3x+5}} \end{array}$

Ejercicio 5

Saca factor común a las siguientes expresiones polinómicas:

$\text{A)} \ \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}$

$\text{B)} \ \sqrt{12x^3+16}$

$\text{C)} \ x^2+4x-3x-12$

$\text{D)} \ \cfrac{3}{4}x^2+ \cfrac{1}{2}x-\cfrac{5}{6}$

Ver solución

A) Todos los términos del polinomio se pueden descomponer factorialmente con un tercio, por tanto:

$\begin{array}{l} \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}= \\[3ex] = \cfrac{1}{3}\cdot 7x^2+ \cfrac{1}{3}\cdot 8x-\cfrac{1}{3}\cdot 2 = \\[3ex] = \mathbf{\cfrac{1}{3}}\bm{\left(7x^2+8x-2\right)} \end{array}$

B) El factor común de polinomio de dentro de la raíz es 4 pero, entonces, podemos sacar el factor común fuera calculando su raíz cuadrada:

$\begin{array}{l}\sqrt{12x^3+16}= \\[2ex] =\sqrt{4\cdot 3x^3+4\cdot 4}= \\[2ex]=\sqrt{4\left(3x^3+4\right)}= \\[2ex] =\bm{2\sqrt{3x^3+4}}\end{array}$

C) En este polinomio podemos aplicar el proceso de extraer factor común por agrupación:

$\begin{array}{l}x^2+4x-3x-12= \\[2ex] =x(x+4)-3(x+4) = \\[2ex] = \bm{(x+4)(x-3)}\end{array}$

D) Todos los coeficientes fraccionarios del polinomio son múltiples de un medio, por lo que el factor común del polinomio es ½.

$\begin{array}{l}\displaystyle \frac{3}{4}x^2+ \frac{1}{2}x-\frac{5}{6}= \\[4ex] \displaystyle = \frac{1}{2}\cdot\frac{3}{2}x^2+ \frac{1}{2}\cdot x-\frac{1}{2}\cdot\frac{5}{3}= \\[4ex] \displaystyle = \mathbf{\frac{1}{2}}\bm{\left(}\mathbf{\frac{3}{2}}\bm{x^2+x-}\mathbf{\frac{5}{3}} \bm{\right)}\end{array}$

👇👇👇 ¿Qué te ha parecido la explicación? ¿Te ha gustado? Recuerda también que si tienes alguna duda de cómo se determina el factor común de un polinomio o no entiendes algún ejercicio siempre puedes preguntarnos en los comentarios, que te contestaremos. 👇👇👇

4 comentarios en “Extraer o sacar factor común”

TIBERI
16/07/2021 a las 23:37

Excelente

Responder
1. Polinomios
  18/07/2021 a las 19:25
  
  ¡Muchas gracias!
Narcisa Ortiz
08/04/2023 a las 01:00

Gracias ,por el excelente material

Responder
1. Polinomios
  11/04/2023 a las 22:06
  
  ¡Gracias Narcisa!

¿Qué es el factor común?

Cómo sacar (o extraer) factor común

Ejemplos de sacar (o extraer) factor común

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4

Factor común en fracciones

Factor común por agrupación

Ejercicios resueltos paso a paso de factor común

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

4 comentarios en “Extraer o sacar factor común”

Deja un comentario Cancelar respuesta