Suma de polinomios

En esta página encontrarás la explicación de cómo se hace la suma de polinomios. Además, podrás ver ejemplos de sumas de polinomios e incluso ejercicios resueltos paso a paso. Finalmente, también explicamos cuáles son las propiedades de este tipo de operación con polinomios.

¿Cómo se hace la suma de polinomios?

En matemáticas, para hacer la suma de dos o más polinomios se deben sumar los términos de los polinomios que son semejantes. Es decir, la suma de polinomios consiste en sumar los términos que tienen la misma parte literal (mismas variables y mismos exponentes).

Así pues, una suma de polinomios se puede realizar de dos formas distintas: con el método vertical o con el método horizontal. A continuación tienes la explicación de ambos procedimientos, pero te aconsejamos que primero aprendas cómo sumar polinomios de manera vertical y luego pases al método horizontal. Aunque evidentemente quédate con el que tú prefieras.

Suma de polinomios vertical

A continuación vamos a ver cómo se suman dos polinomios de manera vertical mediante un ejemplo:

• Realiza la suma de los siguientes dos polinomios:

Lo primero que debemos hacer es colocar un polinomio debajo de otro, de manera que los términos semejantes de los dos polinomios estén alineados por columnas:

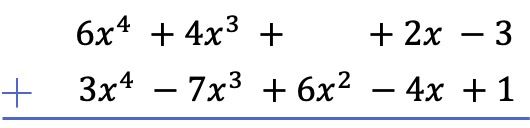
Atención: Si un polinomio no tiene término de un determinado grado, debemos dejar el espacio en blanco. Por ejemplo no tiene monomio de grado 2, por eso hay un espacio en blanco en su sitio.

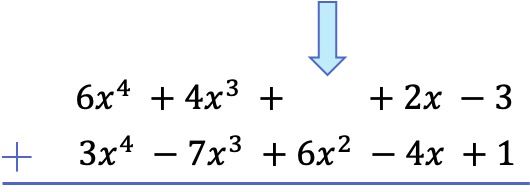
Una vez hemos puesto todos los términos por orden de mayor a menor grado, sumamos los coeficientes de cada columna manteniendo las partes literales iguales:

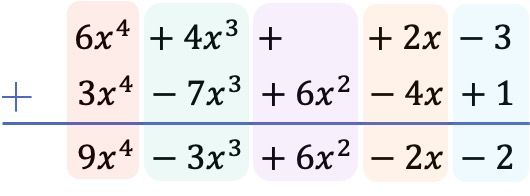
Por lo tanto, el resultado obtenido de la suma de los 2 polinomios es:

Ahora que ya entiendes la suma de polinomios, debes saber que también se pueden hacer sumas de fracciones formadas por polinomios. A este tipo de operación se le llama suma de fracciones algebraicas. Haz click en este enlace y descubre no solo cómo se calculan las sumas de fracciones algebraicas, sino también cómo se resuelven todas las operaciones con fracciones algebraicas.

Suma de polinomios horizontal

Acabamos de ver cómo se suman los polinomios verticalmente, pero ahora vamos a ver el otro método que hay para hacer una suma de polinomios: sumar polinomios horizontalmente. Seguramente este procedimiento es más rápido que el anterior, sin embargo es necesario tener más dominio de los conceptos de los polinomios.

Así pues, veamos en qué consiste este método de sumar polinomios mediante un ejemplo. Y para que puedas ver las diferencias entre los dos métodos, sumaremos los mismos polinomios que en el ejemplo anterior:

• Calcula la suma de los siguientes dos polinomios:

En primer lugar, tenemos que posicionar los dos polinomios en una misma operación, o dicho con otras palabras, uno detrás del otro:

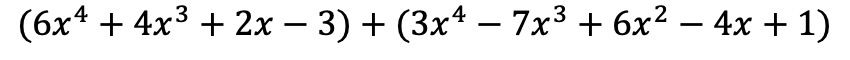
Y ahora sumamos los términos que tienen partes literales idénticas, es decir, los términos con las mismas variables (letras) y los mismos exponentes. Los términos que no son semejantes no se pueden sumar.

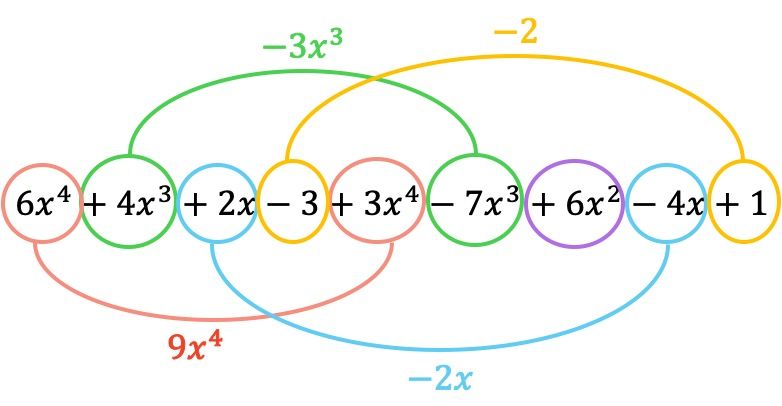
De modo que el polinomio resultante de la suma es:

Como puedes comprobar, hemos obtenido el mismo resultado con los dos métodos, así que cuando hagas una adición de polinomios puedes usar el que te vaya mejor.

Ejercicios resueltos de la suma de polinomios

Para que puedas practicar, te dejamos con varios ejercicios resueltos de sumas de polinomios. Si tienes alguna duda, puedes preguntarla en los comentarios de la página y la contestaremos lo antes posible.

Ejercicio 1

Suma los siguientes dos polinomios:

En este caso, sumaremos los dos polinomios de manera vertical. Para ello, ordenamos los polinomios por grado y sumamos los monomios situados en la misma columna:

 

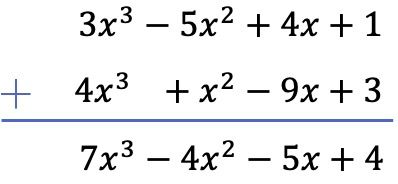
Ejercicio 2

Resuelve la suma de los siguientes dos polinomios:

Haremos la suma de los dos polinomios utilizando el método vertical. De modo que ordenamos los polinomios por grado y sumamos los términos situados en la misma columna:

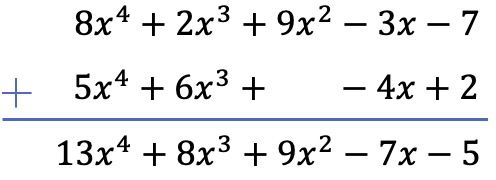
Fíjate que en este caso particular se debe dejar un espacio vacío en la columna de grado 2 del segundo polinomio, porque no tiene término de segundo grado.

 

Ejercicio 3

¿Cuánto vale la suma de los siguientes dos polinomios?

Realizaremos la adición de los dos polinomios utilizando el método vertical. Por lo tanto:

 

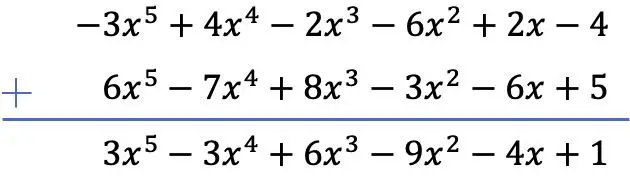
Ejercicio 4

Calcula la suma de los siguientes tres polinomios:

Calcularemos la suma de los 3 polinomios utilizando el método vertical. De modo ponemos los polinomios ordenados por grado y sumamos los términos situados en la misma columna:

 

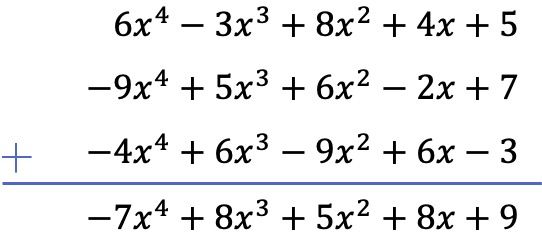
👉👉👉Ahora que ya has visto cómo se suman dos polinomios, puede que te interese otra operación característica de los polinomios: el factor común. Extraer factor común de un polinomio es bastante complicado (y difícil de entender), de hecho, se suelen cometer muchos fallos haciendo esta operación. Por eso hemos elaborado una guía donde explicamos cómo extraer factor común paso a paso, para que lo entiendas perfectamente y no te equivoques al hacer esta operación. Descubre cuáles son los trucos para extraer bien factor común de un polinomio haciendo click en el enlace.

Propiedades de la suma de polinomios

La suma de polinomios cumple con las siguientes características:

• Propiedad asociativa: cuando se suman 3 o más polinomios no importa cómo se agrupen los polinomios, ya que el resultado siempre es el mismo. Es decir, se cumple la siguiente igualdad:

• Propiedad conmutativa: en la suma de polinomios el orden de los sumandos no altera el resultado de la suma.

• Elemento neutro: evidentemente, sumar un polinomio más cualquier otro polinomio de valor numérico cero es equivalente al primer polinomio.

• Elemento opuesto: el resultado de sumar cualquier polinomio más su polinomio opuesto siempre es nulo.

¿Qué te ha parecido la explicación? ¿Te ha sido útil? ¿Con qué método para sumar polinomios te quedas tú, el vertical o el horizontal? ¡Os leemos en los comentarios! 👀