Cómo calcular la potencia de un monomio (ejemplos y ejercicios)

Aquí encontrarás la explicación de cómo calcular la potencia de un monomio. Además, podrás ver varios ejemplos de potencias de monomios e incluso practicar con ejercicios resueltos paso a paso.

Índice

¿Cuál es la potencia de un monomio?

En matemáticas, para calcular la potencia de un monomio se eleva cada elemento del monomio al exponente de la potencia. Es decir, la potencia de un monomio consiste en elevar su coeficiente y sus variables (letras) al exponente de la potencia.

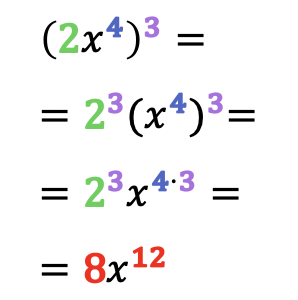
Recuerda de las propiedades de las potencias que cuando elevamos un término que ya está elevado los dos exponentes se multiplican entre sí. Por eso en la potencia de un monomio siempre se multiplica el exponente de cada letra por el exponente que indica la potencia.

Por otro lado, también hay que tener en cuenta que el resultado de la potencia de un monomio depende del signo del monomio:

La potencia de un monomio positivo siempre da lugar a otro monomio positivo, independientemente de la paridad del exponente:

$\left(3x^5\right)^2 = 3^2\left(x^5\right)^2 = 9x^{10}$

$\left(3x^5\right)^3 = 3^3\left(x^5\right)^3 = 27x^{15}$

Un monomio negativo elevado a una potencia con exponente par da como resultado un monomio positivo:

$\left(-3x^5\right)^2 = (-3)^2\left(x^5\right)^2 = 9x^{10}$

Un monomio negativo elevado a una potencia con exponente impar siempre es igual a otro monomio negativo:

$\left(-3x^5\right)^3 = (-3)^3\left(x^5\right)^3 = -27x^{15}$

Ejemplos de potencias de monomios

Para que puedas entender del todo cómo se calcula la potencia de un monomio, a continuación te dejamos con varios ejemplos de la potenciación de monomios:

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

Como puedes ver, hallar la potencia de un monomio es relativamente fácil. Sin embargo, hay algunas operaciones con monomios que son más complicadas como por ejemplo la multiplicación y la división. Es por eso que te recomendamos que le eches un vistazo a las siguientes páginas donde se explica cómo multiplicar monomios y cómo dividir monomios.

Ejercicios resueltos de la potencia de un monomio

A continuación tienes varios ejercicios resueltos paso a paso de potencias de monomios para que puedas practicar más:

Ejercicio 1

Calcula las siguientes potencias de monomios:

$\text{A)} \ \left(-8x^4\right)^2$

$\text{B)} \ \left(2x^5\right)^4$

$\text{C)} \ \left(-2a^7\right)^3$

$\text{D)} \ \left(7x^3\right)^3$

Ver solución

$\text{A)} \ \left(-8x^4\right)^2=(-8)^2\left(x^4\right)^2 = (-8)^2x^{4\cdot 2} = \bm{64x^{8}}$

$\text{B)} \ \left(2x^5\right)^4=2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = \bm{16x^{20}}$

$\text{C)} \ \left(-2a^7\right)^3=(-2)^3\left(a^7\right)^3 = (-2)^3a^{7\cdot 3} = \bm{-8a^{21}}$

$\text{D)} \ \left(7x^3\right)^3 =7^3\left(x^3\right)^3 = 7^3x^{3\cdot 3} = \bm{343x^{9}}$

Ejercicio 2

Resuelve las siguientes potencias de monomios:

$\text{A)} \ \left(5x^8y^2\right)^3$

$\text{B)} \ \left(-x^3y^5z^4\right)^6$

$\text{C)} \ \left(-3x^3yz\right)^3$

$\text{D)} \ \left(-2x^5y^4\right)^5$

Ver solución

$\text{A)} \ \left(5x^8y^2\right)^3=(5)^3\left(x^8y^2\right)^3 = \bm{125x^{24}y^6}$

$\text{B)} \ \left(-x^3y^5z^4\right)^6=(-1)^6\left(x^3y^5z^4\right)^6 = \bm{x^{18}y^{30}z^{24}}$

$\text{C)} \ \left(-3x^3yz\right)^3=(-3)^3\left(x^3yz\right)^3 = \bm{-27x^9y^3z^3}$

$\text{D)} \ \left(-2x^5y^4\right)^5 =(-2)^5\left(x^5y^4\right)^5 = \bm{-32x^{25}y^{20}}$

Si has llegado hasta aquí significa que ya sabes resolver ejercicios de potencias de monomios. ¡Perfecto!👍 El siguiente paso es aprender a calcular operaciones combinadas con monomios (más de una operación a la vez). ¡Así que es hora de pasar al siguiente nivel e intentar hacer estos 👉👉ejercicios resueltos de operaciones con monomios!👈👈

6 comentarios en “Potencia de un monomio”

Nayelis
27/08/2021 a las 00:49

Resuelve las siguientes potencias de monomios
A). (B²)³
B).((m³)³)⁴
C).(2m²)³
D).(4b³)²
E).(-6)³)⁴

Responder
1. Polinomios
  27/08/2021 a las 11:01
  
  Hola Nayelis, resolvemos las potencias de los monomios a continuación:
  
  $\text{A) }= \left(B^2\right)^3=B^6$
  
  $\text{B) }= \left(\left(m^3\right)^3\right)^4=m^{3\cdot 3\cdot 4}=m^{36}$
  
  $\text{C) }= \left(2m^2\right)^3=8m^6$
  
  $\text{D) }= \left(4b^3\right)^2=16b^6$
  
  $\text{E) }= \left(\left(-6\right)^3\right)^4=(-6)^{12}=6^{12}$
2. Alisson
  15/10/2021 a las 18:18
  
  (-4rs)³=
  (5pq)²=
  (-2a)⁴=
  (-5×)²=
  (10yz)³=
3. Polinomios
  20/10/2021 a las 14:02
  
  Hola Alisson, tienes las potencias de los monomios resueltas a continuación:
  
  $(-4rs)^3=-64r^3s^3$
  
  $(5pq)^2=25p^2q^2$
  
  $(-2a)^4)=16a^4$
  
  $(-5x)^2=25x^2$
  
  $(10yz)^3=1000y^3z^3$
Angieo
29/08/2021 a las 03:51

(2x²)⁴ ×(2x²)³ ×2x²
(3x²)⁴ ×(3x⁴ +x¹⁴)

Responder
1. Polinomios
  31/08/2021 a las 10:20
  
  Hola Angieo, tienes los ejercicios que has propuesto resueltos a continuación:
  
  $\left(2x^2\right)^4\cdot \left(2x^2\right)^3\cdot 2x^2= 16x^8\cdot 8x^6\cdot 2x^2=256x^{16}$
  
  $\left(3x^2\right)^4\cdot \left(3x^4+x^{14}\right)=81x^8\cdot 3x^4+81x^8\cdot x^{14}=243x^{12}+81x^{22}$