▷ Cómo resolver el cuadrado de una diferencia (fórmula y ejemplos)

Aquí explicamos cuál es la fórmula de la identidad notable del cuadrado de una diferencia (o resta), es decir, te enseñamos cómo se resuelve la expresión (a-b)². Además, podrás ver ejemplos y practicar con ejercicios resueltos sobre el cuadrado de una diferencia. Y, finalmente, mostramos la demostración de la fórmula y la interpretación geométrica de este tipo de producto notable.

Índice

¿Qué es el cuadrado de una diferencia (o resta)?

El cuadrado de una diferencia, o cuadrado de una resta, es una de las identidades notables (o productos notables), es decir, consiste en una regla matemática que facilita el cálculo de elevar al cuadrado un binomio con dos términos: uno positivo y otro negativo.

Por lo tanto, la expresión algebraica del cuadrado de una diferencia es (a-b)².

Fórmula del cuadrado de una diferencia (o resta)

Una vez hemos visto la definición del este tipo de identidad notable, vamos a ver cómo resolver el cuadrado de una diferencia con su fórmula:

formula del cuadrado de una diferencia o resta

De modo que el cuadrado de una diferencia es igual al cuadrado del primer término, menos el doble del producto del primero por el segundo, más el cuadrado del segundo.

Por lo tanto, para calcular una diferencia o una resta al cuadrado no solo hay que elevar cada término a la dos, sino que, además, se deben multiplicar entre sí y por 2.

Es importante recordar esto, ya que un error muy común al hacer cuadrados de restas es no poner el producto entre los dos términos y resolver solamente el cuadrado del minuendo y del sustraendo de la resta:

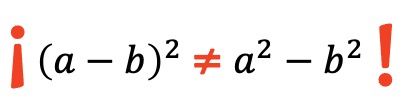
¡No te olvides del producto entre a y b!

Ejemplos de cuadrados de diferencias (o restas)

Ahora que ya sabemos cuál es la fórmula del cuadrado de una diferencia, ya podemos hacer cálculos con ella. Y para que puedas ver cómo se hace, te hemos preparado varios ejemplos resueltos del cuadrado de una diferencia (o resta).

Ejemplo 1

Resuelve la siguiente diferencia elevada al cuadrado:

$(x-3)^2$

Se trata de una resta al cuadrado, por lo tanto, tenemos que aplicar su fórmula:

$(a-b)^2=a^2-2ab+b^2$

Entonces, tenemos que identificar cuáles son los valores de las incógnitas $a$ y $b$ de la fórmula. En este caso, $a$ es la variable $x$ y $b$ corresponde al número 3:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}$

Fíjate que el signo negativo no forma parte de $b,$ sino que siempre tenemos que coger el número sin el signo para aplicar la fórmula correctamente.

De modo que ya sabemos los valores de $a$ y de $b$ , por tanto, tan solo tenemos que sustituir dichos valores en la fórmula:

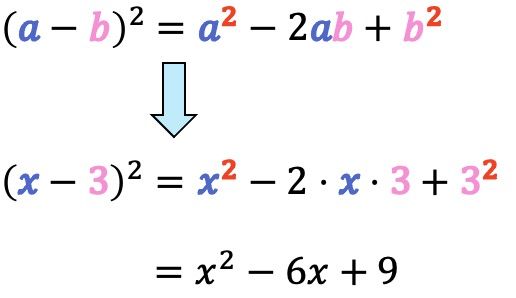
binomio de una resta al cuadrado ejercicios resueltos

Ejemplo 2

Calcula el siguiente binomio de una resta elevado al cuadrado:

$(5x-2)^2$

La fórmula de la diferencia al cuadrado es:

$(a-b)^2=a^2-2ab+b^2$

Así pues, primero tenemos que identificar los valores de $a$ y de $b$ de la fórmula. En este problema, $a$ representa el monomio $5x$ y $b$ es equivalente al término independiente del binomio, esto es, 2:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (5x-2)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=5x \\[2ex] b=2 \end{array}$

Finalmente, una vez conocemos el valor de los parámetros $a$ y $b$ , simplemente aplicamos la fórmula del binomio de un resta elevado al cuadrado:

$\begin{aligned} (5x-2)^2 & = (5x)^2-2\cdot 5x \cdot 2 + 2^2 \\[2ex] & = 25x^2-20x+4 \end{aligned}$

Demostración de la fórmula del cuadrado de una diferencia

A continuación vamos a deducir de dónde viene la fórmula del cuadrado de una resta. Aunque no es necesario que te aprendas de memoria la demostración, siempre está bien entender las matemáticas que hay detrás de ella.

Si empezamos con la expresión del binomio de una resta cualquiera:

$(a-b)^2$

Evidentemente, la potencia anterior es igual al producto del factor $(a-b)$ multiplicado por sí mismo:

$(a-b)^2= (a-b)\cdot (a-b)$

Ahora multiplicamos los dos paréntesis aplicando la propiedad distributiva:

$\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}$

Y solamente nos queda agrupar los términos semejantes para acabar de demostrar la fórmula:

$a^2-ab-ba+b^2 = a^2-2ab +b^2$

De manera que la fórmula del cuadrado de una resta queda matemáticamente demostrada:

$(a-b)^2=a^2-2ab+b^2$

Como curiosidad, el desarrollo de la expresión del binomio de una resta al cuadrado también se conoce como trinomio cuadrado perfecto.

Interpretación geométrica del cuadrado de una diferencia

Para acabar de comprender el concepto del cuadrado de una diferencia, vamos a ver cómo interpretar geométricamente esta igualdad notable.

Fíjate en el siguiente cuadrado con lados de longitud $a:$

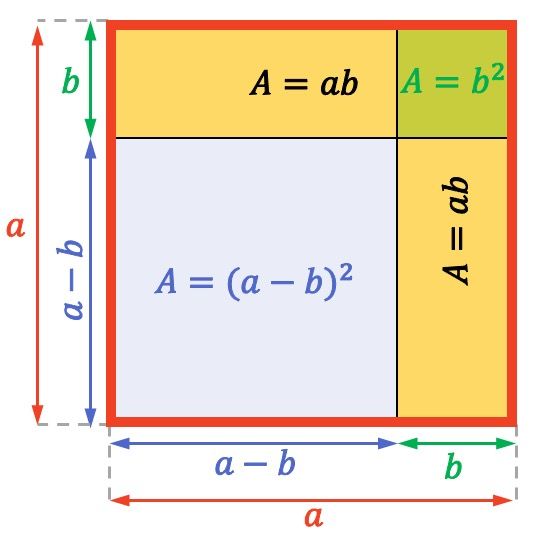
interpretacion geometrica del cuadradado de una diferencia

El área (o superficie) de un cuadrado o un rectángulo se calcula multiplicando dos de sus lados contiguos entre sí. Por tanto, el área de todo el cuadrado entero anterior es $a\cdot a = a^2.$ Del mismo modo, el área de cada rectángulo amarillo es igual a $a\cdot b = ab.$ Y, por último, el cuadrado pequeño representado arriba a la derecha tiene una superficie de $b\cdot b =b^2.$

Esto significa que un cuadrado de lado $(a-b),$ cuya superficie es $(a-b)^2,$ se puede descomponer en el área de un cuadrado de dimensión $a,$ menos 2 veces el área de un rectángulo de dimensiones $a$ y $b$ , más el área de un cuadrado de lado $b.$ En resumen, la fórmula del cuadrado de una diferencia también se puede verificar de forma geométrica:

$(a-b)^2=a^2-2ab+b^2$

Ejercicios resueltos del cuadrado de una diferencia (o resta)

Para que puedas practicar, te dejamos con varios ejercicios resueltos paso a paso sobre el producto notable del cuadrado de una diferencia. Recuerda que puedes escribirnos cualquier duda que tengas abajo en los comentarios.

Ejercicio 1

Resuelve las siguientes restas elevadas al cuadrado:

$\text{A)} \ (x-2)^2$

$\text{B)} \ (3-7x)^2$

$\text{C)} \ \left(x^2-6\right)^2$

$\text{D)} \ (-3x+y)^2$

$\text{E)} \ (4x-3y)^2$

Ver solución

Para hallar todas las identidades notables del problema simplemente debemos aplicar la fórmula del cuadrado de una diferencia, que es:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}$

$\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}$

$\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}$

$\text{E)} \ \begin{aligned}(4x-3y)^2 & = (4x)^2-2\cdot 4x\cdot 3y +(3y)^2\\[2ex] & = \bm{16x^2-24xy+9y^2}\end{aligned}$

Ejercicio 2

Determina los siguientes cuadrados de diferencias de dos cantidades aplicando la fórmula:

$\text{A)} \ \left(6x^3-4y^4\right)^2$

$\text{B)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2$

$\text{C)} \ \displaystyle \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2$

Ver solución

Para determinar todos los productos notables del problema debemos emplear la fórmula de una resta elevada al cuadrado:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2\\[2ex] & = \bm{36x^6-48x^3y^4+16y^8}\end{aligned}$

Para solucionar el apartado B) debes recordar que si se eleva una raíz al cuadrado esta queda simplificada:

$\text{B)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}$

Los monomios de la última resta elevada al cuadrado tienen coeficientes fraccionarios, por lo que para resolverla debemos usar las propiedades de las fracciones:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2 & = \left(\frac{5}{2}x^2\right)^2-2\cdot \frac{5}{2}x^2\cdot \frac{4}{5}x +\left(\frac{4}{5}x\right)^2\\[2ex] & = \frac{5^2}{2^2}x^4-2\cdot \frac{20}{10}x^3 +\frac{4^2}{5^2}x^2 \\[2ex] &= \frac{25}{4}x^4 -2\cdot 2x^3+\frac{16}{25}x^2 \\[2ex] & = \mathbf{\frac{25}{4}} \bm{x^4-4x^3+}\mathbf{\frac{16}{25}}\bm{x^2}\end{aligned}$

Cuadrado de una diferencia (o resta)

¿Qué es el cuadrado de una diferencia (o resta)?

Fórmula del cuadrado de una diferencia (o resta)

Ejemplos de cuadrados de diferencias (o restas)

Ejemplo 1

Ejemplo 2

Demostración de la fórmula del cuadrado de una diferencia

Interpretación geométrica del cuadrado de una diferencia

Ejercicios resueltos del cuadrado de una diferencia (o resta)

Ejercicio 1

Ejercicio 2

Deja un comentario Cancelar respuesta