Descomposición (o expresión) polinómica de un número

En esta página explicamos cómo se hace la descomposición (o expresión) polinómica de un número. Aquí podrás ver ejemplos de descomposiciones polinómicas y, además, encontrarás ejercicios resueltos paso a paso para practicar.

¿Qué es la descomposición polinómica de un número?

En matemáticas, la descomposición polinómica de un número consiste en expresar ese número en una suma, de manera que cada término de la suma sea un producto de cada cifra del número por una potencia de base 10.

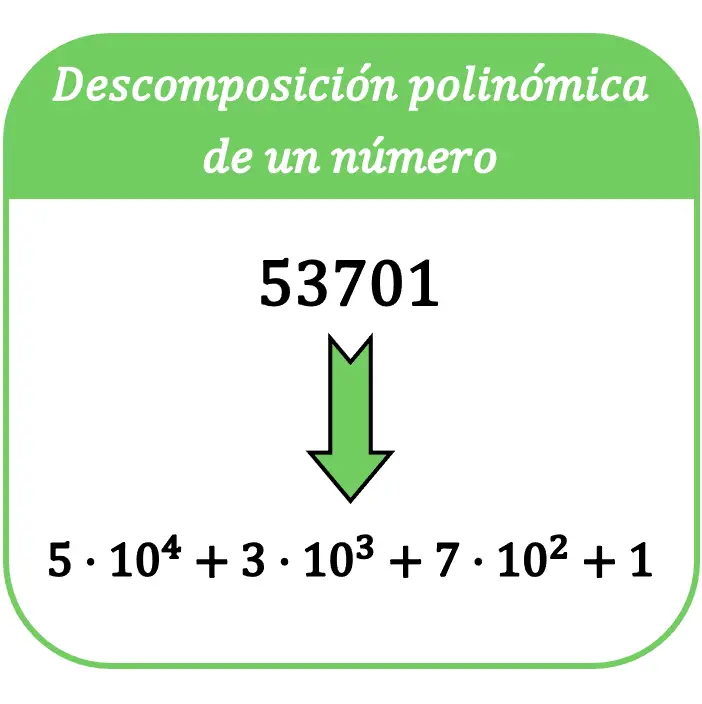
descomposicion polinomica de un numero

El término descomposición polinómica de un número también se conoce como expresión polinómica de un número.

Cómo hacer la descomposición polinómica

Para realizar la descomposición polinómica de un número se debe multiplicar cada cifra del número por 10 elevado a la cantidad de cifras que tiene a la derecha.

Por ejemplo, si queremos calcular la descomposición polinómica del siguiente número:

86293

En este caso, el número 8 ocupa la quinta posición, por lo tanto, tiene 4 cifras a su derecha. Así que debemos multiplicar ocho por diez elevado a la cuatro:

8\cdot 10^4

Entonces, para descomponer polinómicamente el número 86293 debemos hacer lo mismo con todas las cifras del número, y expresar todas las multiplicaciones en forma de suma:

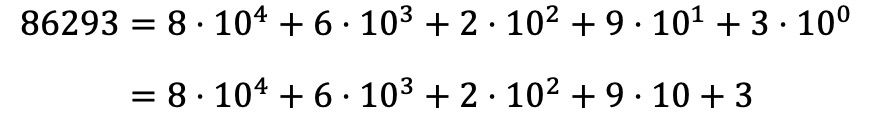
descomposicion polinomica ejemplos

Fíjate que la potencia 100 desaparece porque, según las propiedades de las potencias, cualquier número elevado a 0 es igual a 1, por lo que 100=1.

Por otro lado, también se puede hallar la descomposición polinómica de un número a partir de su descomposición multiplicativa:

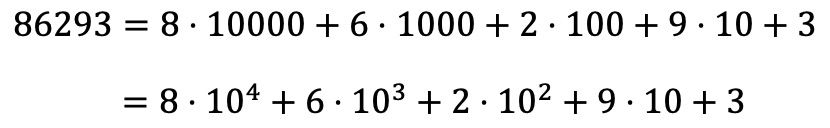
descomposicion polinomica de numeros naturales para primaria

Ejemplos de descomposiciones polinómicas de números

Una vez hemos visto cómo se realiza la descomposición polinómica de un número, vamos a ver diferentes ejemplos de este tipo de operación para acabar de entender el concepto.

  • Descomposición polinómica de 3641:

3641 = 3\cdot 10^3 +6 \cdot 10^2 + 4\cdot 10 + 1

  • Descomposición polinómica de 56912:

56912 = 5\cdot 10^4 +6\cdot 10^3 +9 \cdot 10^2 + 1\cdot 10 + 2

  • Descomposición polinómica de 27084:

\begin{aligned} 27084 &= 2\cdot 10^4 +7\cdot 10^3 +0\cdot 10^2 + 8\cdot 10 + 4 \\[2ex] & = 2\cdot 10^4 +7\cdot 10^3 + 8\cdot 10 + 4 \end{aligned}

En este último ejemplo podemos simplificar la tercera multiplicación ya que cualquier número multiplicado por cero se anula.

Descomposición polinómica de números decimales

Acabamos de ver cómo realizar la descomposición polinómica de números naturales. Pero… ¿cómo se descompone de forma polinómica un número decimal?

Pues la descomposición polinómica con números decimales se hace igual que con los números enteros pero, además, se suma el producto de cada cifra decimal multiplicada por una potencia de base 10 cuyo exponente es la posición decimal que ocupa dicha cifra con signo negativo.

Explicado con palabras puede parecer muy complicado, pero ya verás que con un ejemplo se entiende mejor:

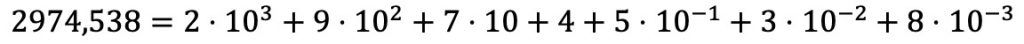
descomposicion polinomio de un numero decimal

Ejercicios resueltos de la descomposición polinómica

Para que puedas practicar de hacer las descomposiciones polinómicas, te hemos preparado varios ejercicios resueltos paso a paso.

¡Recuerda que puedes preguntarnos cualquier duda que tengas en los comentarios! 🤔🤔🤔

Ejercicio 1

Realiza la descomposición polinómica de los siguientes números:

\text{A)} \ 7935

\text{B)} \ 1548

\text{C)} \ 55476

\text{D)} \ 287694

Para encontrar la descomposición polinómica de cualquier número se multiplica cada cifra de dicho número por 10 elevado a la cantidad de cifras que tiene a la derecha, y luego se suman todas las multiplicaciones. Por tanto:

\text{A)} \ 7935 = 7 \cdot 10^3+ 9\cdot 10^2 +3 \cdot 10 +5

 

\text{B)} \ 1548 = 1 \cdot 10^3+ 5\cdot 10^2 +4 \cdot 10 +8

 

\text{C)} \ 55476 = 5\cdot 10^4+ 5 \cdot 10^3+ 4\cdot 10^2 +7\cdot 10 +6

 

\text{D)} \ 287694 = 2\cdot 10^5+8\cdot 10^4+ 7 \cdot 10^3+ 6\cdot 10^2 +9\cdot 10 +4

 

Ejercicio 2

Halla la descomposición polinómica de los siguientes números:

\text{A)} \ 461

\text{B)} \ 3030

\text{C)} \ 11950

\text{D)} \ 8741866

Para descomponer polinómicamente un número se tiene que multiplicar cada cifra de dicho número por diez elevado a la cantidad de cifras que tiene a su derecha, y luego se suman todos los productos. Por tanto:

\text{A)} \ 461 = 4\cdot 10^2 +6 \cdot 10 +1

 

\text{B)} \ \begin{aligned} 3030 & = 3 \cdot 10^3+ 0\cdot 10^2 +3 \cdot 10 +0 \\[2ex] &= 3 \cdot 10^3+3 \cdot 10 \end{aligned}

 

\text{C)} \ 11950 = 1\cdot 10^4+ 1 \cdot 10^3+ 9\cdot 10^2 +5\cdot 10

 

\text{D)} \ 8741866 = 8\cdot 10^6+7\cdot 10^5+4\cdot 10^4+ 1 \cdot 10^3+ 8\cdot 10^2 +6\cdot 10 +6

 

Ejercicio 3

Calcula la descomposición polinómica de los siguientes números decimales:

\text{A)} \ 51,63

\text{B)} \ 249,99

\text{C)} \ 0,82694

\text{D)} \ 5,7201

En este problema todos los números son decimales, de modo que para descomponerlos tenemos que multiplicar cada cifra no decimal por 10 elevado al número de cifras que tiene hasta la coma, y multiplicar cada cifra decimal por 10 elevado a su posición decimal con signo negativo.

\text{A)} \ 51,63 = 5 \cdot 10 +1 + 6 \cdot 10^{-1} +3 \cdot 10^{-2}

 

\text{B)} \ 249,99 = 2\cdot 10^2 + 4 \cdot 10 +9 + 9 \cdot 10^{-1} +9 \cdot 10^{-2}

 

\text{C)} \ \begin{aligned} 0,82694 & = 0 + 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\\[2ex] & = 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\end{aligned}

 

\text{D)} \ \begin{aligned} 5,7201 & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+0\cdot 10^{-3}+1\cdot 10^{-4}\\[2ex] & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+1\cdot 10^{-4} \end{aligned}

 

92 comentarios en “Descomposición (o expresión) polinómica de un número”

    5. Polinomios

      Hola Fanny, aunque sea un número largo, el procedimiento para hallar su expresión polinómica es el mismo:
      2563482=2·106+5·105+6·104+3·103+4·102+8·10+2

    8. Glency

      Saludos. Excelente presentacion…Hay posibilidades de compartir est material o archivo para apoyo en las actividades academicas de mi hijo?. Agradecida

    9. Polinomios

      ¡Muchas gracias Glency!
      Al final de cada post hay unos botones con todas las opciones para compartirlo a través de redes sociales, email, google classroom, etc.
      Y, si estás con el ordenador, también puedes ver estos botones en la barra lateral de la izquierda.

    11. Polinomios

      Si claro Geraldin, te dejo resuelta la descomposición polinómica del número:
      346 718=3·105+4·104+6·103+7·102+1·10+8

    13. Polinomios

      Sin problema Viviana, aquí tienes la descomposición polinómica resuelta:
      7045=7·103+4·10+5

    15. Polinomios

      Hola Cinthya, te descompongo polinómicamente el número decimal a continuación:

      2,345625=2+3·10-1+4·10-2+5·10-3+6·10-4+2·10-5+5·10-6

    7. Polinomios

      Sí, por supuesto Luli, te descompongo el número a continuación:
      123567=1·105+2·104+3·103+5·102+6·10+1

  3. Yuli

    Hola buenas tardes será que por favor me podrás ayudar a descomponer en forma polinómica está cifra 33.099.422.gracias.

    Responder
    1. Polinomios

      Claro Yuli, te lo descompongo a continuación:
      33099422=3·107+3·106+9·104+9·103+4·102+2·10+2

    1. Polinomios

      1850=1·103+8·102+5·10+0

      En este caso el 0 se podría quitar ya que no aporta nada al cálculo:
      1850=1·103+8·102+5·10

    1. Polinomios

      Hola Gabriela, te resuelvo las descomposiciones polinómicas de los números decimales a continuación:
      56796,378=5·104+6·103+7·102+9·10+6+3·10-1+7·10-2+8·10-3
      96733,5469=9·104+6·103+7·102+3·10+3+5·10-1+4·10-2+6·10-3+9·10-4
      38965,432=3·104+8·103+9·102+6·10+5+4·10-1+3·10-2+2·10-3

    1. Polinomios

      Por supuesto Claudia, te resuelvo el ejemplo a continuación:
      4952=4·103+9·102+5·10+2

    3. Polinomios

      Hola Victoria. Sin problema, te lo resuelvo a continuación:
      2428=2·103+4·102+2·10+8

    5. Polinomios

      La expresión polinómica del número que propones es la siguiente:
      7743=7·103+7·102+4·10+3

    7. Polinomios

      Hola Miaaaa, las expresiones polinómicas de los dos números son:

      28,104=2·10+8+1·10-1+4·10-3

      426,03=4·102+2·10+6+3·10-2

  7. Genesis

    Muy buenas noches polinomios, me resolvió muchas dudas, gracias. Por favor me pueden ayudar con este ejercicio: 95.030?

    Responder
    1. Polinomios

      Por supuesto Genesis, te resuelvo el ejercicio a continuación:
      95030=9·104+5·103+3·10

      Ten en cuenta que este número tiene un cero en la cifra de las centenas y de las unidades, por tanto, no hace falta expresarlas en su descomposición polinómica.

    1. Polinomios

      Hola Denny, al descomponer polinómicamente el número obtenemos:
      1109=1·103+1·102+9

  9. jiomary

    excelente la explicación muy detallada me servira de mucho para las tareas de mi hija felicidades y muchisimas gracias por tu ayuda.

    Responder
    1. Polinomios

      Claro Amabys, te resuelvo las dos expresiones polinómicas a continuación:

      a)3456=3·103+4·102+5·10+6

      b)45896=4·104+5·103+8·102+9·10+6

    1. Polinomios

      Claro Mayrim, la expresión polinómica de este número es:
      5481=5·103+4·102+8·10+1

    1. Polinomios

      Las expresiones polinómicas de los cuatro números son las siguientes:

      18985=1·104+8·103+9·102+8·10+5

      59276=5·104+9·103+2·102+7·10+6

      172934=1·105+7·104+2·103+9·102+3·10+4

      7963=7·103+9·102+6·10+3

    1. Polinomios

      Por supuesto Liliana, los descompongo polinómicamente a continuación:

      4963=4·103+9·102+6·10+3

      8564=8·103+5·102+6·10+4

    3. Polinomios

      Hola Richard, en este caso en realidad el número solamente tiene dos cifras, ya que los ceros a la izquierda se pueden suprimir. Por tanto:
      89=8·10+9

  14. Maria

    Me pueden ayudar a averiguar la descomposición polinómica de los siguientes números plis, se los agradecería mucho.
    5232

    Responder
    1. Polinomios

      Sin problema Maria, lo resuelvo a continuación:

      5232=5·103+2·102+3·10+2

    1. Polinomios

      Sí Kelly, este número expresado polinómicamente es:

      781050=7·105+8·104+1·103+5·10

  16. Danbeiker rosales

    Hola buenas tardes me puedes ayudar con las siguientes descomposición polinomica: a) 75.890.000, b) 100345675890767,
    c) 45.780.000, d) 0,3, e) 456.789.000,034, f) 678.898.768.732, g) 543.291.322,35

    Responder
    1. Polinomios

      Por supuesto Danbeiker, te hago todas las descomposiciones polinómicas a continuación:

      a) 75.890.000=7·107+5·106+8·105+9·104

      b) 100.345.675.890.767=1·1014+3·1011+4·1010+5·109+6·108+7·107+5·106+8·105+9·104+7·102+6·10+7

      c) 45.780.000=4·107+5·106+7·105+8·104

      d) 0,3=3·10-1

      e) 456.789.000,034=4·108+5·107+6·106+7·105+8·104+9·103+3·10-2+4·10-3

      f) 678.898.768.732=6·1011+7·1010+8·109+8·108+9·107+8·106+7·105+6·104+8·103+7·102+3·10+2

      g) 543.291.322,35=5·108+4·107+3·106+2·105+9·104+1·103+2·10+2+3·10-1+5·10-2

  17. Cenia Ruiz

    Hola, me podrían por favor descomponer polinomicamente las siguientes cantidades 1064981914, 11078820, 1064997824

    Responder
    1. Polinomios

      Sí Cenia, te resuelvo las tres expresiones polinómicas:

      1064981914=1·109+6·107+4·106+9·105+8·104+1·103+9·102+1·10+4

      11078820=1·107+1·1067·104+8·103+8·102+2·10

      1064997824=1·109+6·107+4·106+9·105+9·104+7·103+8·102+2·10+4

    2. Jesús garcia

      Me pueden ayudar con este número 384000000,108000000,1392000 ,13546676

    3. Polinomios

      Hola Jesús, te hago las descomposiciones polinómicas a continuación:

      384000000=3·108+8·107+4·106
      108000000=1·108+8·106
      1392000=1·106+3·105+9·104+2·103
      13546676=1·107+3·106+5·105+4·104+6·103+6·102+7·10+6

  18. Camila

    Hola me pueden ayudar con la descomposición polinomica de los siguientes números 846.327 – 57.963.426 – 589.326.485 – 2.239.761- 3000 porfavor

    Responder
    1. Polinomios

      Camila, te resolvemos las expresiones polinómicas a continuación:

      846.327=8·105+4·104+6·103+3·102+2·10+7
      57.963.426=5·107+7·106+9·105+6·104+3·103+4·102+2·10+6
      589.326.485=5·108+8·107+9·106+3·105+2·104+6·103+4·102+8·10+5
      2.239.761=2·106+2·105+3·104+9·103+7·102+6·10+1
      3000=3·103

    1. Polinomios

      Hola Nadia, tienes las expresiones polinómicas de todos los números resueltas a continuación:

      846.327 = 8·105+4·104+6·103+3·102+2·10+7

      57.963.426 = 5·107+7·106+9·105+6·104+3·103+4·102+2·10+6

      589.326.485 = 5·108+8·107+9·106+3·105+2·104+6·103+4·102+8·10+5

      2.239.761 = 2·106+2·105+3·104+9·103+7·102+6·10+1

      3.000 = 3·103

    1. Polinomios

      Hola Jasmin, te dejo la expresión polinómica del número a continuación:
      56=5·10+6

    1. Polinomios

      Hola Kiara, entiendo que utilizas la coma como separador decimal, en tal caso la expresión polinómica del número es:
      23,333=2·10+3+3·10-1+3·10-2+3·10-3

      Si la coma se trata simplemente de un separador de millares, entonces la expresión polinómica es:
      23333 = 2·104+3·103+3·102+3·10+3

    1. Polinomios

      Hola Juliana, tienes hechas las dos descomposiciones polinómicas a continuación:

      25369 = 2·104+5·103+3·102+6·10+9

      10912 = 1·104+9·102+1·10+2

  26. Susan

    Hola necesito ayuda con estos números es largo
    5032763
    12467340
    8524433
    25015328
    por favor necesito ayuda🙏🙏

    Responder
    1. Polinomios

      Hola Susan, tienes las descomposiciones polinómicas de los números resueltas a continuación:

      5032763=5·106+3·104+2·103+7·102+6·10+3

      12467340=1·107+2·106+4·105+6·104+7·103+3·102+4·10

      8524433=8·106+5·105+2·104+4·103+4·102+3·10+3

      25015328=2·107+5·106+1·104+5·103+3·102+2·10+8

    1. Polinomios

      Hola Martha, aunque los números sean grandes, el procedimiento es exactamente el mismo. Te dejo las expresiones polinómicas de los tres números resueltas a continuación:

      15.000.731=1·107+5·106+7·102+3·10+1

      35.000.350.001=3·1010+5·109+3·105+5·104+1

      1.500.035.003.258=1·1012+5·1011+3·107+5·106+3·103+2·102+5·10+8

    1. Polinomios

      Hola Max, para descomponer un número debes utilizar alguna base numérica.

  30. Ivana M

    Hola, me podrían ayudar con esta por favor 🙁
    846.099
    9732.293

    Los necesito urgente y no logro entender muy bien 🙁 me ayudarían por favor

    Responder
    1. Polinomios

      Hola Ivana,

      Las descomposiciones polinómicas de los números que propones son las siguientes:

      846099=8·105+4·104+6·103+9·10+9

      9732293=9·106+7·105+3·104+2·103+2·102+9·10+3

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio