En esta página explicamos qué son las fracciones algebraicas, cuándo son equivalentes, cómo simplificarlas y cómo hacer operaciones con fracciones algebraicas (suma, resta, multiplicación y división). Además, podrás ver ejercicios resueltos paso a paso de fracciones algebraicas. En resumen, aquí encontrarás todo sobre las fracciones algebraicas.
Índice
¿Qué son las fracciones algebraicas?
En matemáticas, una fracción algebraica es aquella fracción que tiene un polinomio en el numerador y otro polinomio en el denominador.
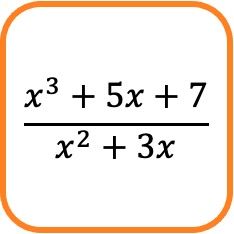
Por ejemplo, la expresión fraccionaria anterior consiste en una fracción algebraica porque tanto su numerador como su denominador están formados por polinomios.
Fracciones algebraicas equivalentes
Una vez ya sabemos la definición de fracciones algebraicas, veamos cuándo dos fracciones de este tipo son iguales.
Matemáticamente, dos fracciones algebraicas son equivalentes si se cumple la siguiente condición:
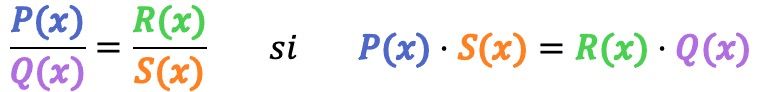
A modo de ejemplo, vamos a verificar si las siguientes 2 fracciones algebraicas son equivalentes:
Para determinar si las fracciones son algebraicamente iguales, multiplicamos sus términos en cruz:
Ahora calculamos las multiplicaciones de polinomios:
Hemos obtenido la misma expresión en ambos lados de la ecuación, por lo tanto, efectivamente se trata de dos fracciones algebraicas equivalentes.
Simplificar fracciones algebraicas
Para simplificar una fracción algebraica primero se deben factorizar los polinomios del numerador y del denominador, y luego eliminar los factores que tengan en común.
Evidentemente, para poder hacer la simplificación de fracciones algebraicas es imprescindible que sepas qué es la factorización de polinomios y cómo se hace. Si aún no sabes cómo se factorizan los polinomios o no te acuerdas del todo, te recomiendo que antes de seguir vayas a la página enlazada, ya que de lo contrario difícilmente entenderás el procedimiento. Allí se explica paso a paso cómo factorizar polinomios y, además, podrás ver varios ejemplos y practicar con ejercicios resueltos.
Ahora sí, veamos cómo se simplifica una fracción algebraica aplicando el método de la factorización de polinomios mediante un ejemplo:
- Simplifica la siguiente fracción algebraica:
Primero de todo, factorizamos los polinomios del numerador y del denominador de la fracción:
⬆(Si no sabes cómo se han factorizado los polinomios échale un vistazo al enlace de arriba)⬆
Y una vez hemos factorizado los polinomios, eliminamos los factores comunes entre el numerador y el denominador, es decir, quitamos todos los términos que se repiten:
De forma que la fracción algebraica simplificada queda de la siguiente manera:
En este problema se han factorizado los polinomios de la fracción algebraica hallando sus raíces, sin embargo, en ocasiones se puede factorizar un polinomio directamente sacando factor común (método mucho más rápido). En este enlace podrás ver en qué consiste sacar factor común de un polinomio y encontrarás cómo simplificar una fracción algebraica mediante factor común.
Operaciones con fracciones algebraicas
Como cualquier tipo de fracciones, también se pueden realizar operaciones con fracciones algebraicas. En concreto, las fracciones algebraicas se pueden sumar, restar, multiplicar y dividir. A continuación explicamos paso a paso con ejemplos cómo se calcula cada tipo de operación.
Suma y resta de fracciones algebraicas
El procedimiento para sumar y restar fracciones algebraicas es prácticamente idéntico, por tanto, los analizaremos de manera conjunta. Primero veremos un ejemplo de dos fracciones algebraicas sumadas y, más abajo, estudiaremos la diferencia que hay con el método de restar fracciones algebraicas.
Suma de fracciones algebraicas
Sumar fracciones algebraicas se hace de la misma manera que con las fracciones normales: primero se reducen las fracciones a común denominador y luego se suman los numeradores.
Vamos a ver cómo se suman las fracciones algebraicas mediante un ejemplo:
Primero factorizamos los denominadores de las fracciones:
Ahora tenemos que hallar el m.c.m. (mínimo común múltiplo) de los denominadores para reducir las fracciones a común denominador.
Truco: el m.c.m. de los denominadores siempre está formado por el producto de los factores que tienen en común elevados al exponente más grande multiplicados por los factores no comunes.
Por ejemplo, en nuestro caso
El factor común entre los denominadores elevado al exponente más grande es
Y el factor no común entre los denominadores es
Por lo tanto, el m.c.m. de los denominadores en este caso es:
De forma que el m.c.m. de los denominadores es así que este será el nuevo denominador de las 2 fracciones.
Una vez hemos encontrado el denominador común, debemos modificar los numeradores. Para ello, seguimos el mismo proceso que en la suma de fracciones normales: para cada fracción dividimos el m.c.m. entre el denominador original y multiplicamos el resultado por el numerador:
De modo que ahora podemos juntar las dos fracciones porque tienen el mismo denominador:
Finalmente, operamos en el numerador. En primer lugar hacemos el producto del monomio por el polinomio:
Luego sumamos en el numerador los términos semejantes:
Normalmente ya estaríamos, pero si nos fijamos bien en este problema aún podemos simplificar más la fracción algebraica sacando factor común en el numerador. Por tanto:
Y de esta manera ya hemos acabado la suma de las dos fracciones algebraicas.
Resta de fracciones algebraicas
Para restar fracciones algebraicas debemos aplicar un procedimiento similar al de la suma de fracciones algebraicas: primero se reducen las fracciones a común denominador y luego se restan los numeradores.
Veamos pues cómo se restan las fracciones algebraicas con un ejemplo:
En primer lugar, tenemos que factorizar los denominadores de ambas fracciones:
Como en la resta de fracciones normales, ahora debemos calcular el m.c.m. (mínimo común múltiplo) de los denominadores para reducir las fracciones a común denominador. En este caso, el m.c.m. de los denominadores es con lo que este será el nuevo denominador de las 2 fracciones.
Ahora aplicamos el mismo proceso que en la resta de fracciones normales: para cada fracción dividimos el m.c.m. entre el denominador original y multiplicamos el resultado por el numerador:
Ahora juntamos las dos fracciones algebraicas ya que poseen el mismo denominador:
Y operamos en el numerador. Primero resolvemos las multiplicaciones polinómicas:
Un error muy habitual en la resta de fracciones algebraicas es olvidarse de poner un paréntesis después de hacer esta multiplicación. Esto sería un error ya que el signo negativo afecta a todos los elementos resultantes del producto, y no solo al primer término.
Hacemos las operaciones de dentro del paréntesis:
Entonces, debido al signo negativo, cambiamos de signo a todos los términos de dentro del paréntesis:
Y, para terminar, agrupamos los monomios semejantes:
Multiplicación de fracciones algebraicas
Para multiplicar fracciones algebraicas primero se factorizan todos los polinomios de dichas fracciones, en segundo lugar se multiplican los numeradores entre sí y los denominadores entre sí, y, por último, se simplifica la fracción obtenida.
Por lo tanto, en realidad el producto de fracciones algebraicas se calcula de manera parecida al producto de fracciones normales.
Veamos entonces cómo se multiplican dos fracciones algebraicas con un ejemplo:
Primero de todo tenemos que factorizar todos los polinomios de las fracciones, tanto de los numeradores como de los denominadores:
Ahora vamos a multiplicar las fracciones. Para ello multiplicamos los numeradores y los denominadores entre sí:
Y finalmente simplificamos los factores que se repiten en el denominador y en el numerador:
De forma que el resultado de la multiplicación es:
La fracción ya no se puede simplificar más. Por lo que ya hemos acabado la multiplicación de las fracciones algebraicas.
División de fracciones algebraicas
Para calcular una división de fracciones algebraicas primero factorizamos todos los polinomios, luego multiplicamos las fracciones en cruz (el primer numerador por el segundo denominador y el primer denominador por el segundo numerador) y, finalmente, simplificamos la fracción algebraica.
Así pues, veamos mejor cómo se dividen dos fracciones algebraicas mediante un ejemplo:
El primer paso para dividir dos fracciones algebraicas es factorizar todos los polinomios que intervienen en la operación:
Ahora tenemos que dividir las fracciones. Para ello, multiplicamos en cruz las fracciones, es decir, el primer numerador se multiplica por el segundo denominador y el resultado será el numerador de la nueva fracción, y, del mismo modo, el primer denominador se multiplica por el segundo numerador y el resultado será el denominador de la nueva fracción:
Simplificamos los factores que se repiten en el denominador y en el numerador:
Y todavía podemos simplificar más la fracción, ya que
La fracción ya no se puede simplificar más. Por tanto, ya hemos dividido las fracciones algebraicas.
Ejercicios resueltos de fracciones algebraicas
A continuación te proponemos varios ejercicios resueltos paso a paso de fracciones algebraicas, para que puedas practicar y así acabar de entender el concepto. ¡Recuerda que puedes preguntarnos cualquier duda que tengas abajo en los comentarios! 💬💬💬
Ejercicio 1
Determina si las siguientes fracciones algebraicas son equivalentes o no:
Para verificar si dos fracciones algebraicas son equivalentes debemos multiplicarlas en cruz y ver si obtenemos una igualdad. Así que primero comprobaremos la primera y la segunda fracción:
Resolvemos la identidad notable de la izquierda de la ecuación:
✅
En este caso hemos obtenido una igualdad, de manera que la primera y la segunda fracción son algebraicamente iguales.
Ahora aplicamos el mismo procedimiento con la primera y la tercera fracción algebraica:
❌
Sin embargo, esta vez las fracciones algebraicas no cumplen con la ecuación, de modo que la primera y la tercera fracción son matemáticamente distintas.
En conclusión, la tercera fracción es diferente a la primera fracción y, en consecuencia, también es desigual a la segunda fracción ya que la primera y la segunda fracción sí que son equivalentes.
Ejercicio 2
Simplifica las siguientes fracciones algebraicas:
Para simplificar una fracción algebraica tenemos que factorizar los polinomios del numerador y del denominador, y después eliminar los factores que se repiten. Por tanto:
Ejercicio 3
Calcula las siguientes sumas y restas de fracciones algebraicas:
Para sumar (o restar) fracciones algebraicas primero debemos reducir las fracciones a común denominador y luego sumar (o restar) los numeradores. Por lo tanto:
Ejercicio 4
Resuelve las siguientes multiplicaciones y divisiones de fracciones algebraicas:
Para multiplicar fracciones algebraicas primero tenemos que factorizar todos los polinomios, luego multiplicamos los numeradores y los denominadores entre sí, y, finalmente, simplificamos la fracción obtenida.
En cambio, para dividir fracciones algebraicas primero factorizamos todos los polinomios, después multiplicamos las fracciones en cruz (el primer numerador por el segundo denominador y el primer denominador por el segundo numerador) y, por último, simplificamos la fracción algebraica hallada.
¿Qué te ha parecido la explicación? ¿Te ha gustado? ¿O tienes alguna sugerencia? 💬 ¡Coméntanos qué piensas de esta página en los comentarios! ¡Os leemos a todos! 👀 ¡Y recuerda que también puedes preguntarnos cualquier duda que tengas! ❔👇❔👇

Interesante, la manera de desarrollar los contenidos. Solo así los estudiantes podrán entenderlos con mas facilidad.
Gracias a ustetes por estar allí
¡Muchas gracias Rafael!