Número combinatorio (o coeficiente binomial)

En esta página explicamos qué es un número combinatorio y cómo se calcula (fórmula). Además, podrás ver ejemplos de cómo calcular cualquier número combinatorio y practicar con ejercicios resueltos paso a paso. También, mostramos todas las propiedades y las aplicaciones de los números combinatorios. Y, para terminar, enseñamos cómo hallar el resultado de un número combinatorio directamente con la calculadora.

¿Qué es un número combinatorio?

En matemáticas, el número combinatorio, también llamado coeficiente binomial, es el número de combinaciones ordinarias (combinaciones sin repetirse) de grupos de k elementos que se pueden formar de un conjunto de n elementos (n>k).

Un número combinatorio se expresa con un paréntesis de la siguiente manera:

\begin{pmatrix}n \\ k \end{pmatrix}

Por otro lado, el número combinatorio se lee n sobre k. Asimismo, n se dice que es el numerador y k recibe el nombre de orden.

Solo con la definición de número combinatorio es difícil entender su significado. Sin embargo, ahora vamos a ver cómo se determina matemáticamente el número combinatorio y luego profundizaremos en este concepto de combinatoria. Ya verás que de esta forma lo entenderás mejor.

Fórmula del número combinatorio

La fórmula que permite calcular el valor de un número combinatorio (o coeficiente binomial) es la siguiente:

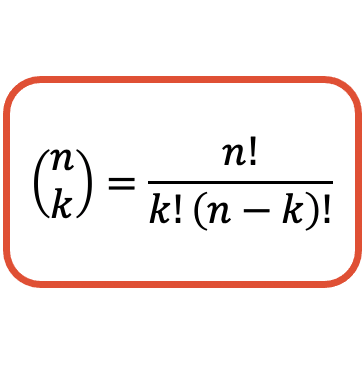
formula del numero combinatorio

Recuerda que en álgebra el signo de exclamación corresponde al factorial de un número. Y para hallar el factorial de un número se deben multiplicar todos los números enteros positivos que hay desde el 1 hasta ese número. Por ejemplo, para calcular el factorial del número 4 debemos hacer la multiplicación de 1, 2, 3 y 4:

4! = 1\cdot 2 \cdot 3 \cdot 4 =24

También es importante que sepas que el factorial de 0 es igual a 1.

0! = 1

Ejemplo de cómo calcular un número combinatorio

A continuación, vamos a determinar el valor de un número combinatorio paso a paso a modo de ejemplo, para que así puedas ver cómo se hace:

  • Calcula el valor del número combinatorio de 5 sobre 3.

El coeficiente binómico de 5 sobre 3 corresponde a la siguiente expresión:

\begin{pmatrix}5 \\ 3 \end{pmatrix}

Por lo tanto, si aplicamos la fórmula del número combinatorio, para determinar su valor debemos hacer las siguientes operaciones:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!(5-3)!}

O, equivalentemente:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!\cdot 2!}

Así que hallamos los factoriales:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{1\cdot 2 \cdot 3 \cdot 4 \cdot 5}{(1\cdot 2 \cdot 3) \cdot (1\cdot 2)}

La multiplicación 1·2·3 se repite tanto en el numerador como en el denominador, por lo que se puede simplificar la fracción eliminando este factor:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{\cancel{1\cdot 2 \cdot 3} \cdot 4 \cdot 5}{(\cancel{1\cdot 2 \cdot 3)} \cdot (1\cdot 2)}

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{ 4 \cdot 5}{1\cdot 2}

Ahora calculamos los productos:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{20}{2}

Y, finalmente, hacemos la división:

\begin{pmatrix}5 \\ 3 \end{pmatrix} = \bm{10}

Propiedades del número combinatorio

Los números combinatorios, o coeficientes binomiales, se pueden combinar según las siguientes propiedades:

  • Dos números combinatorios complementarios son aquellos que tienen el mismo numerador n y la suma de sus órdenes es equivalente a dicho numerador. Así pues, el resultado de dos números combinatorios complementarios es idéntico.

\begin{pmatrix}n \\ k \end{pmatrix} = \begin{pmatrix}n \\ n-k \end{pmatrix}

Esta característica de los números combinatorios también se llama identidad de simetría.

Por ejemplo, 6 sobre 4 da el mismo resultado que 6 sobre 2, porque 6-4=2.

\begin{pmatrix}6 \\ 4 \end{pmatrix} =\cfrac{6!}{4!(6-4)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(\cancel{1\cdot 2 \cdot 3\cdot 4})\cdot (1\cdot 2)}= \cfrac{30}{2} = \bm{15}

\begin{pmatrix}6 \\ 2 \end{pmatrix} =\cfrac{6!}{2!(6-2)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(1\cdot 2)\cdot (\cancel{1\cdot 2 \cdot 3\cdot 4})}= \cfrac{30}{2} = \bm{15}

 

  • La suma de dos números combinatorios con el mismo numerador y órdenes sucesivos es igual a otro número combinatorio cuyo numerador equivale al numerador de los sumandos más 1 y cuyo orden corresponde al mayor valor de los órdenes de los sumandos. Es decir, siempre se cumple la siguiente condición:

\begin{pmatrix}n\\ k \end{pmatrix} + \begin{pmatrix}n\\ k+1 \end{pmatrix}= \begin{pmatrix}n+1\\ k+1 \end{pmatrix}

Por ejemplo:

\begin{pmatrix}9\\ 2 \end{pmatrix} + \begin{pmatrix}9\\ 3 \end{pmatrix}= \begin{pmatrix}10\\ 3 \end{pmatrix}

Esta propiedad también se conoce como regla de Pascal.

Por otra parte, esta fórmula también se puede aplicar a la inversa para descomponer un número combinatorio en dos números combinatorios más simples:

\begin{pmatrix}n\\ k \end{pmatrix} = \begin{pmatrix}n-1\\ k-1 \end{pmatrix}+ \begin{pmatrix}n-1\\ k \end{pmatrix}

Por ejemplo, el número combinatorio 8 sobre 4 es igual a 7 sobre 3 más 7 sobre 4:

\begin{pmatrix}8\\ 4 \end{pmatrix} = \begin{pmatrix}7\\ 3 \end{pmatrix}+ \begin{pmatrix}7\\ 4 \end{pmatrix}

 

  • Cualquier número positivo sobre 1 es igual al propio número.

\begin{pmatrix}n\\ 1 \end{pmatrix} =n

El motivo de esta propiedad es que el factorial de un número es igual al factorial del número anterior por el propio número:

\begin{pmatrix}n \\ 1 \end{pmatrix} =\cfrac{n!}{1!(n-1)!} = \cfrac{n\cdot (n-1) \cdot (n-2)\cdots 1}{(n-1) \cdot (n-2)\cdots 1}= n

Ejemplos de este tipo de números combinatorios:

\begin{pmatrix}12\\ 1 \end{pmatrix} =12 \qquad \begin{pmatrix}5\\ 1 \end{pmatrix} =5 \qquad \begin{pmatrix}9\\ 1 \end{pmatrix} =9

 

  • Cualquier número positivo sobre 0 es igual a la unidad.

\begin{pmatrix}n\\ 0 \end{pmatrix} =1

Esto se debe a que el denominador de la fracción de tal número combinatorio siempre equivaldrá al numerador de la fracción:

\begin{pmatrix}n\\ 0 \end{pmatrix} =\cfrac{n!}{0!(n-0)!} =\cfrac{n!}{n!} = 1

Ejemplos de números combinatorios como este:

\begin{pmatrix}6\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}2\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}23\\ 0 \end{pmatrix} =1

 

  • Todo número sobre si mismo es igual a 1.

\begin{pmatrix}n\\ n \end{pmatrix} =1

Aquí tienes la demostración:

\begin{pmatrix}n\\ n \end{pmatrix} =\cfrac{n!}{n!(n-n)!} =\cfrac{n!}{n!\cdot 0!}= \cfrac{n!}{n!} = 1

Ejemplos de números combinatorios así:

\begin{pmatrix}5\\ 5 \end{pmatrix} =1 \qquad \begin{pmatrix}37\\ 37 \end{pmatrix} =1 \qquad \begin{pmatrix}14\\ 14 \end{pmatrix} =1

Cómo calcular un número combinatorio con la calculadora

Hasta ahora hemos visto cómo encontrar un número combinatorio de números más o menos sencillos, pero cuando tengamos que operar con cantidades muy grandes es mejor que utilicemos la calculadora para determinar el número combinatorio. De manera que ahora vamos a ver cómo poner un número combinatorio en la calculadora.

Así pues, la tecla que sirve para calcular un número combinatorio con la calculadora es la tecla nCr. Y para determinar el valor del número combinatorio primero se debe introducir el numerador del número combinatorio, en segundo lugar pulsar la tecla nCr, luego introducir el orden del número combinatorio y, por último, pulsar la tecla del igual.

\begin{pmatrix}n\\ k \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} n \rightarrow \boxed{nCr} \rightarrow k \rightarrow \boxed{=}

En las calculadoras científicas CASIO normalmente la tecla nCr tiene un propio botón o está encima del botón de dividir, dependiendo del modelo.

Por ejemplo, si queremos averiguar cuánto vale el número combinatorio 10 sobre 6 tenemos que hacer la siguiente secuencia:

\begin{pmatrix}10\\ 6 \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} 10 \rightarrow \boxed{nCr} \rightarrow 6 \rightarrow \boxed{=} \rightarrow 210

Aplicaciones del número combinatorio

Si has llegado hasta aquí seguro que ya sabes resolver cualquier número combinatorio, perfecto. Pero… ¿para qué sirve el número combinatorio? Pues bien, seguidamente veremos todas las utilidades que tiene este tipo de operación tan especial.

Combinatoria

Como hemos visto al principio de la página, el resultado de un número combinatorio \begin{pmatrix}n\\ k \end{pmatrix} representa el número de posibles grupos de k elementos que se pueden hacer de un conjunto de un total de n elementos.

Por lo tanto, algunos problemas de combinatoria se pueden solucionar a través de números combinatorios (o coeficientes binomiales). Veamos cómo hacerlo mediante un ejemplo:

  • En una clase de 30 alumnos se quiere escoger un grupo formado por 4 alumnos para que hagan algunas tareas. ¿Cuál es el número total de grupos distintos que se pueden hacer?

En este caso, el orden de los alumnos no importa, no se repite un mismo alumno dos veces dentro del grupo, y no entran todos los alumnos en el grupo. Por lo tanto, se puede emplear la fórmula del número combinatorio para determinar de cuántas maneras se puede hacer el grupo.

Para ello, debemos calcular el número combinatorio con el número total de alumnos como numerador y con el número de alumnos que formarán el grupo como orden:

\begin{pmatrix}30 \\ 4 \end{pmatrix} =\cfrac{30!}{4!(30-4)!} =\cfrac{30\cdot 29 \cdot 28 \cdot 27 \cdot \cancel{26!}}{4\cdot 3 \cdot 2 \cdot 1 \cdot \cancel{26!}} = \cfrac{657720}{24}=\bm{27405}

De modo que el número total de combinaciones posibles es 27405 grupos.

Binomio de Newton

Otra aplicación de los números combinatorios es el binomio de Newton. El binomio de Newton es un polinomio compuesto por dos términos elevados conjuntamente a un número entero, es decir, el binomio de Newton es aquel polinomio que cumple con la siguiente expresión algebraica:

(a+b)^n

Evidentemente, si el binomio está elevado al cuadrado significa que es una identidad notable y, por tanto, se puede calcular fácilmente con su correspondiente fórmula. Por contra, cuando el binomio está elevado a números grandes el cálculo se dificulta bastante. Pues bien, el teorema del binomio de Newton dice que se pueden calcular este tipo de polinomios de una manera muy fácil a partir de los números combinatorios.

Haz click en el siguiente enlace y descubre cuál es la fórmula del binomio de Newton y cómo se calcula. Además, podrás ver ejemplos y practicar con ejercicios resueltos paso a paso. Y, por último, encontrarás la curiosa historia de este teorema.

Triángulo de Tartaglia (o de Pascal)

Como has podido comprobar a lo largo de todo este artículo, calcular el coeficiente binomial de números grandes a mano puede ser laborioso y complicado.

En cambio, con el triángulo de Tartaglia, o también llamado triángulo de Pascal, se pueden determinar todos los números combinatorios fácilmente con una regla mnemotécnica. Esto lógicamente es muy útil ya que te permite ahorrarte mucho tiempo al hacer los cálculos.

Para saber exactamente cómo se hace, consulta la explicación del triángulo de Tartaglia. En esta página enlazada encontrarás qué es este triángulo tan misterioso, para qué sirve (tiene aplicaciones sorprendentes) 😮 y cuál es su origen (ya se utilizaba hace más de 1000 años).

Ejercicios resueltos de números combinatorios

Para que puedas practicar y entender del todo los conceptos explicados, te dejamos con varios ejercicios resueltos paso a paso sobre números combinatorios.

Ejercicio 1

Halla el número combinatorio 9 sobre 5 (sin usar las calculadora).

Para encontrar el valor del número combinatorio 9 sobre 5 simplemente aplicamos la fórmula de los factoriales:

\begin{pmatrix}9 \\ 5 \end{pmatrix} =\cfrac{9!}{5!(9-5)!} = \cfrac{9\cdot 8 \cdot 7\cdot 6\cdot \cancel{5!}}{\cancel{5!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{3024}{24} = \bm{126}

 

Ejercicio 2

¿Cuál es el resultado de la siguiente suma de dos números combinatorios? (sin calculadora)

\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}

A partir de las propiedades de los números combinatorios, se deduce que la suma del problema es igual al siguiente número combinatorio:

\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}=\begin{pmatrix}11\\ 7 \end{pmatrix}

En consecuencia, solo es necesario calcular el número combinatorio 11 sobre 7:

\begin{pmatrix}11 \\ 7 \end{pmatrix} =\cfrac{11!}{7!(11-7)!} = \cfrac{11\cdot 10 \cdot 9\cdot 8 \cdot \cancel{7!}}{\cancel{7!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{7920}{24} = \bm{330}

 

Ejercicio 3

Determina si son iguales los siguientes números combinatorios:

\begin{pmatrix}6\\ 0 \end{pmatrix} \qquad \begin{pmatrix}6\\ 1 \end{pmatrix}\qquad \begin{pmatrix}6\\ 6 \end{pmatrix}

Para hallar el resultado de los tres números combinatorios no hace falta utilizar la calculadora, sino que se pueden averiguar fácilmente con las propiedades de los números combinatorios.

Primero de todo, un número combinatorio de cualquier número sobre 0 da como resultado 1. Por tanto:

\begin{pmatrix}6\\ 0 \end{pmatrix} =1

Por otro lado, todo número sobre la unidad es igual al propio número. Por tanto:

\begin{pmatrix}6\\ 1 \end{pmatrix} =6

Y, finalmente, cualquier número combinatorio formado por el mismo número repetido dos veces es equivalente a 1. Por tanto:

\begin{pmatrix}6\\ 6 \end{pmatrix} =1

En conclusión, el primer y el tercer número combinatorio del problema son iguales entre sí, en cambio, son diferentes al número combinatorio del medio.

\begin{pmatrix}6\\ 0 \end{pmatrix}= \begin{pmatrix}6\\ 6 \end{pmatrix}\neq \begin{pmatrix}6\\ 1 \end{pmatrix}

 

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio