En esta página explicamos cómo se hacen todas las operaciones con monomios (suma, resta, multiplicación, división y potencia). Además, podrás ver ejemplos de cada tipo de operación con monomios y practicar con ejercicios resueltos paso a paso.
Índice
Suma y resta de monomios
Dos o más monomios solo se pueden sumar o restar si son monomios semejantes, es decir, si ambos monomios tienen una parte literal idéntica (mismas letras y mismos exponentes).
Entonces, la suma (o resta) de dos monomios semejantes es igual a otro monomio compuesto por la misma parte literal y la suma (o resta) de los coeficientes de esos dos monomios.
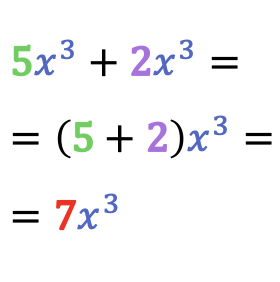
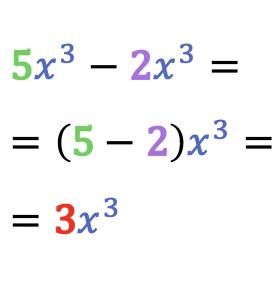
La suma y resta de monomios también se llaman adición y sustracción de monomios respectivamente.
Ejemplos de sumas y restas de monomios
Para que puedas entender del todo cómo sumar y restar dos o más monomios, a continuación te dejamos con varios ejemplos:
Los monomios del último ejemplo no se pueden ni sumar ni restar porque los monomios no son semejantes, o dicho de otra forma, tienen diferentes incógnitas o exponentes.
Producto de un número por un monomio
Para resolver el producto de un monomio por un número simplemente se debe multiplicar el coeficiente del monomio por dicho número, quedando la parte literal del monomio igual.
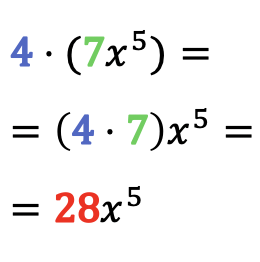
Ejemplos de multiplicaciones de números por monomios
Multiplicación de monomios
El resultado de la multiplicación de dos monomios es otro monomio cuyo coeficiente es el producto de los coeficientes de los monomios y cuya parte literal se obtiene de multiplicar las variables que tienen la misma base, es decir, sumando sus exponentes.
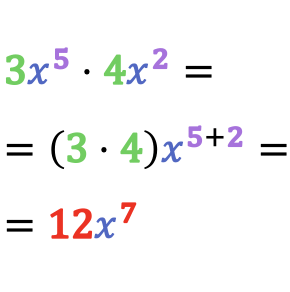
Por lo tanto, para multiplicar dos monomios diferentes se deben multiplicar los coeficientes entre sí y sumar los exponentes de las potencias que tengan la misma base.
Sin embargo, si multiplicamos dos monomios con alguna potencia de base distinta, simplemente tenemos que multiplicar sus coeficientes entre sí y dejar las potencias igual. Por ejemplo:
Por otro lado, en la multiplicación de monomios hay que tener en cuenta la regla de los signos:
- Un monomio positivo multiplicado por un monomio positivo da como resultado otro monomio positivo.
- Un monomio positivo por un monomio negativo (o viceversa) es igual a un monomio negativo.
- Dos monomios negativos multiplicados entre sí dan lugar a un monomio positivo.
Ejemplos de multiplicaciones de monomios
A continuación tienes con varios ejemplos de la multiplicación entre monomios para que puedas ver cómo se hace:
Como has visto, resolver una multiplicación de monomios es relativamente fácil. Pero debes tener en cuenta que los monomios también se pueden multiplicar por polinomios, e incluso 2 o más polinomios se pueden multiplicar entre sí. Si estás más interesado, puedes ver cómo se hacen todas estas operaciones haciendo click en multiplicación de polinomios.
División de monomios
En matemáticas, el resultado de la división de monomios es otro monomio cuyo coeficiente equivale al cociente de los coeficientes de los monomios y cuya parte literal se obtiene de dividir las variables que tienen la misma base, es decir, restando sus exponentes.
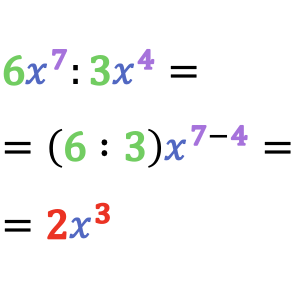
Evidentemente, cualquier división de monomios también se puede expresar en forma de fracción:
Al igual que en la multiplicación, en la división de monomios hay que aplicar la ley de los signos:
- Un monomio positivo dividido por un monomio positivo da como resultado otro monomio positivo.
- Un monomio positivo entre un monomio negativo (o viceversa) es igual a un monomio negativo.
- Dos monomios negativos divididos entre sí dan lugar a un monomio positivo.
Ejemplos de divisiones de monomios
Puedes ver más ejemplos de cómo se dividen dos o más monomios a continuación:
Seguro que alguna vez cuando has aprendido algo nuevo en matemáticas te has preguntado: ¿y para qué demonios sirve esto? Pues la división de monomios se utiliza para dividir polinomios, de hecho, es bastante frecuente equivocarse dividiendo polinomios porque se han dividido mal dos monomios. Por eso te recomendamos que, ahora que tienes fresca la división entre monomios, veas cómo se calcula la división de polinomios, ya que ahora te será mucho más fácil aprender el procedimiento (es bastante complicado).
Potencia de un monomio
En matemáticas, para calcular la potencia de un monomio se eleva cada elemento del monomio al exponente de la potencia. Es decir, la potencia de un monomio consiste en elevar su coeficiente y sus variables (letras) al exponente de la potencia.
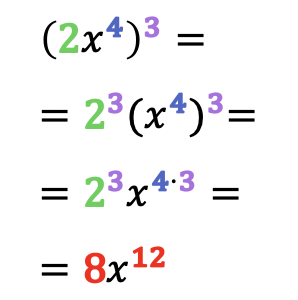
Recuerda de las propiedades de las potencias que cuando elevamos un término que ya está elevado los dos exponentes se multiplican entre sí. Por eso en la potencia de un monomio siempre se multiplica el exponente de cada letra por el exponente que indica la potencia.
Por otra parte, para hacer bien esta operación debes recordar la siguiente propiedad de las potencias:
- Un monomio negativo elevado a un exponente par es equivalente a un monomio positivo.
- En cambio, un monomio negativo elevado a un exponente impar da como resultado un monomio negativo.
Ejemplos de potencias de monomios
Te dejamos con varios ejemplos para que puedas comprender del todo cómo se calcula la potencia de un monomio:
Operaciones combinadas con monomios
Una vez ya has visto cuáles son todas las operaciones con monomios, debes saber que también se pueden combinar entre sí. Es decir, nos podemos encontrar ejercicios en los que nos pidan de resolver operaciones con monomios donde intervengan todos los tipos: sumas, restas, multiplicaciones, divisiones y potencias.
Pero no te preocupes, no son tan difíciles como aparentan. Lo único que debes recordar es el orden con el que se resuelven las operaciones combinadas:
- Primero se resuelven las operaciones con monomios de dentro de los paréntesis.
- Luego se calculan las potencias de monomios.
- En tercer lugar se hacen las multiplicaciones y las divisiones de monomios.
- Y, finalmente, se determinan las sumas y las restas de monomios.
Seguro que resolviendo un ejemplo lo ves más claro:
Ejemplo de operación combinada de monomios
Primero de todo, debemos resolver las operaciones con monomios de los paréntesis:
En este caso no tenemos ninguna potencia. Así que ahora calculamos las multiplicaciones y las divisiones de monomios:
Y, por último, hacemos las sumas y las restas de monomios:
Ejercicios resueltos de operaciones con monomios
Por si quieres practicar, a continuación te dejamos varios ejercicios resueltos paso a paso de dificultad de la ESO sobre operaciones con monomios.
Ejercicio 1
Calcula las siguientes sumas y restas de monomios:
Ejercicio 2
Resuelve las siguientes multiplicaciones de monomios:
Ejercicio 3
Determina el resultado de las siguientes divisiones de monomios:
En la operación anterior hemos simplificado el término porque cualquier número elevado a 0 es igual a 1. Por lo tanto:
Ejercicio 4
Halla las siguientes potencias de monomios:
Ejercicio 5
Resuelve las siguientes operaciones combinadas con monomios y simplifica al máximo:
No se puede simplificar más la operación porque los dos monomios tienen exponentes diferentes, por lo que el resultado es un polinomio.
Si has llegado hasta aquí significa que ya dominas todas las operaciones con monomios. ¡Genial! Pues otra operación que seguramente te interese es el factorial de un número. Se trata de una operación bastante curiosa, ya que se calcula de manera diferente a cualquier otra. Y, de hecho, mucha gente no sabe qué es el factorial de un número. Descubre cómo se resuelve un factorial haciendo click en este enlace.


Me ha gustado mucho me parece muy útil pero yo pondría otras formas de hacerse aparte de esas ya que pueden resultar mas fáciles o útiles.
Gracias por tu aportación Adriana.
¡Te animo a compartir aquí cómo lo haces tú para aportar más a todos!
En el primer ejercicio en el apartado Z la respuesta esta errónea puesto a que en el enunciado hay un -8x. y en la corrección un -8xz.
Toda la razón, en el enunciado faltaba la z. Muchas gracias por notificar este pequeño error. 🙂
Gracias, mañana tenía una examen.
Eres muy buena profesora o eso creo yo.💛💛💛
¡Gracias a ti Darío! ❤ ¡Seguro que te ha ido bien el examen! 💪
Excelente forma tan didáctica de transmitir el conocimiento, me ayudaste a recordar lo que aprendí hace mas de 20 años, y si a eso le sumo la dificultad de escribir con los exponenciales y simbología en el ambiente windows, es un doble merito.
Muchas felicidades y que Dios te bendiga!
¡Muchas gracias Jorge! ¡Nos esforzamos para hacer fáciles las matemáticas! 😉
Aprendí aca en 20 minutos lo que no aprendí en 11 años de escuela, gracias
¡Qué bueno Vanesa!
Gracias por la ayuda, me sirvió de mucho.
¡Me alegro Limcy! ¡Gracias por tu comentario!
graccias por todo, pe ha ayudado mucho
¡Muchas gracias Jorge!
mi profe de matematicas no le entiendo pero aqui entendi gracias por ayudarme
Gracias