¿Cómo calcular las raíces de un polinomio? (ejercicios resueltos)

En esta página encontrarás qué son las raíces de un polinomio y cómo se calculan. Además, podrás ver ejemplos y ejercicios resueltos paso a paso sobre las raíces de un polinomio.

Índice

¿Qué son las raíces de un polinomio?

En matemáticas, las raíces (o ceros) de un polinomio son los valores que anulan el polinomio. Es decir, las raíces de un polinomio son todos aquellos valores que cuando se evalúan en el polinomio su valor numérico es igual a 0.

En definitiva, $x=a$ es una raíz del polinomio $P(x)$ si $P(a)=0.$

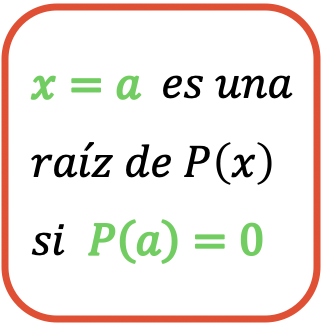
Por ejemplo, si tenemos el siguiente polinomio:

$P(x)=x^2-3x+2$

Podemos comprobar que una de las raíces del polinomio es 1, ya que el valor numérico del polinomio en x=1 es igual a cero:

$P(1)=1^2-3\cdot 1+2 = 1-3+2 \color{blue} \bm{= 0}$

En cambio, 3 no es una raíz del polinomio porque no es un valor que anule al polinomio, o dicho de otra forma, el valor numérico del polinomio en x=3 es diferente de cero:

$P(3)=3^2-3\cdot 3+2 = 9-9+2=2 \color{blue} \bm{\neq 0}$

Seguro que ahora ya entiendes mejor qué es la raíz de un polinomio, pero ¿no te gustaría saber cuántas raíces tiene un polinomio? ¿O cómo encontrar todas las raíces de un polinomio? Pues esto es precisamente lo que vamos a ver en el siguiente apartado.

¿Cómo calcular todas las raíces de un polinomio?

Para hallar todas las raíces de un polinomio se deben seguir los siguientes pasos:

Primero se calculan todos los divisores del término independiente del polinomio.
En segundo lugar, se evalúan en el polinomio todos los valores encontrados en el paso anterior.
Finalmente, si al evaluar un número en el polinomio su valor numérico es igual a cero, dicho número es una raíz del polinomio. De lo contrario, dicho número no corresponde a una raíz del polinomio.

Este procedimiento se deduce del teorema del resto, haz click en este enlace para descubrir el porqué de este peculiar procedimiento.

Ejemplo de cómo se calculan las raíces de un polinomio

A continuación vamos a resolver un ejemplo paso a paso para que puedes comprender mejor cómo sacar las raíces de un polinomio.

¿Cuáles son todas las raíces del siguiente polinomio?

$P(x) = x^2-5x+6$

Primero de todo, debemos encontrar los divisores del término independiente, porque cualquier raíz de un polinomio también es un divisor del término independiente. Así pues, los divisores de 6 son:

Divisores de 6: +1, -1, +2, -2, +3, -3

Recuerda que si un número es un divisor, su negativo también lo es. Ya que un número es divisible por números positivos y negativos.

De manera que las posibles raíces o ceros del polinomio son: ±1, ±2, ±3. Por lo tanto, debemos determinar el valor numérico del polinomio en todos esos valores. Y, para ello, sustituimos dichos valores en la expresión del polinomio donde haya una x:

$P(1) = 1^2 -5\cdot 1 +6= 1 -5 +6 =2$

$P(-1) = (-1)^2 -5\cdot (-1) +6 =1+5+6 = 12$

$P(2) = 2^2 -5\cdot 2 +6 =4-10+6= \color{blue} \bm{0}$

$P(-2) = (-2)^2 -5\cdot (-2) +6 =4+10+6 =20$

$P(3) = 3^2 -5\cdot 3 +6 =9-15+6=\color{blue} \bm{0}$

$P(-3) = (-3)^2 -5\cdot (-3) +6 =9+15+6 =30$

De modo que el polinomio se anula solamente cuando la variable x vale +2 o +3, así que estas son las raíces del polinomio:

Raíces o ceros del polinomio: +2 y +3

Por otro lado, fíjate que el polinomio tienes tantas raíces como su grado, es decir, como el polinomio es de segundo grado tiene dos raíces. En las propiedades de las raíces de un polinomio (más abajo), veremos por qué siempre se cumple esta característica para cualquier polinomio.

Acabamos de ver una manera para hallar las raíces de un polinomio. Sin embargo, aún existen más métodos para conseguirlo, por ejemplo también se pueden encontrar las raíces de un polinomio con la regla de Ruffini. Haz click en el siguiente enlace para ver ejemplos de la regla de Ruffini, aquí encontrarás en qué consiste este método tan conocido y, además, cuáles son las diferencias entre los dos procedimientos.

Propiedades de las raíces de un polinomio

Las raíces o ceros de un polinomio tienen las siguientes características:

Como hemos visto antes, las raíces (o ceros) enteras de un polinomio son divisores del término independiente del polinomio.

Si conocemos todas las raíces de un polinomio, podemos expresar dicho polinomio en forma de productos de binomios del tipo $(x-a).$

Por ejemplo, el polinomio $P(x) =x^3+3x^2-x-3$ tiene 3 raíces, que son $x=+1, x=-1$ y $x=-3.$ Por lo tanto, podemos reescribir el polinomio en forma de 3 multiplicaciones de factores, cada uno formado por la variable $x$ y una raíz cambiada de signo:

$\displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}$

$\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60}P(x) =x^3+3x^2-x-3 = (x\color{verd}\bm{-1}\color{black})\cdot (x\color{vermell}\bm{+1}\color{black}) \cdot (x\color{blau}\bm{+3}\color{black})$

A esto se le llama factorización de polinomios. De hecho, una de las aplicaciones principales de determinar las raíces de un polinomio es que sirven para poderlo factorizar. En el siguiente enlace podrás saber en qué consiste esta operación tan especial y, además, podrás practicar con ejercicios resueltos de factorización de polinomios.

Un polinomio tiene tantas raíces como indica su grado. Por lo que un polinomio de segundo grado tendrá 2 raíces, un polinomio de tercer grado tendrá 3 raíces, un polinomio de cuarto grado tendrá 4 raíces, y así sucesivamente.

Si un polinomio no tiene término independiente significa que una de sus raíces es 0. Entonces, el resto de raíces deben ser divisores del coeficiente del monomio de menor grado.

Por ejemplo, el siguiente polinomio no tiene término indendiente:

$P(x) =x^3+x^2-2x$

De modo que una raíz del polinomio debe ser necesariamente 0. Y el resto de raíces son divisores del coeficiente del término de menor grado, es decir -2. En concreto, las otras raíces son $x=+1$ y $x=-2,$ por lo que todas las raíces del polinomio son:

Raíces o ceros del polinomio: 0, +1 y -2

Cuando no se pueden determinar las raíces de un polinomio, decimos que es un polinomio irreducible.

Por ejemplo, vamos a intentar calcular las raíces del siguiente polinomio:

$P(x) =x^2+3x-1$

Las únicas posibles raíces del polinomio son los divisores de -1, es decir -1 y +1. Así que evaluamos el polinomio en dichos valores:

$P(1) = 1^2 +3\cdot 1 -1= 1 +3 -1 =3 \neq 0$

$P(-1) = (-1)^2 +3\cdot (-1)-1 =1-3-1 =-3 \neq 0$

En ningún caso se anula el polinomio, por tanto no tiene raíces y, en consecuencia, es un polinomio irreducible.

Cuando el polinomio está compuesto por el producto de varios polinomios no es necesario realizar dicho producto para calcular las raíces, sino que las raíces del polinomio son las raíces de cada factor que está multiplicando.

A modo de ejemplo, si tenemos el siguiente polinomio:

$P(x) = (x-2) \cdot (x+1)$

A partir de la segunda propiedad de las raíces de los polinomios, podemos deducir que la raíz del polinomio de la izquierda es +2 y la raíz del polinomio de la derecha es -1.

$\displaystyle (x-2) \ \longrightarrow \ \text{ra\'iz} \ x=+2$

$\displaystyle (x+1) \ \longrightarrow \ \text{ra\'iz} \ x=-1$

Por lo tanto, las raíces del polinomio resultante de la multiplicación de ambos factores son sus respectivas raíces, es decir, +2 y -1.

$\displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}$

Ejercicios resueltos de raíces de polinomios

Ejercicio 1

Determina si $x = -4$ es una raíz del siguiente polinomio:

$P(x)=x^3+2x^2-11x-12$

Ver solución

Para saber si $x=-4$ es una raíz del polinomio debemos evaluarlo en ese valor. Por tanto:

$\begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}$

El valor numérico del polinomio en $x=-4$ es nulo, así que efectivamente se trata de una raíz del polinomio.

Ejercicio 2

Calcula todas las raíces del siguiente polinomio:

$P(x)=x^2-3x+2$

Ver solución

En primer lugar, para hallar las posibles raíces del polinomio tenemos que encontrar los divisores del término independiente. Así pues, los divisores de 2 son:

Divisores de 2: +1, -1, +2, -2

De forma que las posibles raíces o ceros del polinomio son ±1 y ±2. Por lo tanto, debemos calcular cuánto vale el polinomio en todos esos valores:

$P(1)=1^2-3\cdot 1+2 =1-3+2=0$

$P(-1)=(-1)^2-3\cdot (-1)+2 =1+3+2=6$

$P(2)=2^2-3\cdot 2+2 =4-6+2=0$

$P(-2)=(-2)^2-3\cdot (-2)+2 =4+6+2=12$

De manera que el polinomio se anula cuando x vale +1 o +2, así que estas son las raíces del polinomio:

Raíces o ceros del polinomio: +1 y +2

Ejercicio 3

Halla las raíces del siguiente polinomio:

$P(x)=x^3-x^2-4x+4$

Ver solución

Primeramente debemos encontrar los divisores del término independiente, ya que la raíz de un polinomio también es un divisor del término independiente. Así pues, los divisores de 4 son:

Divisores de 4: +1, -1, +2, -2, +4, -4

De forma que las posibles raíces o ceros del polinomio son ±1, ±2 y ±4. Por lo tanto, debemos hallar el valor numérico del polinomio en todos esos valores:

$P(1)=1^3-1^2-4\cdot 1+4 =1-1-4+4=0$

$P(-1)=(-1)^3-(-1)^2-4\cdot (-1)+4 =-1-1+4+4=6$

$P(2)=2^3-2^2-4\cdot 2+4 =8-4-8+4=0$

$P(-2)=(-2)^3-(-2)^2-4\cdot (-2)+4 =-8-4+8+4=0$

$P(3)=3^3-3^2-4\cdot 3+4 =27-9-12+4=10$

$P(-3)=(-3)^3-(-3)^2-4\cdot (-3)+4 =-27-9+12+4=20$

De modo que el polinomio se anula únicamente cuando x vale +1, +2 o -2, así que estas son las raíces del polinomio:

Raíces o ceros del polinomio: +1, +2 y -2

Ejercicio 4

Encuentra las raíces del siguiente polinomio:

$P(x)=x^3-6x^2+8x$

Ver solución

En este caso, el polinomio no tiene término independiente. Por tanto, según la cuarta propiedad de las raíces explicada más arriba, sabemos que una de las raíces del polinomio tiene que ser 0.

Raíces del polinomio: $x=0$

Además, en este caso las posibles raíces no son los divisores del término independiente, sino los del coeficiente del término de menor grado, o sea 8:

Divisores de 8: +1, -1, +2, -2, +4, -4, +8, -8

De forma que las posibles raíces o ceros del polinomio son ±1, ±2, ±4 y ±8. Por lo tanto, debemos calcular el valor numérico del polinomio en todos esos valores:

$P(1)=1^3-6\cdot 1^2+8\cdot 1 = 1-6+8=3$

$P(-1)=(-1)^3-6\cdot (-1)^2+8\cdot (-1) = -1-6-8=-15$

$P(2)=2^3-6\cdot 2^2+8\cdot 2 = 8-24+16=0$

$P(-2)=(-2)^3-6\cdot (-2)^2+8\cdot (-2) = -8-24-16=-48$

$P(4)=4^3-6\cdot 4^2+8\cdot 4 = 64-96+32=0$

$P(-4)=(-4)^3-6\cdot (-4)^2+8\cdot (-4) = -64-96-32=-192$

$P(8)=8^3-6\cdot 8^2+8\cdot 8 = 512-384+64=192$

$P(-8)=(-8)^3-6\cdot (-8)^2+8\cdot (-8) = -512-384-64=-960$

De modo que el polinomio se anula cuando x vale +2 o +4, por lo que estos valores son raíces del polinomio. Sin embargo, también tenemos que añadir la raíz 0 que hemos encontrado al principio del problema. En conclusión, todas las raíces del polinomio son:

Raíces o ceros del polinomio: 0, +2 y +4

Ejercicio 5

Utiliza las propiedades de las raíces de los polinomios para calcular las raíces del siguiente polinomio:

$P(x)=(x-1)(x+3)(x^2-x-2)$

Ver solución

Como hemos visto en la sexta propiedad de las raíces, cuando el polinomio está formado por el producto de factores no hace falta calcular todas las raíces, ya que las raíces de todo el polinomio son las raíces de cada factor.

Además, a partir de la segunda propiedad de las raíces de los polinomios, podemos deducir que la raíz del primer factor es +1 y la raíz del segundo factor es -3.

$\displaystyle (x-1) \ \longrightarrow \ \text{ra\'iz} \ x=+1$

$\displaystyle (x+3) \ \longrightarrow \ \text{ra\'iz} \ x=-3$

Por lo tanto, solo nos queda encontrar las raíces del último factor. Para ello, hallamos los divisores del término independiente (-2):

Divisores de -2: +1, -1, +2, -2

De forma que las posibles raíces o ceros del último polinomio son ±1 y ±2. Con lo que debemos calcular el valor numérico de dicho polinomio en todos esos valores:

$q(x)= x^2-x-2$

$q(1)=1^2-1-2=1-1-2=-2$

$q(-1)=(-1)^2-(-1)-2=1+1-2=0$

$q(2)=2^2-2-2=4-2-2=0$

$q(-2)=(-2)^2-(-2)-2=4+2-2=4$

De manera que las raíces del polinomio de la derecha son -1 y 2.

Por tanto, las raíces del polinomio entero son todas las raíces halladas:

Raíces o ceros del polinomio: +1, -1, +2, -3

8 comentarios en “Raíces de un polinomio”

Julio Medina
27/04/2021 a las 12:23

Buenos dias pueden ayudarme con este ejercicio de polinomios que no tiene término independendiente y con cuando es impar
Q(x)= 5×4 – 7×3 + 11x + k
P(x)= 4×4 + 10×3 + 19x + 5

Responder
1. Polinomios
  02/05/2021 a las 11:41
  
  Hola Julio, sí te podemos ayudar, ¿pero podrías definir el ejercicio un poco más? No se entiende qué pide el ejercicio.
rosa
05/05/2021 a las 00:26

puede aydame en este ejercicio
-5x-25

Responder
1. Polinomios
  06/05/2021 a las 11:29
  
  La única raíz de este polinomio es x=-5.
  
  Puedes comprobar que este valor es una raíz del polinomio calculando el valor numérico:
  -5·(-5)-25=25-25=0
Samuel
07/05/2021 a las 07:48

Buenas noches, será que me pueden ayudar con este ejercicio se los agradezco muchísimo (bueno en realidad son 3):
1)X² – 6x + 5 = 0
2)6x² + 5x – 21 = 0
3)x² + 3x + 2 = 0

Responder
1. Polinomios
  11/05/2021 a las 23:11
  
  Claro Samuel, te resuelvo los ejercicios a continuación. Se ha aplicado el procedimiento que explicamos en el post:
  1) x=5 ; x=1
  2) x=3/2 ; x=-7/3. En este caso el polinomio no tiene raíces enteras, por lo que deberás resolver la ecuación de segundo grado para hallar sus raíces.
  3) x=-1 ; x=-2
Claudia
06/01/2022 a las 23:20

Buenas tardes, podrían explicarme éste ejercicio: 1/2x-3= 5/x + 3/2x*2-3x

Responder
1. Polinomios
  07/01/2022 a las 12:44
  
  Hola Claudia,
  
  Se trata de una ecuación con fracciones algebraicas. Para ver cómo se resuelven este tipo de ecuaciones te aconsejo ir a nuestra página web de ejerciciosecuaciones.com.

¿Qué son las raíces de un polinomio?

¿Cómo calcular todas las raíces de un polinomio?

Ejemplo de cómo se calculan las raíces de un polinomio

Propiedades de las raíces de un polinomio

Ejercicios resueltos de raíces de polinomios

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

8 comentarios en “Raíces de un polinomio”

Deja un comentario Cancelar respuesta