▷ Fórmula del cuadrado de una suma ✅ (con ejercicios resueltos)

En esta página encontrarás cuál es la fórmula del cuadrado de una suma, es decir, de la identidad notable (a+b)². También podrás ver ejemplos y ejercicios resueltos de sumas al cuadrado. Y, además, descubrirás las propiedades geométricas que esconde este producto notable.

Índice

¿Qué es el cuadrado de una suma?

El cuadrado de una suma es una de las identidades notables (o productos notables), por lo tanto, se trata de una regla matemática que permite calcular de manera rápida la potencia de un binomio con dos términos positivos elevado cuadrado.

Así pues, el cuadrado de una suma consiste en dos términos diferentes sumados y elevados al cuadrado, es decir, la expresión algebraica del cuadrado de una suma es (a+b)².

Fórmula del cuadrado de una suma

Vista la definición matemática de este tipo de identidad notable, vamos a ver ahora cuál es la fórmula del cuadrado de una suma:

De modo que el cuadrado de una suma es igual al cuadrado del primer término, más el doble del producto del primero por el segundo, más el cuadrado del segundo.

Entonces, para resolver una suma al cuadrado no es suficiente con elevar cada sumando a la dos, sino que, además, se debe multiplicar los dos sumandos entre sí y por 2.

Es importante que recuerdes esto, porque un error que se comete muy habitualmente al hacer cuadrados de sumas es olvidarse del producto entre los dos términos y calcular solamente los cuadrados:

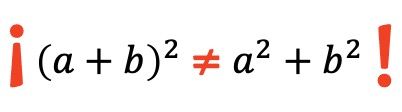
¡Recuerda no dejarte ningún término de la fórmula!

Por otro lado, recuerda que la fórmula de una resta al cuadrado (o cuadrado de una resta) es muy similar a la que acabamos de ver, pero tiene una diferencia que cambia totalmente el resultado. Por si no tienes del todo claro cómo es, puedes consultar aquí cuál es la fórmula de una resta al cuadrado y cómo se aplica.

Ejemplos de cuadrados de sumas

A continuación tienes varios ejemplos resueltos para que puedas ver cómo se hace el cuadrado de una suma:

Ejemplo 1

Calcula la siguiente suma al cuadrado aplicando la fórmula:

$(x+5)^2$

La fórmula de una suma al cuadrado es:

$(a+b)^2=a^2+2ab+b^2$

Por lo tanto, primero de todo tenemos que identificar los parámetros $a$ y $b$ de la fórmula. En este caso, $a$ representa la $x$ del binomio y $b$ corresponde al número 5:

$\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}$

Pues como ahora ya sabemos los valores de $a$ y de $b,$ podemos aplicar la fórmula para hallar el resultado del cuadrado de la suma:

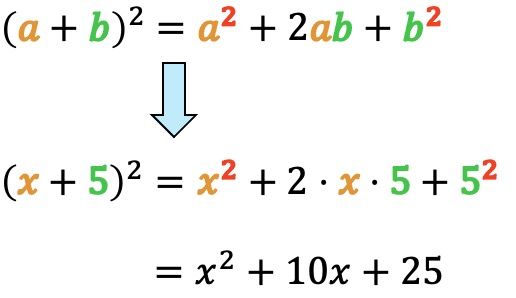
Ejemplo 2

Resuelve la siguiente expresión del cuadrado de una suma:

$(3x+4)^2$

La fórmula del cuadrado de una suma es:

$(a+b)^2=a^2+2ab+b^2$

De modo que en este problema $a$ es el monomio $3x$ y, por otro lado, $b$ es el término independiente 4:

$\begin{array}{c} a=3x \\[2ex] b=4 \end{array}$

Finalmente, una vez hemos identificado los valores de $a$ y de $b$ , aplicamos la fórmula de una suma al cuadrado para resolver el producto notable:

$\begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}$

Demostración de la fórmula del cuadrado de una suma

Seguidamente vamos a hacer la deducción de la fórmula que acabamos de ver del cuadrado de una suma, para que así entiendas de dónde viene.

Partiendo de un binomio positivo elevado a la 2:

$(a+b)^2$

La potencia anterior es, evidentemente, equivalente al factor $(a+b)$ multiplicado por sí mismo:

$(a+b)^2=(a+b)\cdot (a+b)$

Entonces, multiplicamos los dos paréntesis utilizando la propiedad distributiva:

$\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}$

Por último, de los términos resultantes agrupamos los que son semejantes:

$a^2+ab+ba+b^2 = a^2+2ab+b^2$

Y ya hemos llegado a la expresión polinómica de la fórmula, por lo que queda demostrada:

$(a+b)^2= a^2+2ab+b^2$

Aunque puede resultar difícil de creer, la fórmula del cuadrado de una suma también sirve para factorizar polinomios de segundo grado. Por si no sabes en qué consiste, la factorización de polinomios es un procedimiento que se utiliza a menudo en matemáticas para simplificar la expresión de un polinomio. Descubre cómo se hace haciendo click en el enlace anterior.

Interpretación geométrica del cuadrado de una suma

Hasta ahora hemos visto cómo se calcula matemáticamente el cuadrado de una suma, pero este producto notable también se puede interpretar geométricamente.

Fíjate en el siguiente cuadrado cuyos lados miden $a+b:$

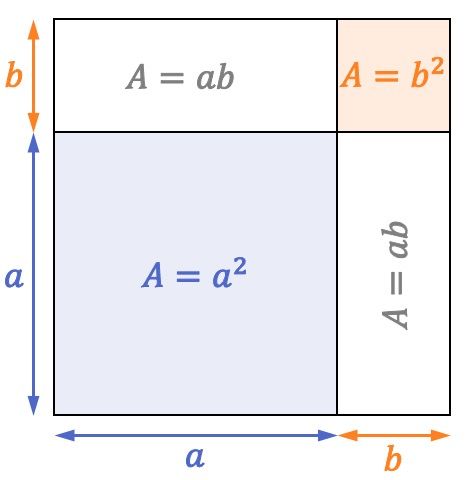
interpretacion geometrica cuadrado de una suma

El área de un cuadrado es equivalente a la longitud de uno de sus lados elevada al cuadrado. En consecuencia, com el lado del cuadrado anterior es $a+b,$ su área (o superfície) es igual a $(a+b)^2.$

Pues, tal y como puedes ver en la representación del cuadrado, dentro de él caben un cuadrado de área $a^2,$ dos rectángulos de área $ab,$ y otro cuadrado de área $b^2.$ Por lo tanto, también se cumple la fórmula de la suma de una cuadrado desde un punto de vista geométrico:

$(a+b)^2=a^2+2ab+b^2$

Ejercicios resueltos del cuadrado de una suma

A continuación te dejamos con varios ejercicios resueltos paso a paso de sumas de cuadrados para que puedas practicar y así acabar de comprender el concepto. Puedes escribirnos cualquier duda que tengas en los comentarios, que la contestaremos encantados. 💭💭💭

Ejercicio 1

Determina las siguientes sumas elevadas al cuadrado:

$\text{A)} \ (x+3)^2$

$\text{B)} \ (2+6x)^2$

$\text{C)} \ \left(x^2+7\right)^2$

$\text{D)} \ (5x+8y)^2$

Ver solución

Para solucionar todas las identidades notables del problema simplemente tenemos que aplicar la fórmula del cuadrado de una suma:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}$

$\text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}$

Ejercicio 2

Resuelve los siguientes cuadrados de sumas de dos términos aplicando la fórmula:

$\text{A)} \ \left(4x^2+2y^3\right)^2$

$\text{B)} \ \displaystyle \left(\sqrt{2x}+\sqrt{8x}\right)^2$

$\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2$

Ver solución

Para calcular todos los productos notables del problema debemos emplear la fórmula de una suma elevada al cuadrado:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}$

En el apartado B) debes recordar que si se eleva una raíz al cuadrado esta se simplifica:

$\text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}$

Los monomios de la última suma elevada al cuadrado tienen coeficientes fraccionarios, por lo que para resolverla también tenemos que utilizar las propiedades de las fracciones:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}$

Ejercicio 3

Halla la siguiente potencia aplicando la fórmula del cuadrado de una suma y sin utilizar la calculadora:

$17^2$

Ver solución

En primer lugar, el número diecisiete se puede descomponer en la suma de 10 más 7:

$17^2=(10+7)^2$

De forma que hemos convertido la potencia en una suma al cuadrado. Por tanto, ahora podemos aplicar la fórmula correspondiente:

$\begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}$

En definitiva, el resultado de la potenciación es:

$17^2=\bm{289}$

Como has podido comprobar en este ejercicio, la fórmula de la suma al cuadrado también sirve para calcular potencias de números grandes sin necesidad de usar la calculadora.

Cuadrado de una suma de 3 términos

En ocasiones nos podemos encontrar con que debemos resolver el cuadrado de tres términos sumados, esto es, (a+b+c)². Lógicamente, en estos casos no podemos emplear la fórmula que hemos explicado, ya que dentro del paréntesis tenemos un trinomio en lugar de un binomio. Por lo que debemos usar otra fórmula distinta.

La fórmula del cuadrado de la suma de 3 términos es la siguiente:

$\definecolor{blauquadreejemplo}{HTML}{ff5733} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=blauquadreejemplo, boxrule=1.2pt, boxsep=2.5mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2.5mm}{-2.5mm}{0mm}{blauquadreejemplo!20!white,} ]}]{equation*} (a+b+c)^2 = a^2+2a(b+c)+b^2+2bc+c^2 \end{empheq}$

Veamos cómo se aplica esta fórmula mediante un ejemplo:

$\begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}$

Como puedes comprobar, al añadir un elemento en la fórmula el resultado se complica mucho más.

2 comentarios en “Cuadrado de una suma (o suma al cuadrado)”

Jackelyn Sánchez
19/11/2021 a las 13:03

Muchas gracias gran ayudar excelente se los recomiendo

Responder
1. Polinomios
  25/11/2021 a las 09:42
  
  ¡Gracias a ti por la recomendación Jackelyn!

¿Qué es el cuadrado de una suma?

Fórmula del cuadrado de una suma

Ejemplos de cuadrados de sumas

Ejemplo 1

Ejemplo 2

Demostración de la fórmula del cuadrado de una suma

Interpretación geométrica del cuadrado de una suma

Ejercicios resueltos del cuadrado de una suma

Ejercicio 1

Ejercicio 2

Ejercicio 3

Cuadrado de una suma de 3 términos

2 comentarios en “Cuadrado de una suma (o suma al cuadrado)”

Deja un comentario Cancelar respuesta