En esta página explicamos qué es el teorema del factor. Además, mostramos para qué sirve el teorema del factor: divisibilidad de polinomios, hallar raíces, factorizar polinomios,… Finalmente, podrás practicar con ejercicios resueltos paso a paso sobre el teorema del factor.
Índice
¿Qué es el teorema del factor?
En matemáticas, el teorema del factor dice que un polinomio P(x) es divisible por otro polinomio de la forma (x-a) si y solo si P(a)=0.
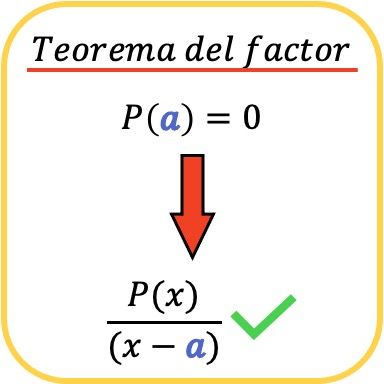
Asimismo, a consecuencia del teorema del factor se deduce que si un polinomio P(x) es divisible entre el término (x−a), significa que el valor a es una raíz (o cero) del polinomio P(x).
Que un polinomio sea divisible entre otro quiere decir que el resto (o residuo) de la división entre los dos polinomios es igual a cero. Por si no recuerdas del todo este concepto en el siguiente enlace puedes ver ejemplos de divisiones de polinomios, allí también encontrarás la explicación de cómo dividir polinomios y ejercicios resueltos paso a paso.
Ejemplos del teorema del factor
Ahora que ya sabemos la definición matemática del teorema del factor, vamos a ver varios ejemplos para ver cómo se aplica.
Ejemplo 1
Una de las aplicaciones del teorema del factor es averiguar si un determinado polinomio es divisible entre un binomio. Veamos un ejemplo de cómo se hace esto con el teorema del factor:
- Determina si el polinomio P(x) es divisible entre el binomio Q(x), siendo ambos:
En primer lugar, el polinomio divisor, Q(x), se trata de un polinomio del tipo (x-a), por lo tanto, podemos aplicar el teorema del factor para resolver el problema.
Entonces, para comprobar si se puede dividir P(x) entre Q(x) tenemos que calcular el valor numérico del polinomio P(x) para x=1, ya que 1 es el término independiente del polinomio divisor cambiado de signo:
![\begin{aligned} P(1) & =1^2-4\cdot 1+3 \\[2ex] & = 1-4+3 \\[2ex] & = 0 \end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-5b84123466cce96a9e6f41708bf78bb1_l3.svg "Rendered by QuickLaTeX.com")
El valor numérico del polinomio P(x) en x=1 da como resultado cero, por lo que según el teorema del factor P(x) es divisible entre Q(x), o dicho con otras palabras, el resto de la división entre ambos será nulo.
Podemos verificar que se cumple la condición de divisibilidad dividiendo los 2 polinomios con el teorema de Ruffini:
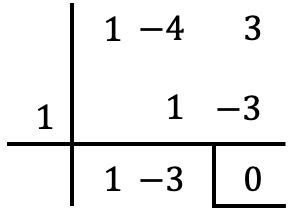
Como puedes ver en este ejemplo, el teorema del factor se trata de un caso especial del teorema del resto (o del residuo). Te dejo este artículo en el que se explica qué es teorema del residuo, también encontrarás ejemplos y ejercicios resueltos con él. Y, además, podrás ver cuál es la diferencia entre el teorema del resto y el teorema del factor.
Ejemplo 2
El teorema del factor también sirve hallar las raíces (o ceros) de un polinomio. Pero, evidentemente, para entender este tipo de problema debes saber qué son las raíces de un polinomio. Si aún no dominas este concepto puedes echarle un vistazo a la página enlazada, que se explica detalladamente.
Veamos pues mediante un ejemplo cómo se aplica el teorema del factor para encontrar una raíz de un polinomio:
- Dado el polinomio P(x), calcula si una de sus raíces es x=2:
Aplicando el teorema del factor, el término x=2 será una raíz del polinomio P(x) solamente si el valor numérico de P(x) para x=2 es nulo. De modo que debemos hallar dicho valor numérico:
![\begin{aligned} P(2) & =2^3-3\cdot 2^2+5\cdot 2-6 \\[2ex] & = 8-3\cdot 4 +5\cdot 2 -6\\[2ex] & = 8-12+10-6 \\[2ex] & = 0\end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-6f0550ff8f81e8442b9d88b6752e494c_l3.svg "Rendered by QuickLaTeX.com")
Efectivamente, el valor numérico del polinomio P(x) se anula en x=2, así que gracias al teorema del factor podemos afirmar que x=2 se trata de una raíz del polinomio P(x).
Factorización de polinomios utilizando el teorema del factor
Otra aplicación del teorema del factor es la factorización de polinomios. Por si no sabes en qué consiste, factorizar un polinomio significa transformar la expresión de un polinomio en un producto de factores, es decir, al factorizar un polinomio se simplifica su expresión algebraica.
Así pues, el teorema del factor establece que si un polinomio P(x) cumple P(a)=0 para un determinado valor a, entonces se puede factorizar la expresión de dicho polinomio en el producto P(x)=(x-a)·Q(x), siendo Q(x) el polinomio resultante de dividir el polinomio P(x) entre (x-a).
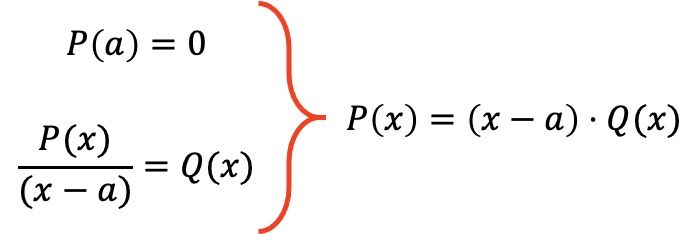
A modo de ejemplo, vamos a factorizar el siguiente polinomio mediante el teorema del factor:
Del polinomio anterior podemos saber que x=-2 es una de sus raíces, ya que el valor numérico del polinomio para x=-2 es igual a cero:
![\begin{aligned} P(-2) & =(-2)^3+2\cdot (-2)^2+4\cdot (-2)+8 \\[2ex] & =-8+2\cdot 4+4\cdot (-2)+8 \\[2ex] & = -8+8-8+8 \\[2ex] & = 0 \end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-f286814f3849a87d8dfce33b1b62ef53_l3.svg "Rendered by QuickLaTeX.com")
Por tanto, dividimos con la regla de Ruffini el polinomio P(x) entre el binomio formado por x y esta raíz cambiada de signo, esto es, el factor (x+2):
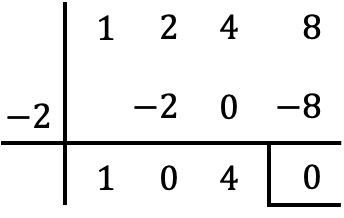
De forma que el cociente de la división polinómica es:
Y, por último, a partir del teorema del factor, podemos expresar el polinomio P(x) en forma de multiplicación del factor (x+2) por el cociente obtenido en la división anterior:
De esta manera hemos factorizado el polinomio P(x), pero solo parcialmente. Para poder factorizar un polinomio completamente se debe aplicar un procedimiento más largo. Nosotros hemos hecho una guía donde enseñamos cómo factorizar polinomios por Ruffini paso a paso, además, en este artículo hemos explicado todos los tipos de factorizaciones y podrás practicar con ejercicios resueltos. Así que haz click en el enlace para descubrir cómo se factoriza un polinomio del todo.
Ejercicios resueltos del teorema del factor
A continuación, hemos elaborado varios ejercicios resueltos paso a paso sobre el teorema del factor para que puedas practicar, y así comprobar si has entendido bien este teorema. Te recomendamos que intentes hacerlos por tu cuenta y luego mires si lo has hecho bien con la solución. ¡Recuerda también que puedes dejarnos cualquier duda abajo en los comentarios! ❓❓💬💬
Ejercicio 1
Halla con el teorema del factor si el polinomio P(x) es divisible por el binomio Q(x) y, en tal caso, halla una raíz del polinomio y factorízalo.
En este caso el polinomio divisor Q(x) es un binomio compuesto solamente por una x y un término independiente. Así que para demostrar que se puede dividir el polinomio P(x) entre el otro polinomio Q(x) con el teorema del factor, debemos evaluar el valor numérico del polinomio P(x) en el término independiente del polinomio divisor cambiado de signo, es decir, en x=3:
![\begin{aligned} P(3) & =2\cdot 3^3-4\cdot 3^2+3-7\\[2ex] & = 2\cdot 27-4\cdot 9+3-7 \\[2ex] & = 54-36+3-7\\[2ex] & = 14 \end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-e0eba5420472ac299bfb1c8ebdd3ff53_l3.svg "Rendered by QuickLaTeX.com")
El valor numérico del polinomio P(x) en x=3 es equivalente a 14, o dicho con otras palabras, es diferente de cero. Con lo que según el teorema del factor, P(x) NO es divisible entre Q(x) porque el resto de la división no es nulo.
Ejercicio 2
Averigua por el teorema del factor si el polinomio P(x) es divisible por el binomio Q(x) y, en dicho caso, halla una raíz del polinomio P(x) y factorízalo.
En este caso el polinomio divisor Q(x) es un binomio compuesto solamente por una x y un término independiente, de manera que podemos aplicar el teorema del factor.
Y para verificar si se puede dividir el polinomio P(x) entre el polinomio Q(x), debemos hallar el valor numérico del polinomio P(x) para el término independiente del polinomio Q(x) cambiado de signo, es decir, en x=-1:
![\begin{aligned} P(-1) & =(-1)^3+5\cdot (-1)^2+3\cdot (-1)-1\\[2ex] & = -1+5\cdot 1+3\cdot (-1)-1\\[2ex] & = -1+5-3-1\\[2ex] & = 0 \end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-aec3cb8b9677a068491eacbe93ec83f4_l3.svg "Rendered by QuickLaTeX.com")
En este problema el valor numérico del polinomio en x=-1 sí que es nulo, así que P(x) es divisible entre Q(x).
Luego, podemos deducir por el teorema del factor que x=-1 es una raíz del polinomio P(x), ya que el valor numérico de P(x) en x=-1 se anula.
Entonces, como x=-1 es una raíz del polinomio P(x), para factorizarlo simplemente tenemos que dividirlo entre x+1. Y, para ello, utilizaremos el método de Ruffini:
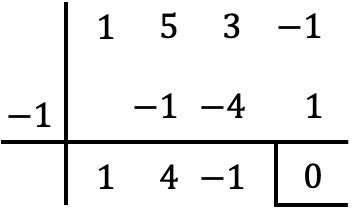
De modo que el resultado de la operación es:
Por lo tanto, podemos factorizar el polinomio P(x) de la siguiente manera:
Ejercicio 3
Encuentra con el teorema del factor si el polinomio P(x) es divisible por el binomio Q(x) y, en tal caso, encuentra también una raíz del polinomio P(x) y factorízalo.
En este caso el polinomio que está dividiendo Q(x) es un binomio formado únicamente por una x y un término independiente, por lo que podemos emplear el teorema del factor.
Y para corroborar si el polinomio P(x) es divisible entre el polinomio Q(x), debemos determinar el valor numérico del polinomio P(x) para el término independiente del polinomio Q(x) cambiado de signo, es decir, en x=-3:
![\begin{aligned} P(-3) & =(-3)^3+5\cdot (-3)^2+4\cdot (-3)-6\\[2ex] & = -27+5\cdot 9+4\cdot (-3)-6\\[2ex] & = -27+45-12-6\\[2ex] & = 0 \end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-206527762e4bf1d196b70000746e6585_l3.svg "Rendered by QuickLaTeX.com")
En este caso el valor numérico del polinomio en x=-3 es nulo, por tanto, efectivamente P(x) es divisible entre Q(x).
Por este motivo, deducimos por el teorema del factor que x=-3 es una raíz del polinomio P(x), debido a que P(-3) es igual a cero.
Entonces, como x=-3 es una raíz del polinomio P(x), para factorizarlo tenemos que dividirlo entre x+3. Y, para ello, usaremos la regla de Ruffini:
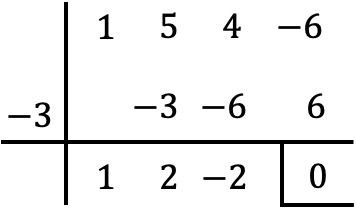
De manera que el resultado de la división es:
Y, en consecuencia, podemos factorizar el polinomio P(x) de la siguiente manera:
¿Qué te ha parecido el teorema del factor? ¿Crees que es útil en álgebra? ¡Os leemos en los comentarios!
👀⬇⬇⬇👀
