Aquí encontrarás la explicación de cómo se resuelve el producto notable de un binomio al cubo (fórmula), ya sea (a+b)3 o (a-b)3. Además, podrás ver ejemplos y ejercicios resueltos paso a paso de binomios al cubo.
Índice
¿Qué es un binomio al cubo?
Un binomio al cubo es un polinomio formado por dos términos elevado a la 3. Por lo tanto, la expresión algebraica de un binomio al cubo puedes ser (a+b)3 o (a-b)3, dependiendo de si se suman o se restan sus monomios.
Además, el binomio elevado al cubo forma parte de las identidades notables (o productos notables). En concreto, corresponde a una de las identidades notables al cubo (o cúbicas).
Fórmula del binomio al cubo
Como hemos visto en la definición de binomio al cubo, este tipo de identidad notable puede consistir en una suma o una resta. En consecuencia, la fórmula varia ligeramente en función de si se trata de un binomio positivo o de un binomio negativo y, por tanto, veremos cada caso por separado.
Cubo de una suma
Cuando una suma está elevada al cubo, la podemos calcular mediante la fórmula del cubo de una suma:

De forma que un binomio al cubo (suma) es igual al cubo del primero, más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo.
Otro método para calcular el cubo de un binomio es mediante el binomio de Newton (o teorema del binomio). Te dejamos el siguiente enlace con la explicación de este teorema porque resulta bastante útil saber esta fórmula, ya que no solo sirve para potencias de binomios de tercer grado, sino también para exponentes más altos. Así que haz click en este enlace para descubrirla y poder practicar con ejercicios resueltos del binomio de Newton.
Cubo de una diferencia
Por otro lado, si en lugar de una suma tenemos una diferencia (o resta) elevada al cubo, la fórmula del binomio al cubo cambia en el signo de los términos pares:

Por lo tanto, un binomio al cubo (resta) es equivalente al cubo del primero, menos el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, menos el cubo del segundo.
De manera que lo único en que se distinguen las fórmulas del cubo de una suma y del cubo de una diferencia es en los signos del segundo y del cuarto término, ya que en el binomio de una suma todos son positivos y, por contra, en el binomio de una resta ambos son negativos.
Acabemos de ver qué son el binomio suma y el binomio diferencia. Pues bien, debes saber que la suma por diferencia de dos binomios también es una identidad notable y, de hecho, es una de las 3 principales (más importantes). Puedes ver cuál es la fórmula de una suma por una diferencia y cómo se aplica en la página enlazada.
Ejemplos de binomios al cubo
Ahora que ya sabemos cuál es la fórmula del cubo de una suma y la fórmula del cubo de una diferencia, vamos a ver un ejemplo de cómo resolver cada tipo de binomio al cubo para acabar de entender el concepto.
Ejemplo del cubo de una suma
- Resuelve el siguiente binomio al cubo aplicando la fórmula:
En este problema tenemos un binomio cuyos dos términos son positivos. Por tanto, tenemos que aplicar la fórmula de una suma elevada al cubo:
Ahora debemos averiguar el valor de los parámetros y
de la fórmula. En este caso,
corresponde a la variable
y
es el número 2.
Por tanto, calculamos el binomio al cubo sustituyendo los valores de y de
en la fórmula:
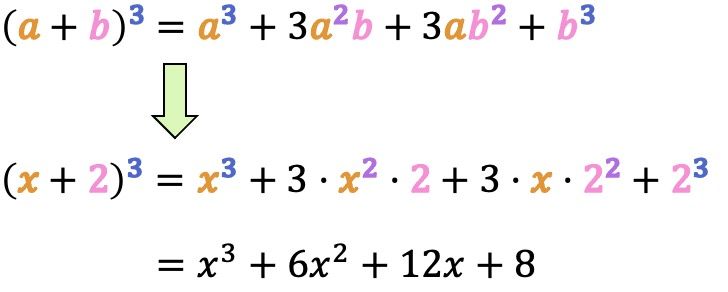
Ejemplo del cubo de una diferencia
- Calcula el siguiente binomio al cubo (diferencia) utilizando su correspondiente fórmula:
En este ejercicio tenemos un binomio con un elemento positivo y otro negativo. Por lo que debemos usar la fórmula de una diferencia elevada al cubo:
Entonces, tenemos que identificar el valor de las incógnitas y
de la fórmula. En este caso,
representa el monomio 3x y
es el término independiente del binomio, es decir, 2.
Fíjate que el parámetro equivale simplemente a 2, sin el signo negativo del número. Es importante tener esto en cuenta para aplicar bien la fórmula.
Finalmente, resolvemos el binomio al cubo poniendo los valores de y de
en la fórmula:
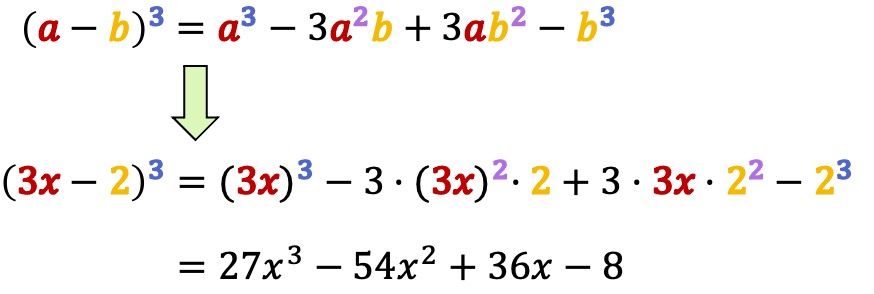
Demostración de la fórmula del binomio al cubo
A continuación vamos a demostrar la fórmula de un binomio al cubo. Aunque evidentemente no es necesario saberla, siempre está bien entender el álgebra que hay detrás de cualquier fórmula.
Partiendo de un binomio positivo al cubo:
La expresión anterior se puede descomponer matemáticamente en el producto del factor por su cuadrado:
Además, el binomio elevado a la 2 se trata de una identidad notable, por tanto, se puede resolver con la fórmula del cuadrado de una suma:
Ahora multiplicamos los dos paréntesis mediante la propiedad distributiva:
Y, por último, únicamente nos queda agrupar los términos que son semejantes:
De manera que queda verificada la fórmula de un binomio al cubo:
Lógicamente, para deducir la fórmula del binomio negativo al cubo se deben seguir los mismos pasos que acabamos de hacer pero empezando con el término cambiado de signo.
Por otra parte, la fórmula de un binomio al cubo también se puede demostrar mediante el triángulo de Pascal (o de Tartaglia). Por si no sabes en qué consiste este truco matemático, te dejamos este enlace donde se explica paso a paso. Además, podrás ver todas las aplicaciones que tiene y la peculiar historia que esconde este triángulo algebraico tan especial.
Ejercicios resueltos de binomios al cubo
Para que puedas practicar con la teoría que acabamos de ver sobre cómo calcular un binomio elevado a la 3, hemos preparado varios ejercicios resueltos paso a paso sobre el binomio al cubo.
¡Luego no olvides comentarnos que te ha parecido esta explicación! ¡Y también puedes preguntarnos cualquier duda que haya surgido! 👍👍👍
Ejercicio 1
Halla los siguientes binomios elevados al cubo:
Para hallar todas las identidades notables del problema simplemente debemos aplicar la fórmula del binomio al cubo, que depende de si se trata de una suma o una resta:
Ejercicio 2
Determina los siguientes binomios al cubo de dos cantidades aplicando la fórmula correspondiente:
Para calcular todos los productos notables del ejercicio debemos emplear la fórmula de una suma y de una resta elevada al cubo:
Los monomios del último binomio elevado al cubo tienen coeficientes fraccionarios, por lo que para resolverlo debemos usar las propiedades de las fracciones:

Buena explicación solamente una duda se que estos son al cubo pero tengo una duda con los elevados al cuadrado es un término (3x-5)²
Ya lo he hecho pero al final me da en un término uno negativo cuando debería de ser positivo (el término final de la ecuación final, lo sé por el binomio de Newton y el triángulo de Pascal si puedes ayudarme porfa🙏🏾
Hola Elliot,
Te tiene que dar un término negativo, así que es posible que lo tengas bien. Si quieres puedes compartir tus cálculos para poderte decir cuál es el fallo. A continuación te dejo con el ejercicio resuelto (recuerda que puedes practicar con ejercicios resueltos de este tipo en nuestro post del cuadrado de una diferencia):
Ten en cuenta que las fórmulas del binomio de Newton y del triángulo de Pascal cambian si el signo del medio es negativo. Puedes ver la explicación y las fórmulas buscando estos dos posts en nuestra página web.
Tengo la duda con el siguiente Binomio al cubo, pues si hago la multiplicacion no obtengo el mismo resultado : (-3 + 2m^2)^3 =
Por qué pasa eso? Que estoy haciendo mal?
Hola Gabo,
El resultado del ejercicio que propones es el siguiente:
Si quieres puedes escribir tus cálculos para ver qué está mal.