Producto de la suma por la diferencia (identidad notable)

En esta página encontrarás la fórmula del producto de la suma por la diferencia. Además, podrás ver ejemplos de cómo se aplica la fórmula de este tipo de identidad notable e, incluso, podrás practicar con ejercicios resueltos paso a paso.

¿Qué es el producto de la suma por la diferencia?

En matemáticas, el concepto de producto de la suma por la diferencia se refiere a una de las igualdades notables, también conocidas como identidades notables o productos notables.

En concreto, la expresión del producto de la suma por la diferencia es de la forma (a+b)·(a-b), donde (a+b) corresponde a la suma de dos términos diferentes, y (a-b) se trata de la diferencia de esos dos mismos términos.

Fórmula del producto de la suma por la diferencia

Ahora que ya sabemos la definición matemática del producto de la suma por la diferencia, veamos cuál es la fórmula que sirve para resolver este tipo de identidad notable:

producto de la suma por la diferencia

Por lo tanto, el producto de la suma por la diferencia de dos términos es igual a la diferencia de los cuadrados de dichos términos. Es decir, multiplicar la suma de dos términos distintos por la resta de esos dos mismos términos es equivalente a elevar al cuadrado cada uno de los 2 términos y restarlos.

Esto implica que las diferencias de cuadrados se pueden factorizar en productos de sumas por diferencias. Aunque ahora puede parecerte complicado, en la página enlazada explicamos un truco que permite factorizar este tipo de polinomios con dos simples pasos. Haz click y descubre cómo se hace.

Ejemplos de productos de sumas por diferencias

Una vez ya sabemos cuál es la fórmula del producto de la suma por la diferencia, a continuación vamos a ver varios ejemplos resueltos para que puedes entender mejor cómo se resuelve este tipo de igualdad notable.

Ejemplo 1

  • Calcula, aplicando la fórmula, el siguiente producto de la suma por la diferencia de dos términos distintos:

(x+2)\cdot (x-2)

La fórmula del producto de la suma por la diferencia es la siguiente:

(a+b)\cdot (a-b) =a^2-b^2

Así que lo primero que debemos hacer es identificar los valores de los parámetros a y b de la fórmula. En este caso a corresponde a la variable x y b corresponde al número 2.

\left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}

Y ahora que ya conocemos qué valores toman los parámetros a y b, podemos aplicar la fórmula del producto de la suma por la diferencia:

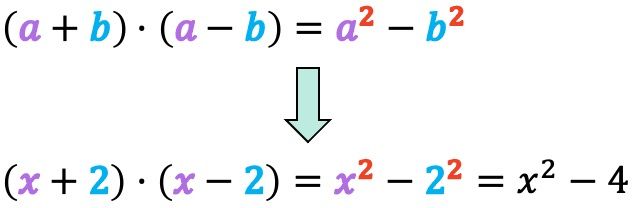
resolver cada suma por diferencia (x-2)(x+2)

Como puedes ver, el producto de una suma por una diferencia siempre dará como resultado un término negativo. Sin embargo, no debes confundir esto con la identidad notable del cuadrado de una resta. Si tienes dudas, te recomendamos que le eches un vistazo a cuál es la fórmula del cuadrado de una diferencia, donde también encontrarás cuáles son las diferencias entre estas dos identidades notables

Ejemplo 2

  • Halla, utilizando la fórmula, el siguiente producto de la suma por la diferencia de dos binomios:

(3x+5)\cdot (3x-5)

La fórmula del producto de la suma por la diferencia es la siguiente:

(a+b)\cdot (a-b) =a^2-b^2

Por lo tanto, en este caso a=3x y b=5. De manera que si aplicamos la fórmula de la suma por la diferencia obtenemos la siguiente expresión algebraica:

(3x+5)\cdot (3x-5) = (3x)^2-5^2 = 9x^2-25

Ejemplo 3

  • Resuelve con la fórmula el siguiente producto de la suma por la diferencia de dos monomios:

(4x-2y)\cdot (4x+2y)

Como la multiplicación tiene la propiedad conmutativa, multiplicar primero la diferencia y luego la suma de dos cantidades es lo mismo que multiplicar los mismos paréntesis a la inversa.

(4x-2y)\cdot (4x+2y) = (4x+2y)\cdot (4x-2y)

Por lo tanto, aunque en este caso el producto sea al revés, es decir, antes de la suma está la resta, el resultado sigue siendo el mismo de la fórmula:

(a+b)\cdot (a-b) =a^2-b^2

(a-b)\cdot (a+b) =a^2-b^2

De modo que en este problema a=4x y b=2y. Y cuando ya tenemos identificado el valor de cada incógnita podemos usar la fórmula para calcular el producto notable:

(4x-2y)\cdot (4x+2y)= (4x)^2-(2y)^2 = 16x^2-4y^2

Demostración de la fórmula de la suma por la diferencia

La fórmula que acabamos de estudiar de la suma por la diferencia se puede demostrar fácilmente.

Si empezamos desde el producto de una suma por una resta de dos términos cualesquiera:

(a+b)\cdot (a-b)

Simplemente tenemos que multiplicar el primer paréntesis por el segundo paréntesis mediante la propiedad distributiva:

\begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}

Y agrupando los términos semejantes llegamos a la siguiente expresión:

a^2 -ab+ba-b^2=a^2-b^2

Por lo que la fórmula del producto notable suma por diferencia queda demostrada:

(a+b)\cdot (a-b) =a^2-b^2

Ejercicios resueltos del producto de la suma por diferencia

A continuación hemos elaborado varios ejercicios resueltos paso a paso de sumas por diferencias para que puedas practicar. Los ejercicios están ordenados de menor a mayor dificultad, por lo que te recomendamos que empieces por el 1, sigas por el 2 y finalmente hagas el 3, que es el más difícil.

⬇⬇¡Recuerda también que puedes dejarnos cualquier duda que te surja en los comentarios!⬇⬇

Ejercicio 1

Resuelve los siguientes productos de sumas por diferencias:

\text{A)} \ (x+5)(x-5)

\text{B)} \ (2x+6)(2x-6)

\text{C)} \ (x+7)(x-7)

\text{D)} \ (x-4y)(x+4y)

\text{A)} \ \begin{array}{l}(x+5)(x-5) = \\[2ex] =x^2-5^2=\\[2ex] = \bm{x^2-25}\end{array}

 

\text{B)} \ \begin{array}{l}(2x+6)(2x-6) = \\[2ex] =(2x)^2-6^2=\\[2ex] = \bm{4x^2-36}\end{array}

 

\text{C)} \ \begin{array}{l}(x+7)(x-7) = \\[2ex] =x^2-7^2=\\[2ex] = \bm{x^2-49}\end{array}

 

\text{D)} \ \begin{array}{l}(x-4y)(x+4y) = \\[2ex] =(x+4y)(x-4y) =\\[2ex] =x^2-(4y)^2=\\[2ex] = \bm{x^2-16y^2}\end{array}

 

Ejercicio 2

Expresa las siguientes multiplicaciones como diferencias de cuadrados:

\text{A)} \ \left(x^2+10\right)\left(x^2-10\right)

\text{B)} \ \left(4x-5\right)\left(4x+5\right)

\text{C)} \ \left(8x^3+y^2\right)\left(8x^3-y^2\right)

\text{D)} \ \left(2x^3y+x^4y^2\right)\left(2x^3y-x^4y^2\right)

\text{A)} \ \begin{array}{l}\left(x^2+10\right)\left(x^2-10\right) = \\[2ex] =\left(x^2\right)^2-10^2=\\[2ex] = \bm{x^4-100}\end{array}

 

\text{B)} \ \begin{array}{l}\left(4x-5\right)\left(4x+5\right) = \\[2ex] =(4x)^2-5^2=\\[2ex] = \bm{16x^2-25}\end{array}

 

\text{C)} \ \begin{array}{l}\left(8x^3+y^2\right)\left(8x^3-y^2\right) = \\[2ex] =\left(8x^3\right)^2-\left(y^2\right)^2=\\[2ex] = \bm{64x^6-y^4}\end{array}

 

\text{D)} \ \begin{array}{l}\left(2x^3y+x^4y^2\right)\left(2x^3y-x^4y^2\right) = \\[2ex] =\left(2x^3y\right)^2-\left(x^4y^2\right)^2 =\\[2ex] = \bm{4x^6y^2-x^8y^4}\end{array}

 

Ejercicio 3

Resuelve las siguientes identidades notables:

\text{A)} \ \left(9x^3+\sqrt{5x}\right)\left(9x^3-\sqrt{5x}\right)

\text{B)} \ \displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right)

\text{C)} \ \left(6x^4+x^2+1\right)\left(6x^4-x^2-1\right)

Para solucionar la primera igualdad notable debes recordar que una raíz elevada al cuadrado se simplifica:

\text{A)} \ \begin{array}{l}\left(9x^3+\sqrt{5x}\right)\left(9x^3-\sqrt{5x}\right) = \\[2ex] =\left(9x^3\right)^2-\left(\sqrt{5x}\right)^2=\\[2ex] = \bm{81x^6-5x}\end{array}

 

Los 2 monomios de la segunda suma por una diferencia tienen coeficientes fraccionarios, con lo que debemos solucionar este ejercicio mediante las propiedades de las fracciones:

\text{B)} \ \begin{array}{l}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) = \\[4ex] \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2=\\[4ex] \displaystyle =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2=\\[4ex]\displaystyle = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{array}

 

Finalmente, la última igualdad notable es un poco especial porque dentro contiene otro producto notable (el cuadrado de la suma):

\text{C)} \ \begin{array}{l}\left(6x^4+x^2+1\right)\left(6x^4-x^2-1\right) = \\[2ex] = \left(6x^4+\left(x^2+1\right)\right)\left(6x^4-\left(x^2+1\right)\right)=\\[2ex]=\left(6x^4\right)^2-\left(x^2+1\right)^2=\\[2ex] =36x^8 - \left(x^4+2x^2+1\right)=\\[2ex] = \bm{36x^8 - x^4-2x^2-1}\end{array}

 

2 comentarios en “Producto de la suma por la diferencia (identidad notable)”

    1. Polinomios

      Hola Erick, buena pregunta.

      En este caso la fórmula es casi la misma, solo cambia el signo de los elementos del resultado, que es opuesto. De modo que el resultado del producto que propones sería:

      (6a^2+3b)\cdot (3b-6a^2)=(3b)^2-(6a^2)^2=9b^2-36a^4

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio