En esta página explicamos cuáles son las partes de un monomio (coeficiente, parte literal, grado,…) y cómo identificarlas fácilmente. Además, podrás ver ejemplos e incluso practicar con ejercicios resueltos paso a paso sobre las partes de un monomio.
Índice
¿Cuáles son las partes de un monomio?
Las partes de un monomio son:
- Coeficiente: es el número que multiplica a las variables (o letras) del monomio.
- Variable: son cada una de las letras que aparecen en el monomio.
- Parte literal: corresponde a todas las variables que forman el monomio junto con todos sus exponentes.
- Grado: es la suma de todos los exponentes de las variables del monomio.
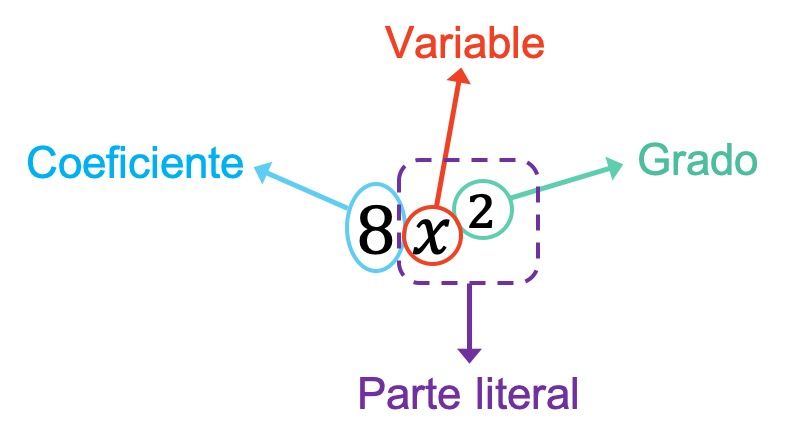
Como puedes ver en el ejemplo anterior, el coeficiente del monomio es 8 ya que es el número que está multiplicando a las variables. Además, en este caso el monomio solo tiene una variable, que es x. Por lo tanto, la parte literal del monomio está formada por esa variable más su exponente, es decir x2. Y, por último, el monomio es de segundo grado porque el único exponente que tiene es 2.
Por otro lado, una de las propiedades de las partes de un monomio es que cuando dos monomios tienen la misma parte literal se dice que son monomios semejantes. Puedes saber más sobre este tipo de monomios en la página enlazada, donde, entre otras cosas, se explica por qué son tan importantes para las matemáticas.
Ejemplos de partes de monomios
Para que acabes de entender completamente el concepto de las partes de un monomio, te dejamos con varios ejemplos:
Ejemplo 1
- Coeficiente del monomio:
- Variables del monomio:
(en este caso hay dos variables)
- Parte literal del monomio:
- Grado del monomio:
Ejemplo 2
- Coeficiente del monomio:
- Variables del monomio:
(en este caso hay tres variables)
- Parte literal del monomio:
- Grado del monomio:
Ten en cuenta que cuando no se pone el exponente de una variable significa que está elevada a uno y, por tanto, en realidad el exponente de esa variable es 1 y no 0. Por esta razón hemos sumado una unidad en el cálculo del grado de este monomio (3+1+4=8), ya que
Si estás más interesad@, en el siguiente enlace puedes ver más ejemplos de monomios. Aparte, podrás ver los diferentes tipos de monomios que hay, cómo se calcula el valor numérico de un monomio, y cuál es la diferencia entre un monomio y un polinomio.
Ejercicios resueltos de las partes de monomios
Finalmente, te proponemos varios ejercicios para que puedas comprobar que has entendido correctamente las diferentes definiciones de las partes de un monomio.
Ejercicio 1
¿Cuáles son todas las partes del siguiente monomio?
Coeficiente del monomio:
Variables del monomio:
Parte literal del monomio:
Grado del monomio:
Ejercicio 2
Identifica todos los elementos del siguiente monomio:
Coeficiente del monomio:
Variables del monomio:
Parte literal del monomio:
Grado del monomio:
Ejercicio 3
Determina las partes del siguiente monomio con una fracción:
Coeficiente del monomio:
Variables del monomio:
Parte literal del monomio:
Grado del monomio:
¡Perfecto! Si has llegado hasta aquí seguro que ya entiendes perfectamente todo sobre las partes de un monomio. Es por eso que ya estás preparad@ para pasar al siguiente nivel y aprender a cómo hacer operaciones con monomios. Aquí no solo verás cómo se calculan todos los tipos de operaciones con monomios que existen, sino que también verás cómo resolver operaciones combinadas con monomios y podrás practicar con ejercicios resueltos paso a paso.


me pueden ayudar con estos ejercicos por favor 🙏🙏🙏🙏🙏🙏🙏🙏
-15m^7,3x^4,a^3,4x^3,-7w^2x^6y^3
Claro Sofia,
Esperamos que te haya sido de ayuda y ahora entiendas mejor cómo se hace.
GRACIAS AMIGO/A PERO ME PUEDES ENSEÑAR POR FAVOR SOBRE ESTE TEMA
Hola Sofia de nuevo, tienes la explicación de cómo identificar todas las partes de un monomio arriba en la página, aquí en los comentarios te podemos resolver alguna duda concreta que tengas de cómo hacerlo. Te recomendamos que primero te leas la explicación y luego preguntes las dudas que te surjan en los comentarios, que las responderemos.
NO ENTIENDO POR QUE SALE ESAS RESPUESTAS PERO TENGO ESTE EJERCICIO 35B^3 4X^3
POR FAVOR AYUDAME SI 🙏🏾🙏🏾🙏🏾
Por supuesto, te resuelvo tu problema a continuación:
Identifica cuáles de las siguientes expresiones algebraicas son monomios, además indica cuál es su grado y su coeficiente.
a.- 3x elevada a la 3=
b.- 5x elevada a la -3=
c.- 3x+1=
d.- Raíz cuadrada de 2x=
e.- Menos 3 sobre x elevada a la 4=
como pinche resuelvo esto?
Hola Gerardo, un monomio es una expresión matemática formada por el producto de un número y de una o más letras (puedes buscar la definición de monomio en nuestra web). Y la diferencia entre un monomio y un polinomio es que un monomio es un único término, en cambio, un polinomio está formado por varios monomios.
Entonces, un monomio solamente puede tener un único término. Por tanto: es un monomio de grado 3 y su coeficiente es 3.
es un monomio de grado 3 y su coeficiente es 3. es un monomio de grado -3 y su coeficiente es 5.
es un monomio de grado -3 y su coeficiente es 5. no es un monomio, se trata de un polinomio.
no es un monomio, se trata de un polinomio. es un monomio de grado 1/2 y su coeficiente es
es un monomio de grado 1/2 y su coeficiente es 
 es un monomio de grado -4 y su coeficiente es -3.
es un monomio de grado -4 y su coeficiente es -3.
a)
b)
c)
d)
e)
Que sucedería si un exponente esta elevado a la 0, por ejemplo. 3 x^0 y^0 z^21. ¿Cual seria su coeficiente numérico, parte literal y su grado?
Buena pregunta Gregory.
Cualquier número elevado a 0 es igual a 1, por ejemplo 50=1. De modo que si el monomio tiene alguna incógnita elevada a cero en realidad esa incógnita es como un 1 y, por tanto, no afecta.
Por ejemplo, el monomio que propones en realidad sería:

Así que el coeficiente numérico, la parte literal y el grado de este monomio son:
– Coeficiente: 3
– Parte literal:
– Grado del monomio: 21
Espero haberte ayudado Gregory, cualquier duda me dices.
me ayudan a saber si este número 3x2y−6xy2+6 es, por favor
Binomio, grado 3, homogéneo
Trinomio, grado 3, heterogéneo
Binomio, grado 2, homogéneo
Trinomio, grado 2, heterogéneo
Hola Valeri,
El polinomio tiene 3 términos diferentes, por lo que es un trinomio. Además, el polinomio es de grado 3 pero no todos sus términos son del mismo grado, por tanto, es un polinomio heterogéneo. En conclusión, se trata de un trinomio de grado tres y heterogéneo.