Partes de un polinomio

Aquí encontrarás la explicación de cuáles son y cómo se llaman todas las partes de un polinomio (grado, variables, término independiente,…). Además, podrás ver varios ejemplos y practicar con ejercicios resueltos de las partes de un polinomio.

Pero antes de ver cuáles son todas las partes de un polinomio, repasemos rápidamente su definición matemática para poder entender bien el concepto: un polinomio es una expresión algebraica formada por la suma o la resta de monomios de diferente grado.

¿Cuáles son las partes de un polinomio?

La partes de un polinomio son:

• Términos: cada monomio que forma parte del polinomio.
• Coeficientes: los números que acompañan a cada término del polinomio.
• Grado: el mayor exponente al que está elevada la variable del polinomio.
• Variable: es la letra que tiene el polinomio.
• Término principal: es el término de mayor grado del polinomio.
• Término independiente: aquel término del polinomio que no contiene variable.
• Coeficiente principal: coeficiente del término principal del polinomio.

Cuando el polinomio tiene un sola variable, su grado es igual al exponente más grande de sus términos. Sin embargo, si el polinomio tiene dos o más variables, resulta más difícil averiguar su grado ya que se debe hacer una operación. Descubre cómo se hace haciendo click en el siguiente enlace del grado de un polinomio de dos variables (o más).

Cómo identificar las partes de un polinomio

Las partes o elementos de un polinomio se pueden hallar fácilmente de manera visual. Fíjate cómo se hace en el siguiente esquema:

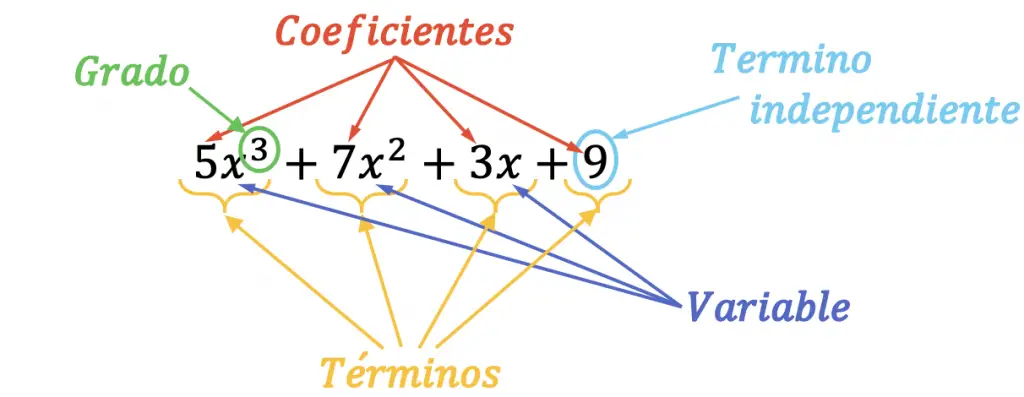
El polinomio anterior, que es de tercer grado, tiene todas sus partes señalizadas. Además, el término principal de dicho polinomio se trata de 5x³, porque es el monomio de mayor grado. Asimismo, el coeficiente principal del polinomio es 5, ya que es el coeficiente del término principal.

En este caso, el polinomio tiene una única variable y, por lo tanto, solamente tiene un tipo de grado. Pero debes saber que cuando el polinomio es multivariable hay que diferenciar entre el grado absoluto y el grado relativo de una variable. Puedes ver en qué consiste cada uno en el enlace qué te he dejado más arriba ⬆⬆ (grado de un polinomio de dos variables).

Ejemplos de las partes de un polinomio

Para acabar de comprender el significado de las partes de un polinomio y la función que cumplen, vamos a ver varios ejemplos de cómo se determinan las partes de cualquier tipo de polinomio:

Ejemplo 1

Identifica las partes del siguiente polinomio de segundo grado (de grado 2):

• Términos: 4x², -8x, 1
• Coeficientes: 4, -8, 1
• Grado: 2
• Variable: x
• Término principal: 4x²
• Término independiente: 1
• Coeficiente principal: 4

Por otro lado, cabe destacar que el polinomio de este ejemplo se llama trinomio. Puedes ver en qué consiste este tipo de polinomios en ejemplos de trinomios. Asimismo, puede que también te interese otro tipo de polinomio llamado binomio (es más fácil hacer algunas operaciones con él), puedes ver qué tiene de especial en ejemplos de binomios.

Ejemplo 2

Halla las partes del siguiente polinomio:

• Términos: y³, 9y², -5y, 3
• Coeficientes: 1, 9, -5, 3
• Grado: 3
• Variable: y
• Término principal: y³
• Término independiente: 3
• Coeficiente principal: 1

Como puedes comprobar en este ejemplo, cuando un monomio no tiene ningún número delante significa que su coeficiente es la unidad. Por eso el coeficiente principal de este polinomio es equivalente a 1.

Ejercicios resueltos de las partes de un polinomio

Para ayudarte a recordar los nombres de todas las partes de un polinomio, te hemos preparado varios ejercicios resueltos. Puedes preguntarnos cualquier duda sobre ellos en los comentarios. ⬇⬇

Ejercicio 1

Averigua todas las partes del siguiente polinomio:

El polinomio de este ejercicio no tiene término independiente ya que todos los términos están formados por, como mínimo, una variable (o letra).

Términos: 2x⁴, 6x², x

Coeficientes: 2, 6, 1

Grado: 4

Variable: x

Término principal: 2x⁴

Término independiente: no tiene

Coeficiente principal: 2

 

Ejercicio 2

Averigua todas las partes del siguiente polinomio:

El polinomio de este problema está compuesto por dos variables: x e y. Por tanto:

Términos: -7x⁴y², 3x⁴, -5y², xy, -10

Coeficientes: -7, 3, -5, 1, -10

Grado: 6

Variables: x, y

Término principal: -7x⁴y²

Término independiente: -10

Coeficiente principal: -7

Como puedes comprobar, para resolver polinomios como este debes saber cómo calcular el grado de un polinomio con más de una variable. Si aún no tienes del todo claro cómo se hace, te recomiendo que le eches un vistazo al enlace que hay arriba en el apartado de ¿Cuáles son las partes de un polinomio? (grado de un polinomio de dos variables). ⬆⬆ Allí encontrarás la explicación paso a paso junto con varios ejemplos.

 

Aunque es un concepto radicalmente distinto, si has llegado hasta aquí seguramente también te interese saber qué es la expresión polinómica de un número. Es algo que poca gente conoce pero que en realidad es muy útil.