▷ ¿Qué es un Trinomio Cuadrado Perfecto? (ejemplos)

En esta página explicamos en qué consiste un trinomio cuadrado perfecto y cómo se factoriza. Además, podrás ver varios ejemplos y practicar con ejercicios resueltos paso a paso del trinomio cuadrado perfecto.

Índice

¿Qué es un trinomio cuadrado perfecto?

Evidentemente, antes de ver el significado de un trinomio cuadrado perfecto debes saber qué son los trinomios, así que te recomiendo que le eches un vistazo a esta página enlazada (donde se explica detalladamente) antes de seguir.

Así pues, la definición de un trinomio cuadrado perfecto es la siguiente:

En matemáticas, un trinomio cuadrado perfecto, por brevedad también conocido como TCP, es el trinomio que se obtiene de elevar un binomio al cuadrado.

Por lo tanto, un trinomio cuadrado perfecto consiste en un polinomio con dos cuadrados perfectos y otro término que es el doble producto de las bases de esos cuadrados.

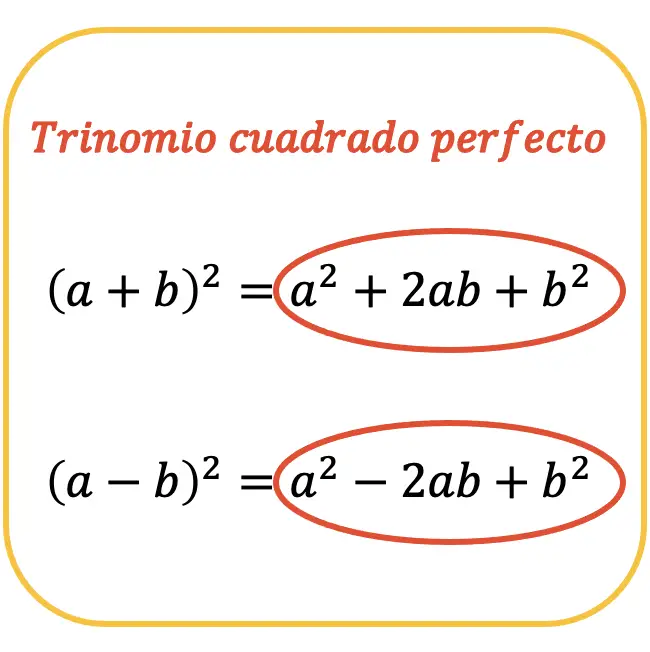
Como puedes ver en las dos fórmulas anteriores, el trinomio cuadrado perfecto se obtiene a partir de dos identidades notables (o productos notables), por eso es tan importante. En concreto, se halla un trinomio cuadrado perfecto cuando se resuelve el cuadrado de una suma o el cuadrado de una resta.

Ejemplos de trinomio cuadrado perfecto

Para acabar de entender el concepto del trinomio cuadrado perfecto, vamos a explicar 2 ejemplos paso a paso:

Ejemplo 1

$x^2+6x+9$

Este ejemplo es un trinomio cuadrado perfecto porque en su expresión algebraica hay dos cuadrados perfectos (es decir tienen una raíz cuadrada exacta), ya que $x^2$ y 9 son equivalentes a $x$ y 3 elevado a la dos respectivamente:

$(x)^2 = x^2$

$(3)^2 = 9$

Y, además, el último término restante del trinomio $(6x)$ se obtiene multiplicando las bases de los dos cuadrados anteriores entre sí y por 2:

$2\cdot x \cdot 3 = 6x$

De modo que toda la identidad notable completa en este ejercicio sería:

$(x+3)^2 =x^2+6x+9$

Ejemplo 2

$16x^2-40x+25$

Este otro ejemplo también es un trinomio cuadrado perfecto porque se cumplen las 3 condiciones necesarias: dos términos corresponden a dos cuadrados perfectos, y otro término es el resultado de multiplicar las bases de esos cuadrados entre sí y por 2.

$(4x)^2 = 16x^2$

$(5)^2 = 25$

$2\cdot 4x \cdot 5 =40x$

En este caso el trinomio cuadrado perfecto tiene un monomio negativo, por lo que corresponde al desarrollo de la igualdad notable de una diferencia al cuadrado:

$(4x-5)^2 = 16x^2-40x+25$

Cómo factorizar un trinomio cuadrado perfecto

En álgebra, un problema muy común es factorizar un trinomio cuadrado perfecto (TCP). Por si no sabes qué significa, factorizar un polinomio quiere decir transformar su expresión en un producto de factores.

Así pues, para poder factorizar este tipo de trinomio algebraico se deben cumplir las siguientes reglas:

El trinomio debe tener dos cuadrados perfectos, que llamaremos $a^2$ y $b^2.$
El tercer término restante del trinomio debe ser igual al doble producto de las bases de los dos cuadrados perfectos, que matemáticamente corresponde a la expresión $2\cdot a \cdot b.$
El trinomio factorizado será $(a+b)^2$ si todos los términos del trinomio cuadrado perfecto son positivos, de lo contrario, si el doble producto de las bases de los cuadrados tiene signo negativo, el trinomio factorizado será $(a-b)^2.$

Para acabar de entender el procedimiento, vamos a resolver un ejercicio paso a paso:

Factoriza el siguiente trinomio cuadrado perfecto:

$x^2-12x+36$

Lo primero que debemos hacer es identificar si el trinomio tiene dos elementos que son cuadrados perfectos, o dicho de otra forma, que su raíz cuadrada no da un número decimal. En este problema $x^2$ es el cuadrado de la variable $x$ y 36 es el cuadrado de 6:

$\sqrt{x^2} = x$

$\sqrt{36} = 6$

De modo que el trinomio efectivamente sí que tiene dos cuadrados perfectos.

En segundo lugar, tenemos que verificar si el término intermedio equivale al doble producto de las dos raíces calculadas en el paso anterior:

$2 \cdot x \cdot 6 = 12x$

También se cumple esta regla.

Entonces, se cumplen todas las condiciones. Por lo tanto, el trinomio cuadrado perfecto factorizado es el binomio formado por las dos raíces encontradas ( $x$ y el número 6) elevado al cuadrado:

$x^2-12x+36=(x-6)^2$

Como el término intermedio es negativo, también debemos poner un signo menos dentro del paréntesis. En cambio, si fuese positivo tendríamos que poner una suma:

$x^2+12x+36=(x+6)^2$

Lógicamente, la factorización es un procedimiento complicado así que, aparte de intentar hacer el ejercicio que tienes a continuación, te recomiendo que veas estos ejemplos de factorización de polinomios. En este enlace también explicamos un método que no solo sirve para factorizar trinomios, sino cualquier tipo de polinomio y, además, de manera rápida.

Ejercicios resueltos del trinomio cuadrado perfecto

Transforma los siguientes trinomios en binomios elevados al cuadrado aplicando la fórmula correspondiente:

$\text{A)} \ x^2+8x+16$

$\text{B)} \ x^2-14x+49$

$\text{C)} \ x^4-20x^2+100$

$\text{D)} \ 81x^2+90x+25$

$\text{E)} \ 64x^4-176x+121$

Ver solución

Para convertir un trinomio cuadrado perfecto en una potencia de un binomio elevado al cuadrado debemos utilizar las fórmulas de las identidades notables del cuadrado de una suma y del cuadrado de una diferencia, que son:

$(a+b)^2 = a^2+2ab+b^2$

$(a-b)^2 = a^2-2ab+b^2$

Por tanto:

$\text{A)} \ x^2+8x+16 = (x+4)^2$

$\text{B)} \ x^2-14x+49 = (x-7)^2$

$\text{C)} \ x^4-20x^2+100 = (x^2-10)^2$

$\text{D)} \ 81x^2+90x+25 = (9x+5)^2$

$\text{E)} \ 64x^4-176x+121 =\left( 8x^2-11)^2$

⬇⬇⬇ ¡Recuerda que puedes escribirnos cualquier duda que tengas abajo en los comentarios! ⬇⬇⬇

8 comentarios en “Trinomio cuadrado perfecto”

Sujey Sánchez Morales
02/09/2021 a las 05:38

Para empezar un trinomio es…un polinomio formado solamente por tres monomios.
Así que un trinomio cuadrado perfecto (TCP) es el trinomio que se obtiene de elevar un binomio al cuadrado o también un trinomio (polinomio de tres términos) tal que, dos de sus términos son cuadrados perfectos y el otro término es el doble producto de las bases de esos cuadrados.

Responder
1. Polinomios
  07/09/2021 a las 14:04
  
  Toda la razón Sujey, es lo que se intenta explicar en este post.
  
  Muchas gracias por tu aportación. 🙂
2. Juan
  20/01/2022 a las 12:36
  
  Hola espero que tengan un buen día, tengo una pregunta en la E) 64x⁴ – 176x + 127 y la respuesta (8x² – 11)² no coinciden por qué al desarrollar esta diferencia de binomios al cuadrado da como resultado 64x⁴ – 176x² + 127, está bien mi respuesta?
3. Polinomios
  27/01/2022 a las 18:53
  
  Buenas Juan,
  
  No entiendo la pregunta, ya que estás repitiendo la respuesta dos veces. Pero el resultado del ejercicio está bien.
Miri
15/11/2021 a las 18:51

¿Para que sirve? O para que se usa

Responder
1. Polinomios
  17/11/2021 a las 13:36
  
  Hola Miri,
  
  La fórmula del trinomio cuadrado perfecto sirve para factorizar un trinomio de este tipo rápidamente, lo que permite encontrar las raíces del polinomio de manera sencilla.
  
  De lo contrario, se tendría que aplicar el procedimiento de factorización de un polinomio, que es bastante más largo y tedioso. Para saber más, puedes consultar nuestros artículos de la factorización de polinomios y de las raíces de un polinomios.
cami
07/02/2023 a las 21:02

me sirvió mucho gracias

Responder
1. Polinomios
  11/02/2023 a las 13:14
  
  ¡Gracias a ti por comentar Cami!