▷ Cómo calcular un trinomio al cuadrado (fórmula y ejemplos)

En esta página explicamos cómo se resuelve el cuadrado de un trinomio (fórmula). Además, podrás ver varios ejemplos y practicar con ejercicios resueltos paso a paso de trinomios al cuadrado.

Índice

Fórmula de un trinomio al cuadrado

Lógicamente, para entender la fórmula del trinomio al cuadrado primero debes saber qué es un trinomio. Te dejo este enlace por si quieres repasarlo antes de seguir con la explicación.

Un trinomio elevado al cuadrado es igual al cuadrado del primer término, más el cuadrado del segundo término, más el cuadrado del tercer término, más el doble del primero por el segundo, más el doble del primero por el tercero, más el doble del segundo por el tercero.

cuadrado de un trinomio o trinomio al cuadrado

El cuadrado de un trinomio es tan importante porque se trata de un producto notable (o identidad notable), es decir, existe una fórmula matemática que permite calcular dicha operación de manera rápida. Haz click en el siguiente enlace para ver cuáles son todas las fórmulas de los productos notables.

Ejemplos de trinomios al cuadrado

Una vez hemos visto cuál es la fórmula de un trinomio al cuadrado, vamos a ver varios ejemplos de cómo calcular el cuadrado de un trinomio:

Ejemplo 1

Calcula la siguiente potencia de un trinomio elevado al cuadrado:

$\left(x^2+x+3\right)^2$

La fórmula del cuadrado de un trinomio es:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Por tanto, primero tenemos que identificar los valores de los parámetros $a,b$ y $c$ de la fórmula. En este ejercicio $a$ es $x^2,$ el coeficiente $b$ corresponde a la $x,$ y $c$ es el término independiente 3:

$\left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}$

Y cuando ya sabemos los valores, simplemente tenemos que sustituir dichos valores en la fórmula y hacer los cálculos:

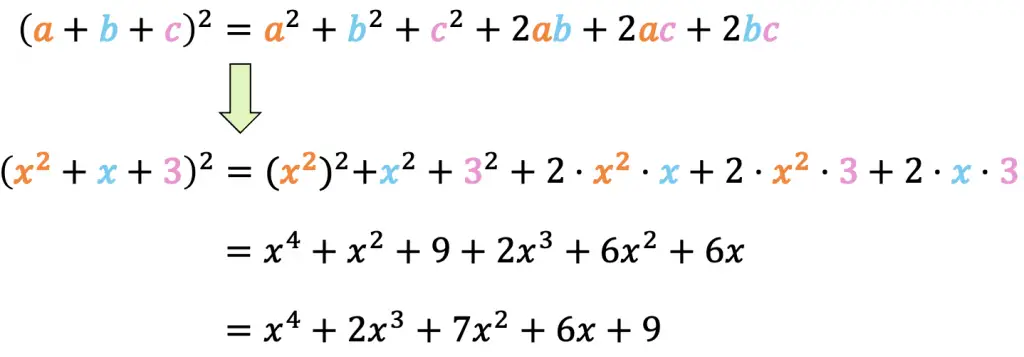
ejemplo de un trinomio elevado al cuadrado

Por otro lado, cabe destacar que un trinomio al cuadrado no es lo mismo que un trinomio cuadrado perfecto. Esto es un error habitual, ya que mucha gente se confunde con estos dos conceptos. Puedes ver las diferencias entre estos dos tipos de trinomios en el enlace de este párrafo.

Ejemplo 2

Halla el siguiente cuadrado de un trinomio:

$\left(x^2-2x+4\right)^2$

Para determinar esta potencia polinómica, debemos aplicar la fórmula de un trinomio elevado a la dos:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

En este problema, $a$ es equivalente a $x^2,$ $b$ corresponde al monomio negativo $-2x,$ y $c$ es el número 4:

$\left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2-2x+4\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=-2x \\[2ex] c=4 \end{array}$

De manera que sustituimos los valores hallados en la fórmula y resolvemos las operaciones resultantes:

$\begin{array}{l} \left(x^2-2x+4\right)^2 = \\[2ex] = \left(x^2\right)^2+(-2x)^2+4^2+2\cdot x^2 \cdot (-2x) + 2 \cdot x^2 \cdot 4 +2 \cdot (-2x) \cdot 4 = \\[2ex] = x^4+4x^2+16-4x^3 + 8x^2 -16x = \\[2ex] = x^4-4x^3+12x^2-16x+16 \end{array}$

Recuerda que la potencia con exponente par de una base negativa da como resultado un término positivo, por eso $(-2x)^2$ es igual a $4x^2.$

Ahora que ya has visto cómo se calcula el cuadrado de un trinomio, seguramente también te interese saber cómo se resuelve el producto de la suma por la diferencia de dos términos. De hecho, es una de las 3 identidades notables principales (más importantes). Puedes ver cuál es su fórmula y cómo se aplica en la página enlazada.

Demostración de la fórmula del cuadrado de un trinomio

Para acabar de entender el concepto de la potencia de un trinomio elevado al cuadrado, vamos a deducir la fórmula que acabamos de estudiar.

Partiendo de un trinomio cualquiera elevado a la 2:

$(a+b+c)^2$

La expresión algebraica anterior es equivalente a multiplicar el trinomio de dentro del paréntesis por sí mismo:

$(a+b+c)^2 = (a+b+c)(a+b+c)$

Ahora multiplicamos los dos trinomios:

$(a+b+c)(a+b+c)= a^2+ab+ac+ba+b^2+bc+ca+cb+c^2$

Por último, agrupamos los términos semejantes:

$a^2+ab+ac+ba+b^2+bc+ca+cb+c^2 = a^2+b^2+c^2+2ab+2ac+2bc$

Y de esta manera ya hemos llegado a la expresión de la fórmula, así que queda demostrada la fórmula del cuadrado de un trinomio:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

En nuestra web tenemos más demostraciones de identidades notables. Por ejemplo, puedes ver la demostración de la fórmula de una suma al cuadrado y de una diferencia al cuadrado. Además, en estos enlaces no solo verás sus demostraciones, sino también la interpretación geométrica de sus fórmulas, es decir, qué significan geométricamente estos tipos de identidades notables.

Ejercicios resueltos de trinomios al cuadrado

Resuelve los siguientes trinomios elevados al cuadrado:

$\text{A)} \ \left(x^2+x+5\right)^2$

$\text{B)} \ \left(x^2+3x-4\right)^2$

$\text{C)} \ \left(4x^2-6x+3\right)^2$

$\text{D)} \ \left(x^3-3x^2-9x\right)^2$

Ver solución

Para poder resolver todos los ejercicios tenemos que utilizar la fórmula del cuadrado de un trinomio, que es:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

$\text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}$

$\text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}$

$\text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}$

$\text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}$

Trinomio al cuadrado

Fórmula de un trinomio al cuadrado

Ejemplos de trinomios al cuadrado

Ejemplo 1

Ejemplo 2

Demostración de la fórmula del cuadrado de un trinomio

Ejercicios resueltos de trinomios al cuadrado

2 comentarios en “Trinomio al cuadrado”

Deja un comentario Cancelar respuesta